C++ 位运算异或操作符

位运算异或操作符也被称为 异或运算
使用符号 ‘^’ 表示
正如名称所示，它逐位操作操作数。
位运算异或操作符属于位运算符的一种。
在位运算异或操作符 (XOR) 中，需要两个操作数，这两个操作数通过异或符号 ‘^’ 分隔。
要确定在两个操作数应用异或操作后产生的输出或结果，需要遵循异或操作符的逻辑真值表。
异或真值表是使用异或操作符的适当逻辑构建的数学表格。
异或操作符背后使用的逻辑是：当异或操作应用于两个操作数的不同位时，结果总是产生 ‘1’， 如果异或操作应用于两个操作数的相同位，则结果产生输出 ‘0’。

异或操作 (XOR) 真值表

假设有两个操作数；第一个是 A，第二个是 B，由这两个操作数形成的输入的总组合数为4。通过使用下面的异或真值表，我们将确定相应的输出。结果将在 C 中保存，这里有 C = A ^ B。

在这个真值表中，我们以位的形式接受输入，即 0 和 1，输出也将以位的形式生成，即 0 和 1。

C++ 位运算异或操作符

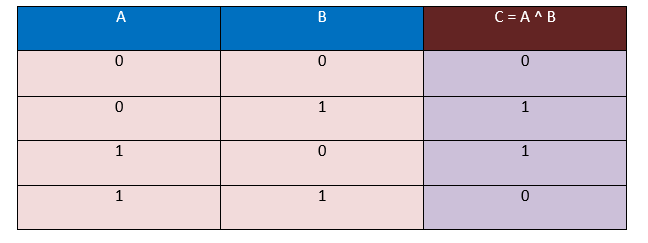
在上面的异或（XOR）真值表中，我们观察到当操作数A和B的值不同时，即（0, 1），（1, 0），输出始终为1。而当操作数A和B的值相同时，即（0, 0），（1, 1），输出始终为0。

同样地，我们可以用类似的方式为布尔值绘制真值表。

假设有两个操作数；第一个是A，第二个是B。由这两个操作数形成的输入的总组合数为4。通过使用下面的异或真值表，我们将确定相应的输出。结果将被记录在C中，即 C = A ^ B。

在此真值表中，我们以真值（True）和假值（False）的形式输入。输出也以真值（T）和假值（F）的形式生成。

C++ 位运算异或操作符

在上面的异或（XOR）真值表中，我们观察到当操作数A和B的值不同时，即（F，T），（T，F），结果始终为T。当操作数A和B的值相同时，即（F，F），（T，T），结果始终为F。

从上面的表格中，我们观察到 T（真）用1表示，F（假）用0表示。

解决任何给定问题的步骤-

问题中给出的操作数始终以十进制值给出。
首先，我们需要将操作数的值转换为 二进制 。
将操作数的值转换为二进制数后，将两个操作数叠放在一起。
请记住，在对它们应用异或（XOR）操作之前，请检查它们中的位数。
如果位数不匹配，则小操作数左端的额外0平衡位数。
最后，借助上面的真值表，逐个对操作数应用异或操作，每次取一位来应用异或操作。
最后，结果以输出的形式产生。
输出的形式将是二进制形式，现在将二进制形式转换为十进制形式，并记下结果值。

在C++中执行位异或（XOR）运算

让我们通过示例更详细地了解在C++中执行异或运算的过程-

示例1：找到整数值10和14的异或值。并解释它，写出在C++中执行的代码。

解决方案： 让我们考虑两个变量’a’和’b’，用来存储上述问题中给出的两个操作数，即10和14。

这里，a = 10，b = 14。

我们将按照以下步骤来找出给定两个操作数的异或值。

我们知道10和14是十进制形式的，在应用位异或运算时，需要将其转换为二进制形式。
二进制形式的’a’，即10是’1010’，二进制形式的’b’，即14是’1110’。
这里我们观察到a中的二进制位数是四位，b中的二进制位数也是四位；因此两个变量中的二进制位数是相同的，已经平衡，我们不需要添加更多的0来平衡它。
现在，将’b’中的二进制位放在’a’中的相应位置上。
最后，逐个对应的位应用异或操作，记录输出。
最后生成的输出是以二进制形式表示的，因为上面的问题是以十进制形式给出的，因此我们需要将结果转换为十进制形式。

解释：

a = 10（十进制形式）

b = 14（十进制形式）

现在，对于a XOR b，我们需要将a和b转换为二进制形式 –

a = 1010（二进制形式）

b = 1110（二进制形式）

现在，在a和b上应用XOR运算 –

a = 1010

b = 1110

-————–

a ^ b = 0100 （以二进制形式）

a ^ b的结果是0100，以二进制形式表示。

现在将结果转换为十进制形式，即4。

10 ^ 14 = 4

注意：使用上述XOR真值表，可以生成相应位的输出。

我们现在将在C++语言中对10和14应用位异或运算，并得到结果，即4。

以上示例的C++代码：

//************************ C++ Code ******************************
#include
using namespace std;
int main ()
{
    int a, b, c ;                     // Initializing integer variables to store data values
    cout << "Enter values of a and b -> " << endl ;
    cout << "a: " ;
    cin >> a ;                       // taking a as input from user
    cout << "b: " ;
    cin >> b ;                         // taking b as input from user
    c = a ^ b ;                      // storing XOR result of a and b in c
    cout << "Applying XOR operation on a and b: "<< endl ;
    cout << "a ^ b = " << c << endl ;                    // Printing the output

}

输出

C++ 位运算异或操作符

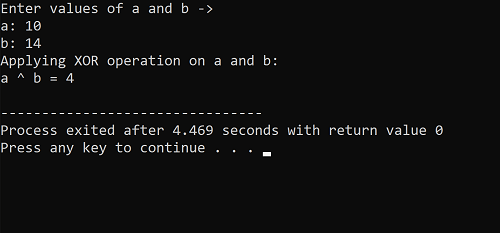
示例2：找到整数值3和15的异或运算。同时解释它并在C++中编写执行代码。

解决方案: 假设我们有两个变量’a’和’b’，用于存储上述问题中给定的两个操作数，即3和15。

这里，a = 3，b = 15。

我们将按照以下步骤找出给定两个操作数的异或结果。

我们知道3和15是十进制形式的，为了应用位异或运算，必须将其转换为二进制形式。
二进制形式的’a’，即3，为’11’；二进制形式的’b’，即15，为’1111’。
在这里，我们会发现a的二进制位数为2，b的二进制位数为4；因此，两个变量中的二进制位数不相同。因此，我们需要在较低的二进制数（即a）的左侧添加更多的0，以使其平衡。
平衡后，a的值为’0011’，b的值为’1111’。
现在，将’b’中的二进制位放在’a’的二进制位下面。
最后，逐位对应地应用异或操作，并记录输出。
最后生成的输出将以二进制形式呈现，因为以上问题给出的是十进制形式，所以我们需要将结果转换为十进制形式。

解释:

a = 3（以十进制形式）

b = 15（以十进制形式）

现在，对于一个异或b，我们需要将a和b转换为二进制形式 –

a = 0011（以二进制形式）

b = 1111（以二进制形式）

现在，在a和b上应用异或运算 –

a = 0011

b = 1111

-————–

a ^ b = 1100（以二进制形式）

a ^ b的结果为1100，以二进制形式表示。

现在将结果转换为十进制形式，即12。

3 ^ 15 = 12

注意：使用上述异或真值表，生成对应位的输出。

现在，我们将在C++语言中对3和15应用位异或运算，并获得结果，即12。

上述示例的C++代码：

//************************ C++ Code ******************************
#include
using namespace std;
int main ()
{
    int a, b, c ;                     // Initializing integer variables to store data values
    cout << "Enter values of a and b -> " << endl ;
    cout << "a: " ;
    cin >> a ;                       // taking a as input from user
    cout << "b: " ;
    cin >> b ;                         // taking b as input from user
    c = a ^ b ;                      // storing XOR result of a and b in c
    cout << "Applying XOR operation on a and b: "<< endl ;
    cout << "a ^ b = " << c << endl ;                    // Printing the output

}

输出

C++ 位运算异或操作符