C++ BigInt示例

在C或C++中，我们有不同类型的数据类型，如整数、长整数、浮点数、字符等。每种数据类型占用一定的内存空间。每种数据类型都有能够被占用的数字范围。

示例，一个整数占用4个字节的内存，因此我们可以使用整数表示从-2147483648到+2147463647之间的数字。

因此，如果我们想要一个十进制格式有22位或更多位数的整数，那么我们不能使用原始数据类型来存储它。为了解决这个问题，我们有BigInt数据类型可以进行以下操作：

对两个大整数求和
对两个大整数进行减法
对两个大整数进行乘法和除法
获取大整数的平方根
打印大整数或将整数转换为大整数

有很多应用程序中我们可以使用大整数数据类型，比如获取一个大数的Catalan或Fibonacci数或获取一个大整数的阶乘。我们将把这个大数以字符串格式存储，以便我们可以进行任何所需的操作。

1. 获取Fibonacci数

我们可以使用大整数数据类型得到一个巨大的Fibonacci数。

C++示例：

#include 
using namespace std;

class BigInt{
    string num;
public:
    BigInt(unsigned long long n = 0);
    BigInt(BigInt &);
    friend void divideByTwo(BigInt &a);
    friend int Length(const BigInt &);
    BigInt &operator=(const BigInt &);
    friend BigInt &operator+=(BigInt &, const BigInt &);
    friend ostream &operator<<(ostream &,const BigInt &);
    friend BigInt getNthFibNum(int n);
};

BigInt::BigInt(unsigned long long nr){
    do{
        num.push_back(nr % 10);
        nr /= 10;
    } while (nr);
}
BigInt::BigInt(BigInt & a){
    num = a.num;
}
int Length(const BigInt & a){
    return a.num.size();
}


BigInt &BigInt::operator=(const BigInt &a){
    num = a.num;
    return *this;
}



BigInt &operator+=(BigInt &a,const BigInt& b){
    int t = 0, s, i;
    int n = Length(a), m = Length(b);
    if(m > n)
        a.num.append(m - n, 0);
    n = Length(a);
    for (i = 0; i < n;i++){
        if(i < m)
            s = (a.num[i] + b.num[i]) + t;
        else
            s = a.num[i] + t;
        t = s / 10;
        a.num[i] = (s % 10);
    }
    if(t)
        a.num.push_back(t);
    return a;
}
BigInt operator+(const BigInt &a, const BigInt &b){
    BigInt temp;
    temp = a;
    temp += b;
    return temp;
}





void divideByTwo(BigInt & a){
    int add = 0;
    for (int i = a.num.size() - 1; i >= 0;i--){
        int digit = (a.num[i] >> 1) + add;
        add = ((a.num[i] & 1) * 5);
        a.num[i] = digit;
    }
    while(a.num.size() > 1 && !a.num.back())
        a.num.pop_back();
}

BigInt getNthFibNum(int n){
    BigInt a(1), b(1), c;
    if(!n)
        return c;
    n--;
    while(n--){
        c = a + b;
        b = a;
        a = c;
    }
    return b;
}


ostream &operator<<(ostream &out,const BigInt &a){
    for (int i = a.num.size() - 1; i >= 0;i--)
        cout << (short)a.num[i];
    return cout;
}
int main(){
    for (int i = 0; i <= 100; i++) {
        BigInt Fib;
        Fib = getNthFibNum(i);
        cout << "Fibonacci number at " << i << " = " << Fib<<'\n';
    }
}

输出：

C++ BigInt示例

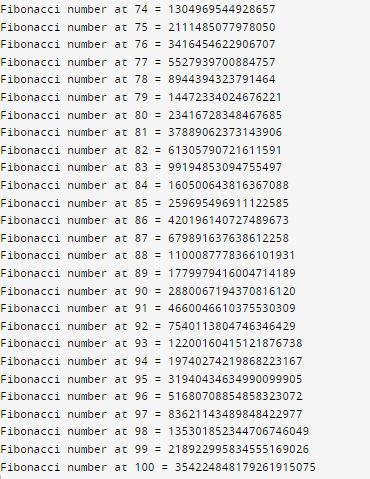
解释:

我们可以得到第100个斐波那契数，这个数非常大，但是借助一个大整数，我们可以实现这个目标。

2. 获取一个大数的阶乘

C++示例：

#include 

using namespace std;

class BigInt{
    string num;
public:

    BigInt(unsigned long long n = 0);
    friend void divideByTwo(BigInt &a);
    friend bool Null(const BigInt &);
    BigInt &operator=(const BigInt &);
    friend BigInt &operator*=(BigInt &, const BigInt &);
    friend ostream &operator<<(ostream &,const BigInt &);
    friend BigInt getFactorial(int n);
};

BigInt::BigInt(unsigned long long nr){
    do{
        num.push_back(nr % 10);
        nr /= 10;
    } while (nr);
}


bool Null(const BigInt& a){
    if(a.num.size() == 1 && a.num[0] == 0)
        return true;
    return false;
}

BigInt &BigInt::operator=(const BigInt &a){
    num = a.num;
    return *this;
}

BigInt &operator*=(BigInt &a, const BigInt &b)
{
    if(Null(a) || Null(b)){
        a = BigInt();
        return a;
    }
    int n = a.num.size(), m = b.num.size();
    vector v(n + m, 0);
    for (int i = 0; i < n;i++)
        for (int j = 0; j < m;j++){
            v[i + j] += (a.num[i] ) * (b.num[j]);
        }
    n += m;
    a.num.resize(v.size());
    for (int s, i = 0, t = 0; i < n; i++)
    {
        s = t + v[i];
        v[i] = s % 10;
        t = s / 10;
        a.num[i] = v[i] ;
    }
    for (int i = n - 1; i >= 1 && !v[i];i--)
            a.num.pop_back();
    return a;
}

void divideByTwo(BigInt & a){
    int add = 0;
    for (int i = a.num.size() - 1; i >= 0;i--){
        int digit = (a.num[i] >> 1) + add;
        add = ((a.num[i] & 1) * 5);
        a.num[i] = digit;
    }
    while(a.num.size() > 1 && !a.num.back())
        a.num.pop_back();
}

BigInt getFactorial(int n){
    BigInt f(1);
    for (int i = 2; i <= n;i++)
        f *= i;
    return f;
}

ostream &operator<<(ostream &out,const BigInt &a){
    for (int i = a.num.size() - 1; i >= 0;i--)
        cout << (short)a.num[i];
    return cout;
}


int main()
{
    for (int i = 0; i <= 100; i++) {
        BigInt fact;
        fact = getFactorial(i);
        cout << "Factorial of "
            << i << " = ";
        cout << fact << '\n';
}
}

输出：

C++ BigInt示例