C++ STL中的向量数组
什么是数组
数组是线性数据结构,以线性的方式存储相同数据类型的数据或值。存储在数组中的值或数据以连续的顺序分配内存。
根据其维度,数组可以有不同的类型,如一维数组、二维数组、三维数组等。
多维数组也被称为数组。
在C或C++中,要声明数组,首先我们必须告诉元素的数量或我们需要的内存。然后我们可以填充声明的数组中的值。
语法:
data_type array_name[number_of_elements];
什么是向量
向量也是一种数据结构,以与数组相同的方式存储值,但它们具有自动调整大小的能力。由于自动增加自身的大小,向量也被称为动态数组。
在数组中,在声明时,我们必须告诉数组要放入的元素数量,但在向量的情况下,我们不需要声明元素的数量,因为它可以在完全填充时增加其大小。
向量在C++的STL(Standard Template Library)中定义,因此要使用向量,我们必须将STL库导入程序文件中。
由于向量在STL(Standard Template Library)中定义,所以它具有许多内置函数,用于在任何索引处插入,删除或修改元素,无论是在起始端,结束端还是在任何位置。
示例:size(),capacity(),push_back()等。
以下是向量中使用的内置函数:
- size() :这个函数返回向量中存在的元素数量。
- capacity() :这个函数返回向量中的元素数量或容量。
- empty() :它返回当前向量是否为空或不为空。
- push_back() :借助这个函数,我们可以在向量的后面插入一个元素。
- pop_back() :借助这个函数,我们可以从向量的后面移除或删除元素。
- insert() :借助这个函数,我们可以在向量的任何指定位置插入元素。
- erase() :借助这个函数,我们可以从向量的特定位置删除元素。
语法:
vector vector_name;
向量数组
向量数组基本上是二维矩阵或数组,其中列数可以是任意值,但行数是固定的。
由于每一行代表一个向量,而一个向量可以有任意数量的元素,因此每一行可以有任意数量的列。
可以看起来像这样:
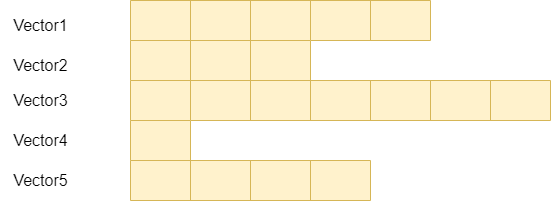
语法:
vector<data_type> array_name[array_size];
语法类似于数组声明,但数组的数据类型是向量。
C++示例:
#include <iostream>
#include<vector>
using namespace std;
int main() {
int n =5;// number of rows is 5
vector<int> vc[n];
//inserting in the first row
vc[0].push_back(1);
vc[0].push_back(2);
vc[0].push_back(3);
vc[0].push_back(4);
vc[0].push_back(5);
//inserting in the second row
vc[1].push_back(6);
vc[1].push_back(7);
vc[1].push_back(8);
//inserting in the third row
vc[2].push_back(9);
vc[2].push_back(10);
vc[2].push_back(11);
vc[2].push_back(12);
//inserting in the fourth row
vc[3].push_back(13);
vc[3].push_back(14);
//inserting in the fifth row
vc[4].push_back(15);
for(int i=0;i<n;i++){
cout<<"number of column in row number "<<i+1<<" is "<<vc[i].size()<<endl;
for(int j=0;j<vc[i].size();j++){
cout<<vc[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
输出:
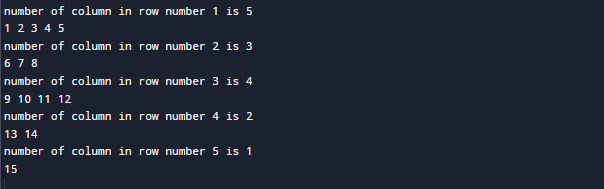
解释:
在上面的代码中,我们创建了大小为5的向量数组,这意味着行的数量是固定的,并且它们由数组大小为5表示。由于我们有一个大小为五的数组,这也意味着我们将有五个向量,它们可以具有不同的大小。
在第一个向量中,我们放入了五个元素,它们分别是:1、2、3、4、5。
在第二个向量中,我们放入了三个元素,它们分别是:6、7、8。
在第三个向量中,我们放入了四个元素,它们分别是:9、10、11、12。
在第四个向量中,我们放入了两个元素,它们分别是:13和14。
在第五个向量中,我们放入了一个元素,它是15。
现在,我们使用两个循环来打印我们的向量数组的所有元素。
外部循环将计算行的数量,因此它将运行n次,内部循环将运行每个向量中的元素数量次。
 极客笔记
极客笔记