C++ 哈希程序与链式处理

哈希表链式处理到底是什么

链式处理是一种哈希表中避免碰撞的技术。

碰撞发生在哈希表中的两个键被哈希到相同索引的情况下。碰撞是一个问题，因为哈希表中的每个槽位只能容纳一个元素。

C++ 哈希程序与链式处理

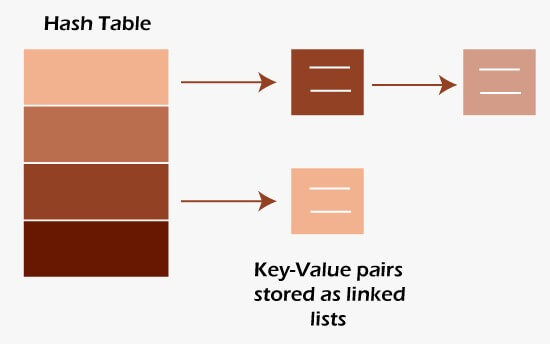
链接法

链接法中的哈希表是一个链表数组，每个索引都有自己的链表。

将到达相同索引的所有键值对存储在该索引的链表中。

链接法的优点

哈希表中的插入总是通过链接进行，因为链表允许在常数时间内插入。
链接哈希表在有足够空间的情况下可以理论上无限增长。
链接哈希表永远不需要重新调整大小。

链接法的实现

让我们编写一个哈希函数，以确保我们的哈希表具有“N”个桶。

要将节点添加到哈希表中，我们必须首先确定给定键的哈希索引。也可以使用哈希函数进行计算。

示例：hashIndex = key％noOfBuckets

插入： 移动到对应于上面计算的哈希索引的桶，并在列表末尾插入新节点。

删除： 要从哈希表中删除节点，计算密钥的哈希索引，移动到对应于计算的哈希索引的桶，搜索当前桶中的列表以查找具有给定键的节点，并将其删除（如果找到）。

算法

用于插入：

Begin
   Declare Function Insert(int k, int v)
      int hash_v = HashFunc(k)
      HashTableEntry* p = NULL
      HashTableEntry* en = ht[hash_v]
      while (en!= NULL)
         p = en
         en= en->n
      if (en == NULL)
         en = new HashTableEntry(k, v)
         if (p == NULL)
            ht[hash_v] = en
         else
            p->n= en
      else
         en->v = v
End.

删除：

Begin
   Declare Function Remove(int k)
      int hash_v = HashFunc(k)
      HashTableEntry* en = ht[hash_v]
      HashTableEntry* p= NULL
      if (en == NULL or en->k != k)
         Print "No Element found at key"
         return
      while (en->n != NULL)
         p = en
         en = en->n
      if (p != NULL)
         p->n = en->n
      delete en
         Print "Element Deleted"
End.

搜索：

Begin
   Declare function SearchKey(int k)
      int hash_v = HashFunc(k)
      bool flag = false
      HashTableEntry* en = ht[hash_v]
      if (en != NULL)
         while (en != NULL)
            if (en->k == k)
               flag = true
            if (flag)
               Print "Element found at key"
               Print en->v
            en = en->n
      if (!flag)
         Print "No Element found at key"
End.

代码

#include 
const int T_S = 200;
using namespace std;
struct HashTableEntry {
   int v, k;
   HashTableEntry *n;
   HashTableEntry *p;
   HashTableEntry(int k, int v) {
      this->k = k;
      this->v = v;
      this->n = NULL;
   }
};
class HashMapTable {
   public:
      HashTableEntry **ht, **top;
      HashMapTable() {
         ht = new HashTableEntry*[T_S];
         for (int i = 0; i < T_S; i++)
            ht[i] = NULL;
      }
      int HashFunc(int key) {
         return key % T_S;
      }
      void Insert(int k, int v) {
         int hash_v = HashFunc(k);
         HashTableEntry* p = NULL;
         HashTableEntry* en = ht[hash_v];
         while (en!= NULL) {
            p = en;
            en = en->n;
         }
         if (en == NULL) {
            en = new HashTableEntry(k, v);
            if (p == NULL) {
               ht[hash_v] = en;
            } else {
               p->n = en;
            }
         } else {
            en->v = v;
         }
      }
      void Remove(int k) {
         int hash_v = HashFunc(k);
         HashTableEntry* en = ht[hash_v];
         HashTableEntry* p = NULL;
         if (en == NULL || en->k != k) {
            cout<<"No Element found at key "<n != NULL) {
            p = en;
            en = en->n;
         }
         if (p != NULL) {
            p->n = en->n;
         }
         delete en;
         cout<<"Element Deleted"<k == k) {
                  flag = true;
               }
               if (flag) {
                  cout<<"Element found at key "<v<n;
            }
         }
         if (!flag)
            cout<<"No Element found at key "<>c;
      switch(c) {
         case 1:
            cout<<"Enter element to be inserted: ";
            cin>>v;
            cout<<"Enter key at which element to be inserted: ";
            cin>>k;
            hash.Insert(k, v);
         break;
         case 2:
            cout<<"Enter key of the element to be searched: ";
            cin>>k;
            hash.SearchKey(k);
         break;
         case 3:
            cout<<"Enter key of the element to be deleted: ";
            cin>>k;
            hash.Remove(k);
         break;
         case 4:
            exit(1);
         default:
            cout<<"\nEnter correct option\n";
      }
   }
   return 0;
}

输出

1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 1
Enter element to be inserted: 2
Enter key at which element to be inserted: 1
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 1
Enter element to be inserted: 3
Enter key at which element to be inserted: 4
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 1
Enter element to be inserted: 7
Enter key at which element to be inserted: 6
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 1
Enter element to be inserted: 8
Enter key at which element to be inserted: 9
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 2
Enter key of the element to be searched: 6
Element found at key 6: 7
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 2
Enter key of the element to be searched: 7
No Element found at key 7
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 3
Enter key of the element to be deleted: 9
Element Deleted
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. ExitC
Enter your choice: 4