Python 旋转图片程序|极客笔记

Python 旋转图片程序

在本教程中，我们将编写Python程序来解决旋转图片（矩阵）的问题。这是一个与矩阵相关的问题。让我们了解一下问题陈述。

问题陈述

一个nxn的二维矩阵表示一张图片。我们需要将图片顺时针旋转90度。我们需要使用就地操作来执行此操作，这意味着我们不需要另一个二维矩阵来进行旋转。旋转后，图片将如下所示。

示例 –

Python 旋转图片程序

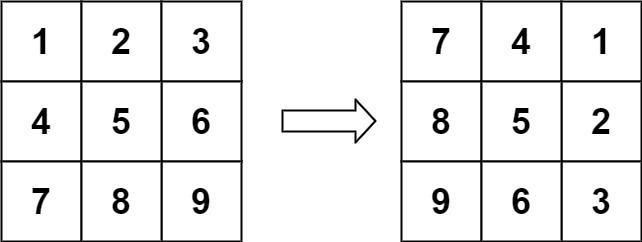
示例1

Input
matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output:
[[7,4,1],[8,5,2],[9,6,3]]

示例2

Input: 
matrix = [[5, 1, 9, 11], [2, 4, 8, 10], [13, 3, 6, 7], [15, 14, 12, 16]]
Output: 
[[15, 13, 2, 5], [14, 3, 4, 1], [12, 6, 8, 9], [16, 7, 10, 11]]

示例3

Input: matrix = [[1]]
Output: [[1]]

我们应该遵循以下约束条件 –

  • n == matrix.length == matrix[i].length
  • 1 <= n <= 20
  • -1000 <= matrix[i][j] <= 1000

解决方案1

我们将实现以下解决方案。

首先，获取矩阵的行数和列数。
迭代内循环和外循环，并转置矩阵。
反转转置后的矩阵。

让我们看下面的代码。

示例

def rotate(matrix):
    """
    :type matrix: List[List[int]]
    :rtype: None Do not return anything, modify matrix in-place instead.
    """
  if(matrix==None or len(matrix) == 0 or len(matrix[0]) == 0):return
    for row in range(len(matrix)):
        for col in range(row):
            matrix[row][col], matrix[col][row] = matrix[col][row], matrix[row][col]
    for i,row in enumerate(matrix):
        matrix[i]=row[::-1] 
    return matrix
mat = [[1,2,3],[4,5,6],[7,8,9]]
print('The input matrix is:', mat)
print("The matrix after rotation: ", rotate(mat))

输出:

The input matrix is: [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
The matrix after rotation:  [[7, 4, 1], [8, 5, 2], [9, 6, 3]]

解释 –

在上面的代码中，我们创建了一个方法，它接受一个要旋转的矩阵。我们迭代了外部循环，它将迭代矩阵的每一行，而外部循环又迭代每一行的列。我们在内部循环中将矩阵的行变为列，列变为行。如果我们打印转置后的矩阵，它将如下所示。

for row in range(len(matrix)):
        for col in range(row):
            matrix[row][col], matrix[col][row] = matrix[col][row], matrix[row][col]
print(matrix)

这将输出以下结果 –

[[1, 4, 7], [2, 5, 8], [3, 6, 9]]

如果我们仔细观察转置矩阵，我们距离得到期望的输出只差一步。我们只需要逆转每一行。因此，我们使用 enumerate() 函数逆转了矩阵的每一行。

for i,row in enumerate(matrix):
        matrix[i]=row[::-1] 
        print(i, row)

它将会给出以下输出 –

0 [1, 4, 7]
1 [2, 5, 8]
2 [3, 6, 9]

在下一行中，我们反转了行并返回了矩阵。

让我们了解另一种解决方案。

解决方案2

在此解决方案中，我们将

上下交换行，例如有n行：交换第1行和第n行，第2行和第(n-1)行，依此类推。
然后找到结果矩阵的转置。

让我们了解以下示例。

示例

def rotate(matrix):
        if(matrix==None or len(matrix) == 0 or len(matrix[0]) == 0):return
        rows = len(matrix)
        cols = len(matrix[0])

        first,last = 0,rows-1

while(first

输出：

The input matrix is: [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
[[7, 8, 9], [4, 5, 6], [1, 2, 3]]
The matrix after rotation:  [[7, 4, 1], [8, 5, 2], [9, 6, 3]]