操作系统餐桌哲学家问题

餐桌哲学家问题是经典的同步问题，它描述了五位哲学家坐在一个圆桌旁，他们的任务是交替思考和进食。桌子的中央摆放着一碗面条，每位哲学家旁边有五根筷子。为了进食，哲学家需要同时拥有右手和左手的筷子。只有当哲学家的左右两侧的筷子都可用时，他才能进食。如果哲学家的左右两侧筷子都不可用，那么他会放下一根（左手或右手）筷子，重新开始思考。

餐桌哲学家问题展示了一类大型并发控制问题，因此它是一个经典的同步问题。

操作系统餐桌哲学家问题

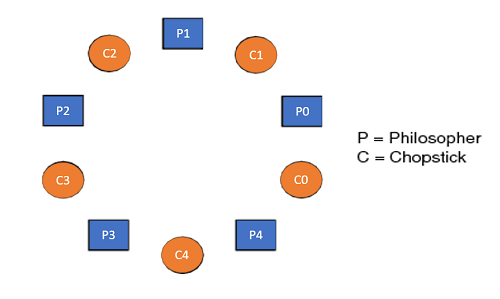
五位哲学家围坐在桌子旁

餐厅哲学家问题 - 让我们通过下面的代码来理解餐厅哲学家问题，我们使用图1作为参考，以便您准确理解问题。五位哲学家分别表示为P0、P1、P2、P3和P4，五把筷子分别为C0、C1、C2、C3和C4。

操作系统餐桌哲学家问题

Void Philosopher
 {
 while(1)
  {
   take_chopstick[i];
   take_chopstick[ (i+1) % 5] ;
   . .
   . EATING THE NOODLE
   .
   put_chopstick[i] );
   put_chopstick[ (i+1) % 5] ;
   .
   . THINKING
  }
}

让我们讨论上面的代码：

假设哲学家P0想要进餐，它将进入Philosopher（）函数，并执行 take_chopstick[i]; 通过这样做，它持有 C0筷子 之后，它执行 take_chopstick [（i + 1）％ 5]; 通过这样做，它持有 C1筷子 （因为i = 0，因此（0 + 1）％5 = 1）

类似地，假设现在哲学家P1想要进餐，它将进入Philosopher（）函数，并执行 take_chopstick [i]; 通过这样做，它持有 C1筷子 之后，它执行 take_chopstick [（i + 1）％5]; 通过这样做，它持有 C2筷子 （因为i = 1，所以（1 + 1）％5 = 2）

但实际上，筷子C1不可用，因为它已经被哲学家P0拿走了，因此上述代码会产生问题并产生竞争条件。

哲学家就餐问题的解决方案

我们使用一个信号量来表示一个筷子，这真正是哲学家进餐问题的解决方案。等待和信号操作将用于哲学家进餐问题的解决方案，对于拿起一个筷子，可以执行等待操作，而对于释放一个筷子，可以执行信号操作。

信号量：信号量是一个整数变量S，除了初始化外，只有两个标准原子操作可以访问它-等待（wait）和信号（signal），它们的定义如下：

1. wait( S )
{
while( S <= 0) ;
S--;
}

2. signal( S )
{
S++;
}

从以上对wait的定义来看，很明显如果S的值小于等于0，则会进入无限循环（因为while循环后面有一个分号;）。而信号的作用是增加S的值。

筷子的结构是一个信号量的数组，表示如下-

semaphore C[5];

最初时，信号量C0、C1、C2、C3和C4的每个元素都被初始化为1，因为筷子在桌子上，没有被任何哲学家拿起。

让我们通过使用信号量操作的等待和发信号的方法修改上述的餐桌哲学家问题代码，修改后的代码如下：

void Philosopher
 {
 while(1)
  {
   Wait( take_chopstickC[i] );
   Wait( take_chopstickC[(i+1) % 5] ) ;
   . .
   . EATING THE NOODLE
   .
   Signal( put_chopstickC[i] );
   Signal( put_chopstickC[ (i+1) % 5] ) ;
   .
   . THINKING
  }
}

在上述代码中，首先在take_chopstickC[i]和take_chopstickC [(i+1) % 5]上执行等待操作。这表示哲学家i从左边和右边拿起了筷子。然后执行进食函数。

当哲学家i完成用餐后，对take_chopstickC[i]和take_chopstickC [(i+1) % 5]执行信号操作。这表示哲学家i已经吃完并放下了左右两个筷子。最后，哲学家重新开始思考。

让我们理解一下上述代码如何解决餐桌哲学家问题

假设i的值为0（初始值），假设哲学家P0想要进食，它将进入Philosopher（）函数，并执行 等待（take_chopstickC [i]）; 通过这样做，它占有了 C0筷子 并将信号量C0减少为0 ，然后执行 等待（take_chopstickC [(i+1) % 5]）; 通过这样做，它占有了 C1筷子 （因为i = 0，所以（0 + 1）% 5 = 1），并将信号量C1减少为0

同样，假设现在哲学家P1想要进食，它将进入Philosopher（）函数，并执行 等待（take_chopstickC [i]）; 通过这样做，它将尝试占有 C1筷子 但无法做到，因为哲学家P0已经将信号量C1设置为0，所以它将进入无限循环，因此哲学家P1将无法拿起筷子C1，而如果哲学家P2想要进食，它将进入Philosopher（）函数，并执行 等待（take_chopstickC [i]）; 通过这样做，它占有了 C2筷子 并将信号量C2减少为0，之后它执行 等待（take_chopstickC [(i+1) % 5]）; 通过这样做，它占有了 C3筷子 （因为i = 2，所以（2 + 1）% 5 = 3），并将信号量C3减少为0。

因此，上述代码为餐桌哲学家问题提供了解决方案，如果哲学家的直接左边和右边的筷子都可用，则哲学家才能进食，否则哲学家需要等待。同时，两个独立的哲学家可以同时进食（即哲学家 **P0和P2，P1和P3 & P2和P4 ** 可以同时进食，因为它们都是独立的进程，并且它们遵循了餐桌哲学家问题的约束条件）

餐桌哲学家问题上述解决方案的缺点

从上面的哲学家就餐问题的解决方案可以得出，相邻的两位哲学家不能在同一时间吃饭。上述解决方案的缺点是可能会导致死锁。如果所有的哲学家同时拿起他们的左手筷子，就会出现死锁的情况，而且没有哲学家能够进食。

为了避免死锁，以下是一些解决方案：

桌子上哲学家的最大数量不应超过四个，这种情况下，筷子C4将空出给哲学家P3，因此P3将开始进食，吃完之后，他将放下他的两只筷子C3和C4，即信号量C3和C4现在增加到1。现在持有筷子C2的哲学家P2也将可以拿到筷子C3，因此他吃完之后也会放下筷子，让其他哲学家可以进食。
一个偶数位置的哲学家应先拿起右边的筷子，然后再拿起左边的筷子，而奇数位置的哲学家应先拿起左边的筷子，然后再拿起右边的筷子。
只有当左右两只筷子都同时可用时，哲学家才可以拿起他们的筷子。
所有四位起始的哲学家（P0、P1、P2和P3）应先拿起左手的筷子，然后拿起右手的筷子，而最后一位哲学家P4应先拿起右手的筷子，然后再拿起左手的筷子。这将强迫P4先持有他的右手筷子，因为P4的右手筷子是C0，而P0已经持有了它并且将其值设为0，即C0已经为0，因此P4将陷入无限循环而筷子C4将保持空闲。因此，哲学家P3拥有左手的筷子C3和右手的筷子C4，因此它将开始进食，并在吃完后放下两只筷子，让其他人来进食，这样消除了死锁问题。

问题的设计是为了说明避免死锁的挑战，系统的死锁状态是系统无法进行任何进展的状态。考虑一种方案，每个哲学家被要求按照以下方式行事：