操作系统 RR循环调度示例

在下面的示例中，有六个进程，分别命名为P1、P2、P3、P4、P5和P6。它们的到达时间和执行时间在下表中给出。系统的时间片大小为4个单位。

Process ID	Arrival Time	Burst Time
1	0	5
2	1	6
3	2	3
4	3	1
5	4	5
6	6	4

根据算法的要求，我们必须维护就绪队列和甘特图。每次调度后，这两个数据结构的结构都会发生变化。

就绪队列

最初，在时间0，进程P1到达，它将被调度为时间片4个单位。因此，就绪队列开始时只有一个进程P1，CPU执行时间为5个单位。

P1
5

甘特图

P1首先执行4个单位。

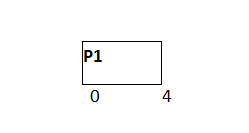
就绪队列

与此同时，在执行P1的同时，另外四个进程P2、P3、P4和P5到达了就绪队列。P1尚未完成，它还需要1个单位的时间，因此它也将被添加回就绪队列中。

P2	P3	P4	P5	P1
6	3	1	5	1

甘特图

在 P1 之后，P2 将被执行 4 个时间单位，如 GANTT 图表所示。

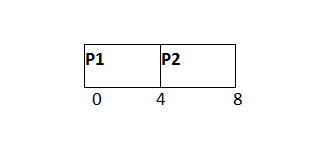
就绪队列

在执行P2期间，还有一个进程P6到达了就绪队列。由于P2尚未完成，因此P2将以剩余的执行时间2个单位重新添加到就绪队列中。

P3	P4	P5	P1	P6	P2
3	1	5	1	4	2

甘特图

在 P1 和 P2 之后，P3 将被执行 3 个时间单位，因为它的 CPU 增长时间仅为 3 秒。

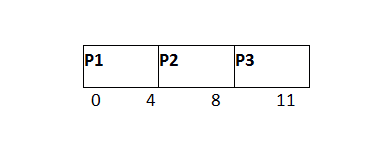
就绪队列

因为P3已经完成，因此它将被终止并不会被加入到就绪队列中。下一个将被执行的进程是P4。

P4	P5	P1	P6	P2
1	5	1	4	2

甘特图

在P1、P2和P3之后，P4将被执行。它的执行时间只有1个单位，小于时间片，因此将被完成。

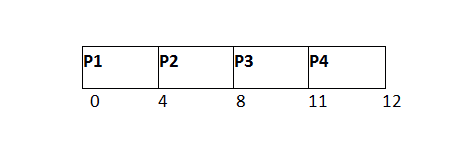
就绪队列

就绪队列中的下一个进程是具有5个单位的执行时间的P5。由于P4已经完成，所以它将不会再被加入队列。

P5	P1	P6	P2
5	1	4	2

甘特图

P5将被执行整个时间片，因为它需要5个单位的执行时间，高于时间片的长度。

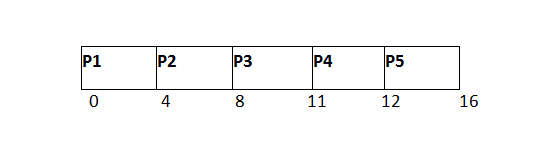
就绪队列

P5尚未完成；它将被添加回队列，并保留1个单位的剩余执行时间。

P1	P6	P2	P5
1	4	2	1

甘特图

进程P1将有机会完成其执行。由于它只需要1个单位的执行时间，因此它将被完成。

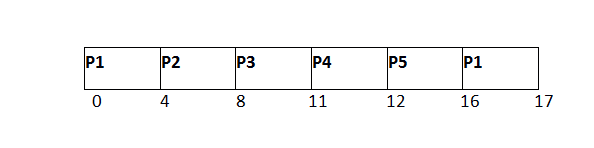
就绪队列

P1已经完成并且不会再被添加回就绪队列中。下一个进程P6只需要4个时间单位的执行时间，将会被下一步执行。

P6	P2	P5
4	2	1

甘特图

P6将在4个时间单位内执行完毕。

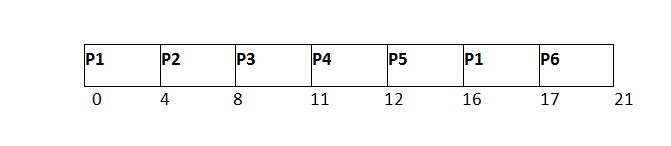
就绪队列

由于P6已经完成，因此不会再次添加到队列中。准备队列中只有两个进程。下一个进程P2只需要2个时间单位。

P2	P5
2	1

甘特图

因为只需要2个时间单位，所以P2会再次执行，因此P2将会被完成。

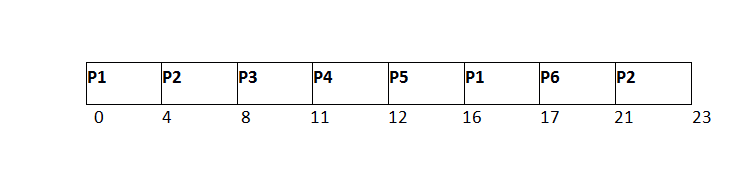
就绪队列

现在，队列中唯一可用的进程是P5，它需要1个单位的执行时间。由于时间片的长度为4个单位，因此它将在下一个执行时间片内完成。

P5
1

甘特图

P5将执行直到完成。

完成时间，周转时间和等待时间将根据下表所示进行计算。

如我们所知，

Turn Around Time = Completion Time - Arrival Time 
Waiting Time = Turn Around Time - Burst Time 

Process ID	Arrival Time	Burst Time	Completion Time	Turn Around Time	Waiting Time
1	0	5	17	17	12
2	1	6	23	22	16
3	2	3	11	9	6
4	3	1	12	9	8
5	4	5	24	20	15
6	6	4	21	15	11

平均等待时间 = (12+16+6+8+15+11)/6 = 76/6 单位