操作系统 轮换变量或严格轮换方法

轮换变量或严格轮换方法是在用户模式下实现的软件机制。这是一种忙等待的解决方案，只能用于两个进程。在这种方法中，使用一个被称为轮换变量的变量来实际上是一个锁。

这种方法只能用于两个进程。一般来说，让这两个进程分别为Pi和Pj。它们共享一个被称为轮换变量的变量。程序的伪代码可以如下所示。

对于进程Pi

Non - CS 
while (turn ! = i); 
Critical Section 
turn = j; 
Non - CS

对于进程 Pj

Non - CS 
while (turn ! = j);
Critical Section 
turn = i ;
Non - CS 

锁变量方法的实际问题在于，只有在锁变量为1时进程才能进入临界区。由于多个进程可以同时将锁变量视为1，因此无法保证互斥性。

这个问题在转向变量方法中得到解决。现在，进程只能在转向变量的值等于该进程的PID时才能进入临界区。

转向变量只有两个可能的值，i或j。如果它的值不是i，那么它肯定是j，反之亦然。

在进入区段中，一般情况下，进程Pi只有当其值为j时才能进入临界区，进程Pj只有当其值为i时才能进入临界区。

最初，两个进程Pi和Pj可用并且希望进入临界区。

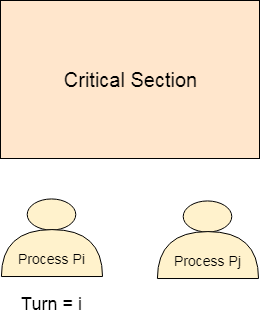
turn变量等于i，因此Pi将有机会进入临界区。直到Pi完成临界区，Pi的值保持为I。

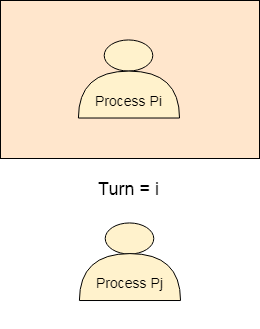
Pi完成其临界区，并将j分配给turn变量。 Pj将有机会进入临界区。在Pj完成其临界区之前，turn的值保持为j。

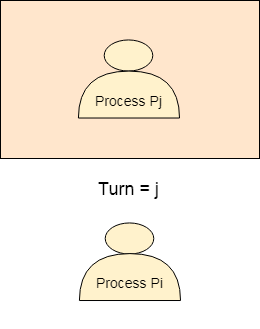
严格轮换方法的分析

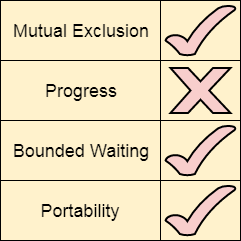
让我们根据四个要求来分析严格交替方法。

互斥性

严格交替方法在每种情况下都提供互斥性。该过程仅适用于两个进程。伪代码对于这两个进程是不同的。只有当进程看到转变变量等于其进程ID时，进程才能进入。因此，无论轮到哪个进程，都不能进入临界区。

进展性

在这种机制中，并不保证进展性。如果Pi不想在轮到它进入临界区时进入，那么Pj将被无限期地阻塞。Pj必须等待很长时间才能轮到它，因为在Pi将其分配给j之前，转变变量将保持为0。

可移植性

该解决方案提供了可移植性。它是在用户模式下实现的纯软件机制，不需要操作系统的任何特殊指令。