C++ 居中的八面体数

什么是居中的八面体数？让我们来解释一下。

首先，什么是八面体

八面体是一个八个面的、等边三角形形状的三维几何体。它有8个顶点，12条边和6个正方形面，是一个多面体。八面体是五种普朗克立体之一，它们是具有对称顶点排列和相同面的正多面体。

八面体有许多迷人的特点和用途，包括晶体学，用于描述某些晶体的结构，以及计算机图形学，用于建模三维物体。许多其他自然现象，包括一些病毒的结构和一些晶体的形状，也呈现出八面体的形状。

看一下下面的图示，你会清楚地了解八面体是什么。

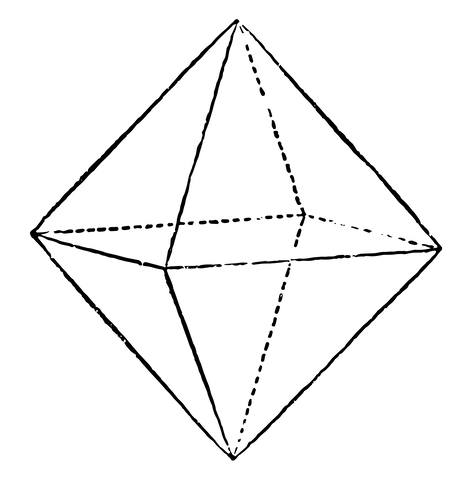
现在，什么是八面体数

八面体上等间距点的数量被八面体数所表示，它是一个象征性的数。换句话说，它是构建一个具有每层特定数量球的八面体所需的球的数量。

以下是最初的八面体数：

1, 6, 19, 44, 85, 146, 231, 344, 489, 670, …

八面体数的应用可以在许多领域找到，包括晶体学、化学和几何学。例如，它们用于指定可以组合在特定类型的化学结构中以包围一个核心原子的原子数量。

看一下下面的图示，以了解八面体数。

接下来是什么是居中的八面体数

由等间距点组成的八面体中心位于原点的点的数量被称为居中的八面体数。换句话说，它是在三维立方晶格中的原点处居中的八面体内的点阵点的数量。

以下是前几个居中的八面体数：

1, 7, 25, 63, 129, 231, 377, 575, 833, 1159, …

可以使用前n个居中的平方数的和的公式来得到第n个居中的八面体数的公式：

Sn = n(2n−1)(2n+1)/3

将前n个居中的平方数相加，然后乘以2，即可得到第n个居中的八面体数：

Co_n = 2Sn = 2n(2n−1)(2n+1)/3

简化这个表达式，我们得到：

Co_n = (2n+1)(2n^2+2n+3)/3

居中的八面体数用于指示在特定类型的化学结构中可以围绕中心原子分组的原子数。它们在许多领域，包括晶体学中很有用。它们也与二维格点路径计数Delannoy数有关。

方法

以下是计算居中的八面体数的逐步方法。

• 将n指定或作为用户输入

• 使用公式Co_n = (2n+1)(2n^2+2n+3)/3计算居中的八面体数

• 将居中的八面体数打印到控制台。

C++实现

太多理论？现在让我们看代码。让我们将上面讨论的方法转换为c++代码。

例子

#include <iostream>
using namespace std;

int centered_octahedral(int n) {
    return (2 * n + 1) * (2 * n * n + 2 * n + 3) / 3;
}

int main() {
    int n= 6;

    cout << "The " << n << "th centered octahedral number is: " << centered_octahedral(n) << endl;
    return 0;
}

输出

The 6th centered octahedral number is: 377

时间复杂度：O(1)

空间复杂度：O(1)

结论

在本文中，我们详细解释了中心八面体数以及计算第n个中心八面体数的方法。希望你现在对这个概念有了清晰的认识。