C++ 居中的三角形数

“居中的三角形数”这个术语你理解吗？让我们在本文中来解读一下。

首先，什么是三角形数？

对象或点的三角形排列可以用来代表一种被称为三角形数的图形数。前 n 个自然数的和就是第 n 个三角形数。

例如，前几个三角形数是：

1, 3, 6, 10, 15, 21

你可以将这些数字看作是由点组成的三角形集群，以演示它们是如何计算的，如下图所示：

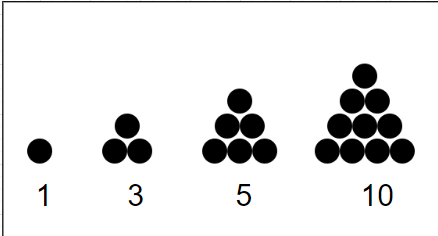
如果你仔细观察，你会发现：

1 = 1

3 = 1 + 2

6 = 1 + 2 + 3

10 = 1 + … + 4

15 = 1 + … + 5

21 = 1 + 2 + 3 + 4 + 5 + 6

因此，我们可以得出结论，找到第 n 个三角形数的公式是 n(n+1)/2。

现在，什么是居中的三角形数？

居中的三角形数是一种三角形数，它是通过在点的正三角形的中心放置一个单独的点来形成的。前几个居中的三角形数是：

1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166…

现在，看一下下面的图：

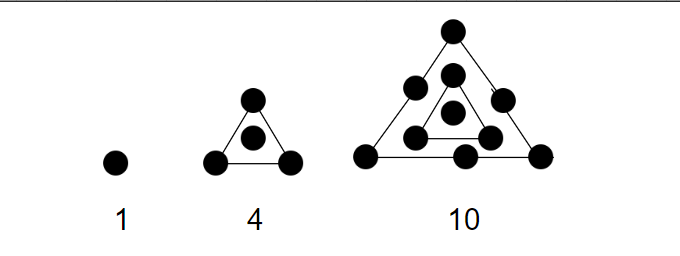
计算第 n 个居中三角形的公式是 C_n = 1 + 3(n(n+1)/2) = (3n^2+ 3n+2)/2

方法

现在，你知道了什么是居中的三角形数。我们来讨论一下编写相同功能的 C++ 代码的方法。

• 指定 n 的值，或者将其作为用户输入。

• 使用公式 (3n^2 + 3n + 2)/2 计算第 n 个居中三角形数。

• 将值打印到控制台。

C++实现

太多的理论了吗？让我们进入代码模式。下面是使用上述方法计算第 n 个居中三角形数的 C++ 代码实现。

示例

#include <iostream>
using namespace std;

int main() {
    int n= 10;

    int centered_triangular = (3*n*n + 3*n + 2)/2;
    cout << "The " << n << "th centered triangular number is: " << centered_triangular << endl;

    return 0;
}

输出

The 10th centered triangular number is: 166

时间复杂度：O（1）

空间复杂度：O（1）

结论

在这篇文章中，我们介绍了什么是三角数和什么是中心三角数。我们还探讨了计算第n个中心三角数的逻辑，并将其转化为C++代码。希望现在您对这个概念有一个清晰的理解，同时也希望您找到了这篇文章有用。