R语言 什么是DBScan聚类
聚类分析是机器学习和数据挖掘中的一种基本技术,可以用于识别模式并将相似的数据点分组在一起。在各种聚类算法中,基于密度的空间聚类应用与噪声(DBSCAN)算法以其能够自动发现任意形状的聚类而脱颖而出。在本文中,我们将探讨DBSCAN背后的概念,并通过清晰简洁的代码示例展示其在R编程中的实现。
DBScan聚类
DBSCAN在处理包含不同密度群组或不规则形状聚类的数据集时特别有价值。与其他传统聚类技术(如K-means或层次聚类)不同,DBSCAN基于密度可达点而不是预定义的距离阈值来确定聚类。
DBSCAN的关键参数
- Epsilon (ε): 作为同一聚类的两个相邻点之间的最大距离。
-
MinPts: 在ε距离内所需的最小邻居点数,用于将点分类为核心点。
-
边界点: 位于ε半径内但没有足够的邻居以被视为核心点的数据点。
-
噪声点: 远离任何聚类的离群值。
DBSCAN聚类的优势
-
处理噪声的能力: 与K-means或层次聚类等其他一些聚类算法不同,DBSCAN通过将噪声数据视为离群值或噪声而不是强制将它们分配到特定的聚类中,可以有效处理噪声数据。
-
灵活检测聚类形状: 传统方法往往假设球形或凸形聚类。然而,DBSCAN擅长识别具有复杂形状和不同密度的聚类,而无需先验假设。
-
自动确定聚类数量: 与K-means等方法不同,DBSCAN不需要事先了解所需聚类数量的先验知识-它可以自动发现最优的聚类数量。
-
对参数选择的鲁棒性: 尽管需要调整参数(epsilon和minPts),但它们具有直观的解释,与许多其他聚类算法相比,更容易调整。
-
适用于大规模数据集的可扩展性: 通过巧妙地利用k-d树或R树等索引结构以及高效的基于密度的计算,DBSCAN可以对高维数据或大规模数据集进行良好的扩展。
使用DBSCAN的劣势
-
参数敏感性: 选择合适的epsilon (ε)和minPts值是至关重要但具有挑战性的,因为这些参数很大程度上依赖于数据集的特征,如底层密度分布。选择不恰当的值可能导致合并聚类或创建过多的小而无关的聚类。
-
对密度变化的数据集效率低下: 传统的DBSCAN在数据集的密度在不同区域之间变化显著时会出现困难。虽然有改进的版本(如改进的DBSCAN)试图解决这个问题,但可能会增加计算复杂度的代价。
-
难以处理高维数据: 与许多聚类算法一样,DBSCAN在应用于高维数据集时面临挑战,原因是“维度灾难”。在这种情况下,可能需要在应用DBSCAN之前进行特征选择或降维技术。
使用R编程实现层次聚类
使用欧氏距离计算距离来实现DBSCAN聚类。下面的代码将在鸢尾花数据集上执行DBSCAN聚类,并使用带有突出显示的紫色聚类的散点图绘制结果聚类。
步骤
步骤1: 首先,我们需要安装和加载示例数据集。
步骤2: 在聚类之前,需要进行数据预处理。如果有缺失值,可能需要标准化变量或处理缺失值。
步骤3: 根据选择的度量(如欧氏距离或曼哈顿距离)计算观测值之间的不相似性或距离。
步骤4: 创建DBSCAN聚类,一旦我们准备好了距离矩阵,我们就可以使用R中的“hclust()”函数执行DBSCAN聚类。
步骤5: 生成的对象“hc”存储了后续步骤所需的所有信息。
步骤6: 绘制散点图,我们可以通过在R中绘制图来可视化我们的聚类。
示例
#install.packages("fpc")
# Load the fpc package
library(fpc)
# Load the iris dataset
data(iris)
# Standardize the iris dataset
iris_std <- scale(iris[-5])
# Calculate the distance matrix using Euclidean distance
distance_mat <- dist(iris_std, method = "euclidean")
# Create DBSCAN clusters
db_cl <- dbscan(distance_mat, eps = 0.5, MinPts = 5)
# Perform hierarchical clustering using Ward's method
hc <- hclust(distance_mat, method = "ward.D2")
# Plot the resulting dendrogram
plot(db_cl, iris_std, main="ed")
输出
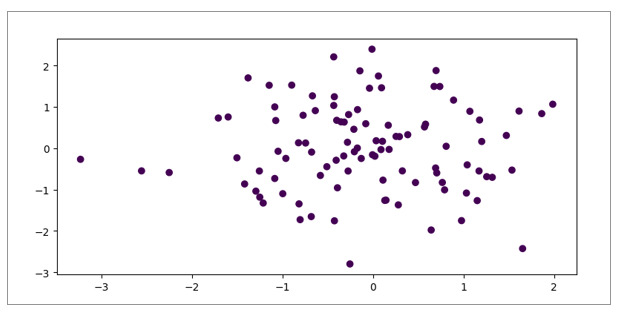
结论
DBSCAN在不依赖预定义距离或假设特定形状的聚类的情况下,为发现复杂数据集中隐藏模式提供了出色的替代方法。通过其自动识别噪声和异常值的能力,以及能够在单个分析中处理不同密度级别的灵活性,DBSCAN在各个领域均表现出极高的价值。
 极客笔记
极客笔记