操作系统 什么是Buddy系统

块的两个较小部分大小相等，被称为伙伴。Buddy系统是一种过程，其中两个独立的伙伴共同作为一个单一的单位运作，以便它们可以相互监视和帮助。同样，其中一个伙伴将进一步分割为更小的部分，直到请求被满足。

“梅里亚姆-韦伯斯特”是1942年Buddy系统这个短语的首次知名使用。根据韦伯斯特的定义，Buddy系统是一种安排，其中两个个体配对（如在危险情况下相互安全）。

Buddy系统基本上是在大组或单独的情况下成对工作。两个个体都必须完成工作。工作可以确保工作安全完成，或有效地从一个个体转移到另一个个体。

Buddy系统的类型

以下是四种Buddy系统的类型。

1. 二进制Buddy系统

Buddy系统维护每个大小的空闲块的列表（称为空闲列表），以便在需要时可以轻松找到所需大小的块。如果没有请求大小的块可用，Allocate会搜索第一个非空的块列表，以获取至少所需大小的块。在任何情况下，块都会从空闲列表中移除。

例如， 假设内存段的大小最初为256kb，并且内核请求25kb的内存。段最初被划分为两个伙伴，假设为A1和A2，每个大小为128kb。其中一个伙伴再被划分为两个大小为64kb的伙伴，假设为B1和B2。但是，最接近25kb的2的幂是32kb，因此，B1或B2将进一步分成两个大小为32kb的伙伴（C1和C2），最后使用其中一个伙伴来满足25kb的请求。拆分的块只能与其唯一的伙伴块合并，然后重新形成它们被拆分的较大块。

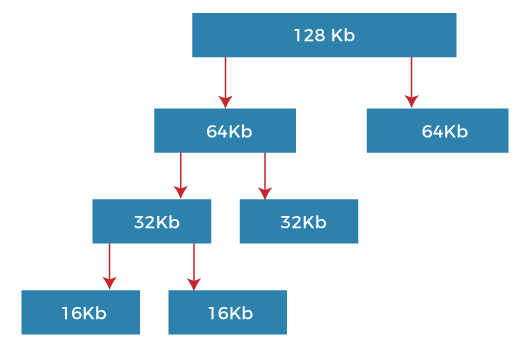
2. 斐波那契伙伴系统

斐波那契伙伴系统是一个将块划分为斐波那契数的大小的系统。它满足以下关系：

i (i-1) (i-2)

最初的斐波那契伙伴系统的过程要么限制在一个小、固定的块大小数量上，要么是一项耗时的计算。

3. 加权伙伴系统

加权伙伴系统与原始伙伴系统类似。在该系统中，大块被迭代地分割以提供所需的较小块。当块被释放时，如果存在伙伴，则将它们与其伙伴合并，否则将它们附加到可用空间列表中。二进制和加权伙伴系统具有以下相似之处。

• 容易计算块的伙伴的地址并给出块的地址。对于二进制和加权伙伴系统，地址计算是直观的。
• 从可用空间列表中分配块。

4. 三分伙伴系统

三分伙伴系统允许使用2k和3.2k大小的块，而原始的二进制伙伴系统只允许使用2k大小的块。这个扩展会额外消耗两个比特位。本文在C编程语言中实现了提出的算法的模拟。

对三分伙伴系统以及其他现有方案（例如二进制伙伴系统、斐波那契伙伴系统和加权伙伴系统）的内部碎片分析的性能分析在本研究中给出。此外，还讨论了对于上述系统的几种分割和平均合并次数的模拟结果的比较。

伙伴系统内存分配技术

伙伴系统内存分配技术是一种将内存分割为分区的算法，以尽可能地满足内存请求。该系统使用将内存分割成一半的方式来实现最佳匹配。伙伴内存分配相对容易实现。它支持有限但高效的内存块分割和合并。

伙伴内存分配算法

伙伴系统有多种形式，其中每个块被细分为两个较小的块是最简单和最常见的形式。在这个系统中，每个内存块都有一个 顺序 ，其中顺序是一个整数，范围从0到指定的 上限 。顺序为n的块的大小与 **2 n ** 成比例，因此块的大小是比低一个顺序的块恰好两倍。二的幂倍的块大小使得地址计算简单，因为所有伙伴均按照是2的次方数的内存地址边界对齐。

• 当一个较大的块被分割时，它会被分成两个较小的块，每个较小的块成为另一个块的唯一”buddy”（即成对块的名称）。一个分割块只能与它的唯一伙伴块合并，恢复为它们被分割的较大块。
• 确定最小可能的块大小，即可以分配的最小内存块。如果没有下限，系统将需要大量的内存和计算开销来跟踪内存中哪些部分是已分配的和未分配的。
• 但是一个较低的限制可能更好，以最小化每个分配的平均内存浪费（与不是最小块大小的倍数的分配有关）。
• 通常，下限应足够小以最小化每个分配的平均浪费空间，但足够大以避免过多的开销。最小块大小被作为0阶块的大小，以此来表示所有较高阶的大小都是这个大小的2的幂倍数。
• 然后程序员必须决定或编写代码以适应剩余的可用内存空间，以获得可能的最高阶。由于给定计算机系统的总可用内存可能不是最小块大小的2的幂倍数，最大的块大小可能无法覆盖整个系统内存。

例如，如果系统有2000 K的物理内存，且0阶块大小为4 K，则阶数的上限为8，因为8阶块（256个0阶块，1024 K）是适合该内存的最大块。因此，不可能将整个物理内存分配为单个块；剩余的976 K内存必须以较小的块分配。

优点

Buddy系统分配具有以下优点：

• 与其他简单技术相比，Buddy内存系统的外部碎片化较少。
• Buddy内存分配系统使用二叉树来表示已使用或未使用的分裂内存块。
• 分配正确大小的块。
• Buddy系统分配内存的速度非常快。
• 与最佳适应或首次适应算法相比，Buddy系统分配和释放内存的成本较低。
• 合并相邻空块很容易。
• 另一个主要优点是合并。这是指相邻的buddy是否能够快速合并为较大的段。这被称为合并。

缺点

它也有一些缺点，例如：

• 它要求所有分配单元都是2的幂。
• 它会导致内部碎片化。

Buddy系统内存分配示例

下面是一个程序请求内存时发生的情况示例。假设在该系统中，最小可能的块大小为64千字节，并且阶的上限为4，这将得到最大可分配的块为2 4 乘以64K = 1024K大小的结果。以下图像显示了各种内存请求后系统可能的状态。

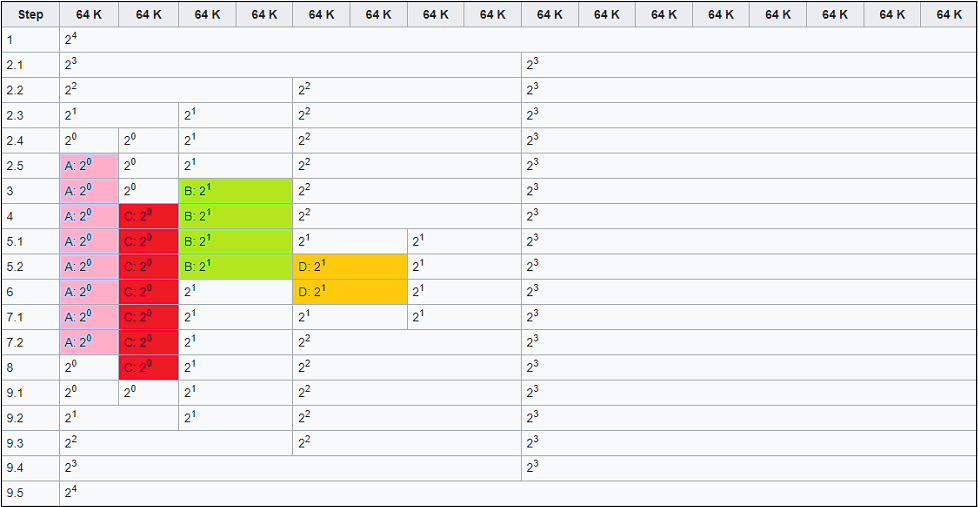
此内存分配可能按照以下方式进行。

步骤1： 这是初始情况。

步骤2： 程序A请求34K内存，级别0。

• 没有级别0块可用，因此分割一个级别4块，创建两个级别3块。
• 仍然没有级别0块可用，因此分割第一个级别3块，创建两个级别2块。
• 仍然没有级别0块可用，因此分割第一个级别2块，创建两个级别1块。
• 仍然没有级别0块可用，因此分割第一个级别1块，创建两个级别0块。
• 现在有一个级别0块可用，因此将其分配给A。

  步骤3： 程序B请求66K内存，级别1。有一个级别1块可用，因此将其分配给B。

  步骤4： 程序C请求35K内存，级别0。有一个级别0块可用，因此将其分配给C。

  步骤5： 程序D请求67K内存，级别1。

• 没有级别1块可用，因此分割一个级别2块，创建两个级别1块。

• 现在有一个级别1块可用，因此将其分配给D。

  步骤6： 程序B释放其内存，释放一个级别1块。

  步骤7： 程序D释放其内存。

• 一个级别1块被释放。

• 由于新释放块的伙伴块也是空闲的，所以它们合并成一个级别2块。

  步骤8： 程序A释放其内存，释放一个级别0块。

  步骤9： 程序C释放其内存。

• 一个级别0块被释放。

• 由于新释放块的伙伴块也是空闲的，所以它们合并成一个级别1块。
• 由于新形成的级别1块的伙伴块也是空闲的，所以它们合并成一个级别2块。
• 由于新形成的级别2块的伙伴块也是空闲的，所以它们合并成一个级别3块。
• 由于新形成的级别3块的伙伴块也是空闲的，所以它们合并成一个级别4块。

如上述步骤所示，当进行内存请求时，发生的情况如下：

1. 如果要分配内存。
   1. 寻找一个适合大小的内存槽（大于等于所请求内存的最小2的k次方块）。
   2. 如果找到，则将其分配给程序。
   3. 如果找不到，则尝试创建一个适合大小的内存槽。系统通过以下方式实现：
   • 将大于所请求内存大小的空闲内存槽分成两半。
   • 如果达到最小限制，则分配该内存量。
   • 返回并查找一个适合大小的内存槽（ 第I步 ）。
   • 重复此过程直到找到适合的内存槽。

2. 如果要释放内存。
   1. 释放内存块。
   2. 查看相邻的内存块。
   3. 如果相邻的内存块是空闲的，则将两个内存块合并，并返回到第II步，并重复此过程，直到达到上限（全部内存被释放）或遇到非空闲的相邻块为止。