机器学习 非线性SVM的应用
介绍
支持向量机(SVM)是最受欢迎的有监督机器学习算法之一,既用于分类又用于回归。SVM算法致力于找到最佳拟合线来将n维数据分为不同的类别。新的数据点可以被分类到这些类别之一。
SVM算法创建两个超平面,并最大化它们之间的间隔。位于这些超平面上的点被称为支持向量,因此被称为支持向量机。
下图显示了用于将数据划分为两个类别的SVM的决策边界和超平面。
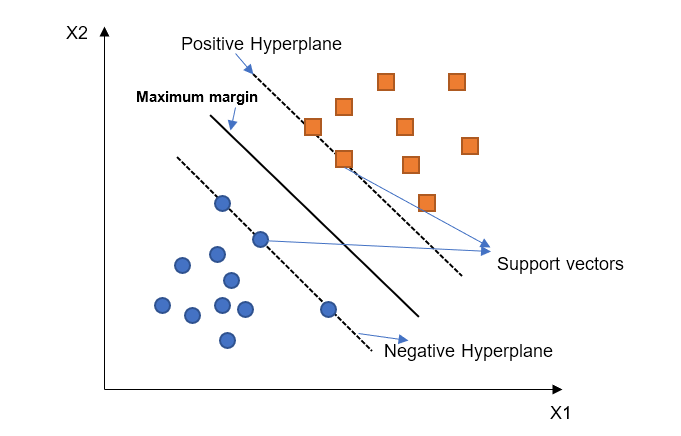
上图解释了线性SVM的工作原理。图中通过最大间隔超平面将两个类别相互分离。分离超平面旨在最大化负超平面和正超平面之间的间隔。支持向量分别是负超平面和正超平面上的点。
SVM算法的一个示例可以是一个分类器,用于将图像分类为猫和狗,给定一个包含猫和狗图像的数据集。
非线性SVM
我们在现实世界中收到的数据并不总是线性可分的。虽然线性SVM是线性数据的完美类型的SVM算法,但非线性数据可以通过使用非线性内核的非线性SVM来有效处理。
直线可以对两类进行分类,但对于多类分类,需要非线性SVM,因为数据可能是n维的。
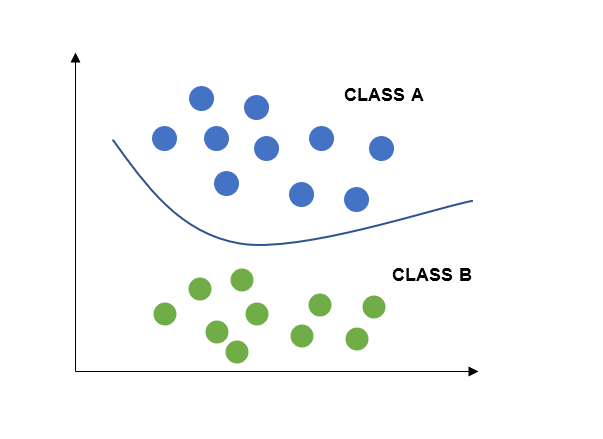
从上图可以看出,非线性SVM中分隔两个类别的超平面是非线性的。在上图中,类别A和类别B由非线性或曲线边缘或超平面分隔,该超平面倾向于最大化两个类别之间的间隔。
非线性SVM中最常用的内核是径向基函数(RBF)内核。然而,还有其他非线性内核,如多项式内核。
让我们了解更多关于RBF内核,并看看它如何在SVM中帮助进行非线性分类。
RBF内核
内核是一个将n维输入数据转换为m维的函数,使得n >> m。
RBF内核通过内核技巧将非线性可分数据变得几乎线性,并对数据进行转换。
RBF内核的表示如下。
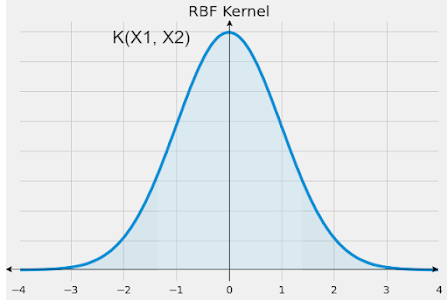
示例
import numpy as np
from sklearn import datasets as ds
from sklearn import svm
import matplotlib.pyplot as plt
%matplotlib inline
X, y = ds.make_circles(n_samples=500, noise=0.06)
plt.scatter(X[:, 0], X[:, 1], c=y, marker='.')
plt.show()
classifier_non_linear = svm.SVC(kernel='rbf', C=1.0)
classifier_non_linear.fit(X, y)
def boundary_plot(m, axis=None):
if axis is None:
axis = plt.gca()
limit_x = axis.get_xlim()
limit_x_y = axis.get_ylim()
x_lines = np.linspace(limit_x[0], limit_x[1], 30)
y_lines = np.linspace(limit_x_y[0], limit_x_y[1], 30)
Y, X = np.meshgrid(y_lines, x_lines)
xy = np.vstack([X.ravel(), Y.ravel()]).T
Plot = m.decision_function(xy).reshape(X.shape)
axis.contour(X, Y, Plot,
levels=[0], alpha=0.6,
linestyles=['-'])
plt.scatter(X[:, 0], X[:, 1], c=y, s=55)
boundary_plot(classifier_non_linear)
plt.scatter(classifier_non_linear.support_vectors_[:, 0], classifier_non_linear.support_vectors_[:, 1], s=55, lw=1, facecolors='none')
plt.show()
输出
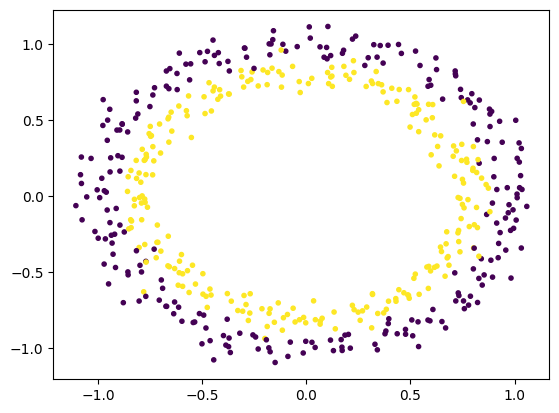
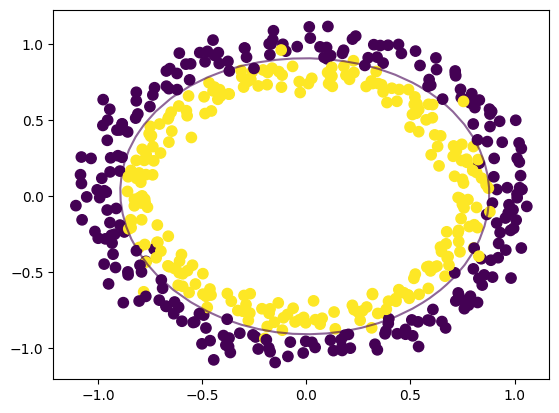
结论
非线性支持向量机是一种非常有用的工具和高效的算法,可以用于监督学习中的分类和回归。当数据不是线性可分时,它非常有用,可以利用非线性核函数(如RBF核函数和其他合适的函数)进行核技巧的应用。
 极客笔记
极客笔记