机器学习 为什么使用逻辑回归进行分类

介绍

逻辑回归是一种常用的二分类机器学习分类算法。尽管其名称中包含”回归”一词，但实际上它是一种分类算法。它使用对数几率和对数损失或交叉熵损失作为损失函数。

本文将介绍为什么逻辑回归是一种分类算法。

逻辑回归作为分类算法

线性回归算法可以用线性方程表示，一个包含\mathrm{\alpha_{0}}截距和\mathrm{\alpha_{1}}的单变量回归模型可以写成：

\mathrm{y=\alpha_{0}+\alpha_{1}x}

最佳拟合线如下图所示：

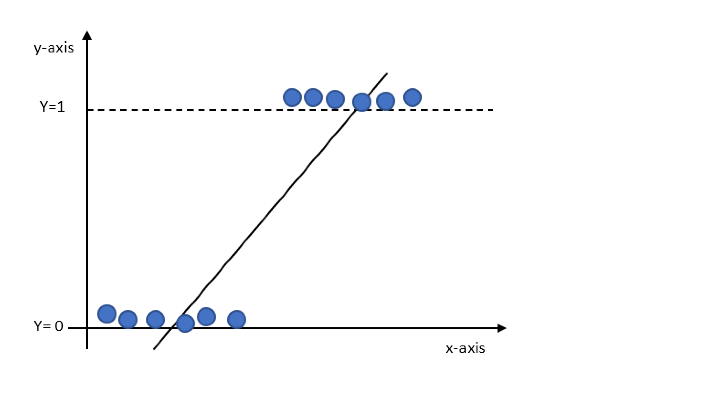
然而，在逻辑回归中，值只能在0和1之间，而在线性回归中，值是连续的，超出了0和1的范围。

这清楚地显示出线性回归方程必须转换，以适应范围为[0,1]的值。逻辑回归使用了一个sigmoid函数来实现这个目标，特别是在逻辑回归中，它将值压缩在0和1之间。

\mathrm{p(x)=\frac{1}{1+e^-({\alpha_{0}+\alpha_{1}}x)}}

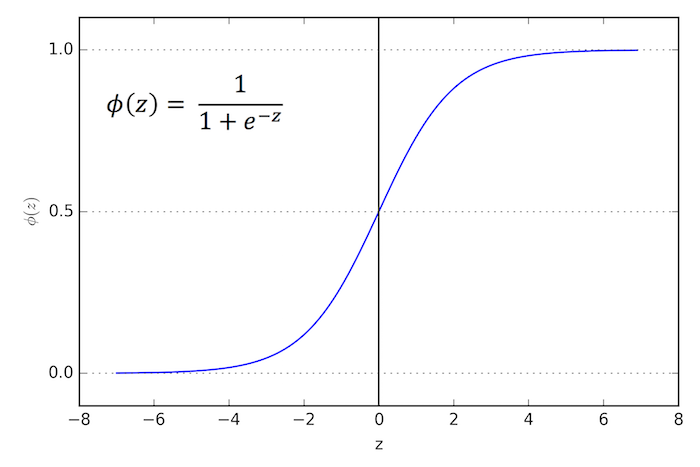
因此，我们可以用逻辑回归模型两个类别。

逻辑函数或sigmoid函数为\mathrm{\frac{1}{1+e^{−t}}}。

对数几率是逻辑函数的反函数。从线性回归的方程中，我们看到它可以输出负无穷到正无穷的实数值，并在0和1的边界内。但当我们用sigmoid函数转换线性回归方程后，转换函数的概率值开始落在0和1之间。这证明了逻辑回归是一种分类算法，不能用于回归。换句话说，逻辑回归根据边界或类别对线性回归的值进行分类。

多类别分类逻辑回归

使用逻辑回归，我们可以实现多类别分类。无论是二分类还是多分类，其核心思想是相同的，不过在多类别分类中，我们使用一对多（one-vs-all）分类的概念。根据以下方程，会有多个独立变量：

\mathrm{\log\frac{p}{1−p}=\alpha_{0}+\alpha_{1}x_{1}+\alpha_{2}x_{2}+\alpha_{3}x_{3}+……..+\alpha_{n}x_{n}}

在上述方程中，我们可以看到对数几率的值取决于n个独立变量。

结论

逻辑回归是一种分类算法，它输出0到1之间的概率值，而不是连续值。这是由于对线性回归方程应用的sigmoid函数转换。逻辑回归可用于二分类和多分类。