Matplotlib 画圆弧示意图|极客笔记

在Matplotlib画图时，有时需要构造一些示意图，方便观看数据，明白数据的意义。特别是在学校里做老师，或者研究生的论文配图。虽然很多图可以使用绘图软件，或者编辑软件来完成，但是修改起来就比较麻烦一些，如果使用matplotlib来生成，修改一些参数就可以重新生成新的图案，比使用绘图软件或编辑软件来得还快。特别是老师要求课堂上可以动态在修改参数的演示图，就更加来得方便了。下面就是假设老师要画的一个示意图，如图：

Matplotlib画圆弧示意图

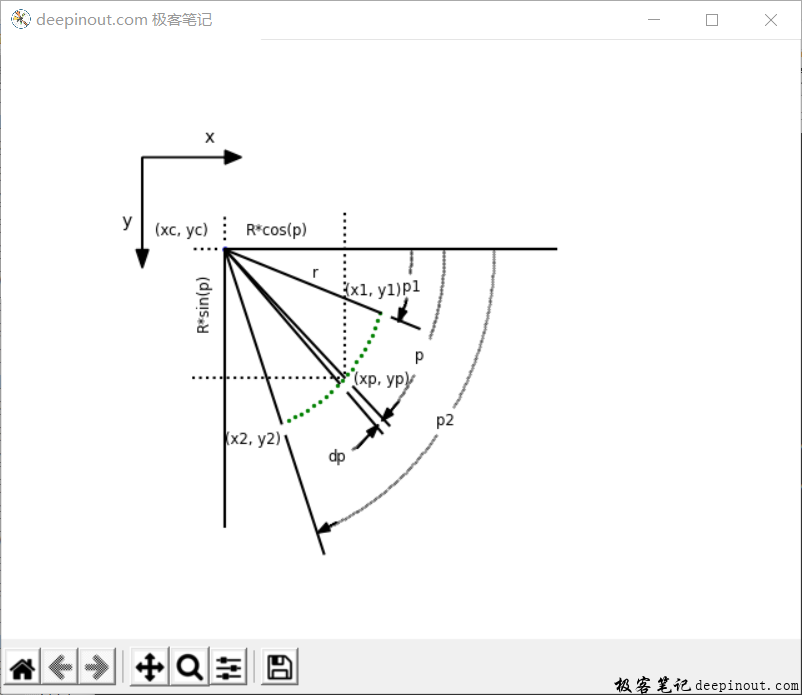
在这个图里，首先要使用前面学习过的知识来构造一个XY的辅助坐标系，有了这个辅助坐标系，就可以看到X轴和Y轴的方向，理解图像的数据大小的方向。其次，就要开始画一个圆心，然后再以圆心为中心点画一段圆弧，这段圆弧是以半径r为长度画的。接着连接圆心与端点（x1, y1）的直线，画p1示意线段，画p2示意线段。再接着连接圆心与点（x2, y2）的直线，然后画中间角度的变化量，再画dp指示线段。最后对整个图示进行标记，就完成了这个复杂示意图的构造。

当学生看到这个示意图，就可以知道角度，半径，变化量等内容，一目了然。虽然写起来代码来有点复杂，但是可以复用，因为可以适应不同的半径变化，以及不同的角度的修改，并且再次修改起来非常快捷。

因此一个老师掌握这种知识，就会很有用，可以把课件做到生动，并且可以随时修改。另外学生把这个学会之后，就可以用来画出很好的示意图，当作论文的插图。

整个程序里使用了画圆的参数方程：

X = XC + R*COS(phi)

Y = YC + R*SIN(phi)

联合matplotlib里的函数：

plt.arrow、plt.text、plt.scatter、plt.plot。

整个程序的源码有点长，可以一段一段地拷贝上去运行，这样就可以理解每段代码是干什么用的了，这样不用一下子就去学习整个代码，各个击破。

import numpy as np
import matplotlib.pyplot as plt

plt.figure('deepinout.com 极客笔记')
plt.axis([-10, 140, 90, -10])

plt.axis('off')
plt.grid(False)

#显示辅助坐标系
plt.arrow(0,0, 20,0, head_length = 4, head_width = 3, color = 'k')
plt.arrow(0,0, 0,20, head_length = 4, head_width = 3, color = 'k')
plt.text(15, -3, 'x')
plt.text(-5, 15, 'y')

#
xc = 20
yc = 20
r = 40
#画圆心
plt.scatter(xc, yc, color = 'b', s = 5)
#画一段圆弧
phi1 = 20*np.pi/180.0
phi2 = 70*np.pi/180.0
dphi = (phi2 - phi1)/20.0
for phi in np.arange(phi1, phi2, dphi):
    x = xc + r*np.cos(phi)
    y = xc + r*np.sin(phi)
    plt.scatter(x, y, s = 2, color = 'g')

#连接圆心与端点（x1,y1)
plt.plot([xc, xc + r*np.cos(phi1)], [yc, yc + r*np.sin(phi1)], color = 'k')

#p1指示线段
x1 = xc + (r + 3)*np.cos(phi1)
x2 = xc + (r + 10)*np.cos(phi1)
y1 = yc + (r + 3)*np.sin(phi1)
y2 = yc + (r + 10)*np.sin(phi1)
plt.plot([x1, x2], [y1, y2], color = 'k')

#p2指示线段
x1 = xc + (r + 3)*np.cos(phi2)
x2 = xc + (r + 30)*np.cos(phi2)
y1 = yc + (r + 3)*np.sin(phi2)
y2 = yc + (r + 30)*np.sin(phi2)
plt.plot([x1, x2], [y1, y2], color = 'k')

#连接圆心与端点（x2, y2)
plt.plot([xc, xc + r*np.cos(phi2)], [yc, yc + r*np.sin(phi2)], color = 'k')

#中间位置显示角度变化量
phihalf = (phi1 + phi2)*0.5
phi3 = phihalf - dphi/2
phi4 = phihalf + dphi/2

plt.plot([xc, xc + r*np.cos(phi3)], [yc, yc + r*np.sin(phi3)], color = 'k')
plt.plot([xc, xc + r*np.cos(phi4)], [yc, yc + r*np.sin(phi4)], color = 'k')

#dp1指示线段
x1 = xc + (r + 3)*np.cos(phi3)
x2 = xc + (r + 15)*np.cos(phi3)
y1 = yc + (r + 3)*np.sin(phi3)
y2 = yc + (r + 15)*np.sin(phi3)
plt.plot([x1, x2], [y1, y2], color = 'k')

#dp2指示线段
x1 = xc + (r + 3)*np.cos(phi4)
x2 = xc + (r + 15)*np.cos(phi4)
y1 = yc + (r + 3)*np.sin(phi4)
y2 = yc + (r + 15)*np.sin(phi4)
plt.plot([x1, x2], [y1, y2], color = 'k')

#p1圆弧
dphi = (phi3)/100
for phi in np.arange(0, phi1/2 - 3.2*np.pi/180, dphi):
    x = xc + (r + 5)*np.cos(phi)
    y = yc + (r + 5)*np.sin(phi)
    plt.scatter(x, y, s = 0.1, color = 'k')

for phi in np.arange(phi1/2 + 3.3*np.pi/180, phi1, dphi):
    x = xc + (r + 5)*np.cos(phi)
    y = yc + (r + 5)*np.sin(phi)
    plt.scatter(x, y, s = 0.1, color = 'k')

#p2圆弧
dphi = (phi3)/100
for phi in np.arange(0, phi2/2 - 3.2*np.pi/180, dphi):
    x = xc + (r + 25)*np.cos(phi)
    y = yc + (r + 25)*np.sin(phi)
    plt.scatter(x, y, s = 0.1, color = 'k')

for phi in np.arange(phi2/2 + 3.2*np.pi/180, phi2, dphi):
    x = xc + (r + 25)*np.cos(phi)
    y = yc + (r + 25)*np.sin(phi)
    plt.scatter(x, y, s = 0.1, color = 'k')
#p圆弧
dphi = (phi3)/100
for phi in np.arange(0, phi3/2 - 0.5*np.pi/180, dphi):
    x = xc + (r + 13)*np.cos(phi)
    y = yc + (r + 13)*np.sin(phi)
    plt.scatter(x, y, s = 0.1, color = 'k')

for phi in np.arange(phi3/2 + 9.0*np.pi/180, phi3, dphi):
    x = xc + (r + 13)*np.cos(phi)
    y = yc + (r + 13)*np.sin(phi)
    plt.scatter(x, y, s = 0.1, color = 'k')
#dp圆弧
dphi = (phi3)/100
for phi in np.arange(phi3 + 5*dphi, phi3 + 25*dphi, dphi):
    x = xc + (r + 13)*np.cos(phi)
    y = yc + (r + 13)*np.sin(phi)
    plt.scatter(x, y, s = 0.1, color = 'k')
#画直角坐标线
plt.plot([xc, 100], [yc, yc], 'k')
plt.plot([xc, xc], [yc, 80], 'k')

#显示标签
plt.text(71, 58, 'p2', size = 'small')
plt.text(66, 44, 'p', size = 'small')
plt.text(63, 29, 'p1', size = 'small')
plt.text(45, 66, 'dp', size = 'small')
plt.text(41, 26, 'r', size = 'small')
plt.text(3, 17, '(xc, yc)', size = 'small')

#显示R*COS
plt.plot([xc + r*np.cos(phi3), xc + r*np.cos(phi3)], [yc - 8, yc + r*np.sin(phi3)], 'k:')
plt.plot([xc, xc], [yc-2, yc - 8], 'k:')

plt.text(25, 17, 'R*cos(p)', size = 'small')

#显示R*SIN
plt.plot([xc - 8, xc + r*np.cos(phi3)], [yc + r*np.sin(phi3), yc + r*np.sin(phi3)], 'k:')
plt.plot([xc - 2, xc - 8], [yc, yc], 'k:')
plt.text(13, 37, 'R*sin(p)', size = 'small', rotation = 90)

#
plt.text(49, 30, '(x1, y1)', size = 'small')
plt.text(20, 62, '(x2, y2)', size = 'small')
plt.text(51, 49, '(xp, yp)', size = 'small')

#显示箭头
#p2
plt.arrow(47, 79, -2, 1, head_length = 3, head_width = 2, color = 'k')
#p
plt.arrow(62, 53, -2, 2, head_length = 3, head_width = 2, color = 'k')
#p1
plt.arrow(64, 31, -0.9, 2, head_length = 3, head_width = 2, color = 'k')
#dp
plt.arrow(52, 63, 3, -3, head_length = 3, head_width = 2, color = 'k')

plt.show()