Matplotlib 画圆弧示意图学习了圆的示意图,如果让你再做出一个椭圆的示意图呢,你也许以为很简单的,其实不是这样的。因为椭圆的方程需要改写才可以使用到程序里,否则画出来的图,与直线相交的图不在同一个坐标点上。这是由于实际画图的坐标轴不是按比例显示所致,要适应这种情况,就需要使用角度来计算椭圆坐标的点,这样无论比例怎么变化,但是角度不会变形。
椭圆上坐标点公式:
xp = r*cos(p) yp = r*sin(p)可以得到tan(p)= yp/xp,得到:
yp = xp*tan(p)
把上式代码椭圆方程:
x^2/a^2 + y^2/b^2 = 1
就可以计算出来:
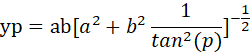
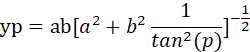
通过上面的公式,就可以确认椭圆的坐标了。假如老师要画下面的示意图:
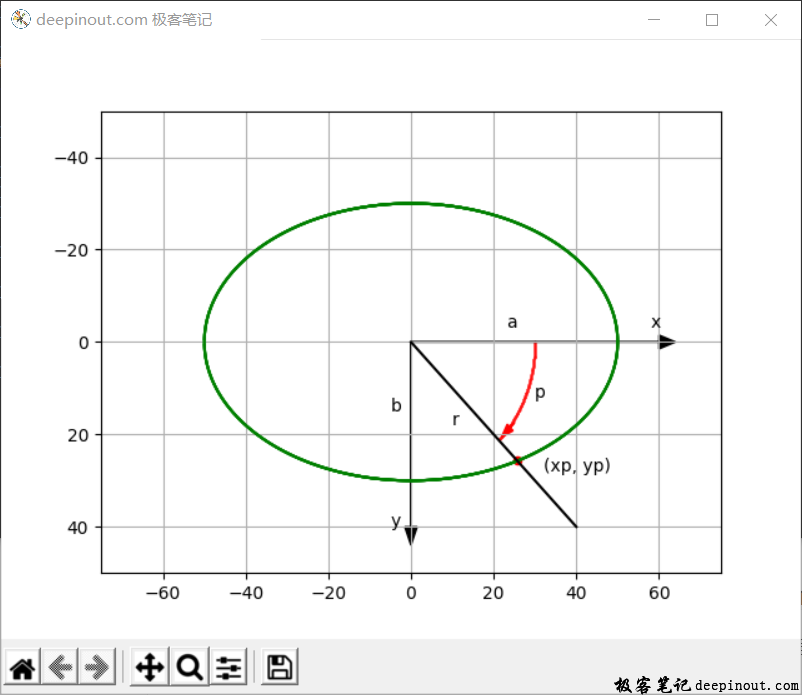
在这个示意图里,首先画了一个绿色的椭圆,然后画上指示坐标系,再画出45度角时的交点(xp, yp),最后画出角度p的标记线,还把椭圆与半径轴r的交点标记出来。通过这个示意图就可以让学生明白椭圆变化的关系。
要作出这样的示意图,需要使用matplotlib的编程,并且可以随时修改,并且随着不同的缩放也不会变形,因为这是代码实时生成,不像绘图软件或者办公软件画出来的,这样的示意图可以生成不同大小试卷的示意图,并且不会因为放大或缩小而失真。
整个演示的代码如下:
import numpy as np
import matplotlib.pyplot as plt
plt.figure('deepinout.com 极客笔记')
plt.axis([-75, 75, 50, -50])
plt.axis('on')
plt.grid(True)
#显示辅助坐标系
plt.arrow(0,0, 60,0, head_length = 4, head_width = 3, color = 'k')
plt.arrow(0,0, 0,40, head_length = 4, head_width = 3, color = 'k')
plt.text(58, -3, 'x')
plt.text(-5, 40, 'y')
#画的椭圆
a = 50.0
b = 30.0
p1 = 0.000001
p2 = 180.0*np.pi/180.0
dp = 0.2*np.pi/180.0
xlast = a
ylast = 0
for p in np.arange(p1, p2, dp):
xp = np.abs(a*b*(b*b+a*a*(np.tan(p))**2.0)**-0.5)
yp = np.abs(a*b*(a*a+b*b/(np.tan(p)**2.0))**-.5)
if p > np.pi/2:
xp = -xp
plt.plot([xlast, xp], [ylast, yp], color = 'g')
plt.plot([xlast, xp], [-ylast, -yp], color = 'g')
xlast = xp
ylast = yp
#画45度交点直线和交点标记
plt.plot([0, 40], [0, 40], color = 'k')
p = 45.0*np.pi/180.0
xp = np.abs(a*b*(b*b+a*a*(np.tan(p))**2.0)**-0.5)
yp = np.abs(a*b*(a*a+b*b/(np.tan(p)**2.+0.0001))**-.5)
plt.scatter(xp, yp, s = 20, color = 'r')
#标记文本
plt.text(23, -3, 'a', color = 'k')
plt.text(-5, 15, 'b', color = 'k')
plt.text(32, 28, '(xp, yp)')
plt.text(30, 12, 'p')
plt.text(10, 18, 'r')
#45度弧度标记
p1 = 0
p2 = 45*np.pi/180
dp = (p2 - p1)/180
r = 30
for p in np.arange(p1, p2, dp):
x = r*np.cos(p)
y = r*np.sin(p)
plt.scatter(x, y, s = 0.1, color = 'r')
plt.arrow(25, 17.5, -1, 1, head_length = 3, head_width = 2, color = 'r')
plt.show()主要使用到的函数有:
plt.axis、plt.grid、plt.arrow、plt.text、plt.plot、plt.scatter。
通过角度来计算椭圆的坐标,然后通过直线连接起来所有的点,就可以生成椭圆曲线。
 极客笔记
极客笔记