Matplotlib 画旋转向量示意图|极客笔记

作为一个数学老师，当你需要讲向量时，需要使用一些示意图，或者需要动态地修改一下向量的旋转关系。如果作为一个物理老师，也需要讲述力向量的方向和合成。如果需要现场可以动态在修改示意图时，你再采用预先绘制的方式，就不会适用，这时就可以采用matplotlib来动态编程，以便课堂上动态在修改，也可以分发给学生去研究和探索更多的可能性。如果只是给一个PPT，只能看看，而不能动手，也不能更进一步研究这些问题。这样对于学生来说，印象不会很深刻，也不会培训学生动手能力。

下面就来介绍一下，怎么样构造下面的旋转示意图：

Matplotlib画旋转向量示意图

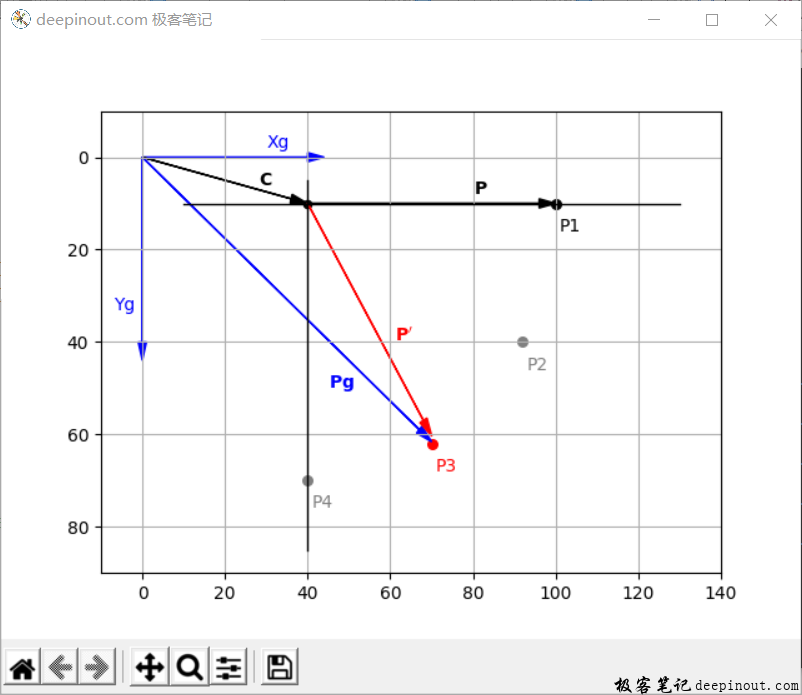
要画出这个示意图，首先要学会前面学习的辅助坐标系的表示，这样就可以表示原点所在位置，以及坐标轴的方向Xg，Yg。接着下来确定一个旋转中心C点，以C点为起点指向P1点的向量P，然后把向量P向点P2、P3、P4旋转，这里要注意的是绕着C点旋转，而不是原点。

在这里关键点就是旋转的实现，而二维图形的旋转是一个二维矩阵的变换，它是一个线性变换，公式如下：

Matplotlib画旋转向量示意图

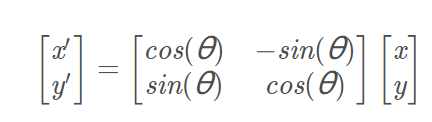
因此在代码实现这个函数：

#定义旋转矩阵

def rotz(xp, yp, rz):

    c11 = np.cos(rz)

    c12 = -np.sin(rz)

    c21 = np.sin(rz)

    c22 = np.cos(rz)

    xpp = xp * c11 + yp * c12

    ypp = xp * c21 + yp * c22

    xg = xc + xpp

    yg = yc + ypp

    return [xg, yg]

在这个函数先计算四个旋转量的矩阵，然后再计算出矩阵乘法之后的值，就是旋转后的位置。如果搞懂了这个，其它代码就是一些功能代码，比如画向量的箭头线段，标记点的位置，就可以显示整个示意图了。

整个例子的代码如下：

import numpy as np
import matplotlib.pyplot as plt

plt.figure('deepinout.com 极客笔记')
plt.axis([-10, 140, 90, -10])

plt.axis('on')
plt.grid(True)

#显示辅助坐标系
plt.arrow(0,0, 40,0, head_length = 4, head_width = 2, color = 'b')
plt.arrow(0,0, 0,40, head_length = 4, head_width = 2, color = 'b')
plt.text(30, -2, 'Xg', color = 'b')
plt.text(-7, 33, 'Yg', color = 'b')

#
xc = 40
yc = 10

plt.plot([xc - 30, xc + 90], [yc, yc], linewidth = 1, color = 'k') #X轴
plt.plot([xc, xc], [yc - 5, yc + 75], linewidth = 1, color = 'k') #Y轴
plt.scatter(xc, yc, s = 20, color = 'k')

#定义旋转矩阵
def rotz(xp, yp, rz):
    c11 = np.cos(rz)
    c12 = -np.sin(rz)
    c21 = np.sin(rz)
    c22 = np.cos(rz)

    xpp = xp * c11 + yp * c12
    ypp = xp * c21 + yp * c22
    xg = xc + xpp
    yg = yc + ypp

    return [xg, yg]

#
xp = 60
yp = 0

#P1
rz = 0
rz = rz * np.pi/180
[xg, yg] = rotz(xp, yp, rz)
plt.scatter(xg, yg, s = 30, color = 'k')
plt.text(xg + 1, yg + 6, 'P1', color = 'k')

#P2
rz = 30
rz = rz * np.pi/180
[xg, yg] = rotz(xp, yp, rz)
plt.scatter(xg, yg, s = 30, color = 'grey')
plt.text(xg + 1, yg + 6, 'P2', color = 'grey')

#P3
rz = 60
rz = rz * np.pi/180
[xg, yg] = rotz(xp, yp, rz)
plt.scatter(xg, yg, s = 30, color = 'r')
plt.text(xg + 1, yg + 6, 'P3', color = 'r')

xpp3 = xg
ypp3 = yg

#P4
rz = 90
rz = rz * np.pi/180
[xg, yg] = rotz(xp, yp, rz)
plt.scatter(xg, yg, s = 30, color = 'grey')
plt.text(xg + 1, yg + 6, 'P4', color = 'grey')

#向量标记
plt.arrow(0, 0, xc - 4, yc - 1, head_length = 4, head_width = 2, color = 'k')
plt.text(28, 6, r' $\mathbf{C}$ ', color = 'k')

plt.arrow(0, 0, xpp3 - 3, ypp3 - 3, head_length = 4, head_width = 2, color = 'b')
plt.text(45, 50, r' $\mathbf{Pg}$ ', color = 'b')

plt.arrow(xc, yc, xpp3 - 2 - xc, ypp3 - 5 - yc, head_length = 4, head_width = 2, color = 'r')
plt.text(61, 40, r' $\mathbf{P^{\prime}}$ ', color = 'r')

plt.arrow(xc, yc, xp - 4, yp, head_length = 4, head_width = 2, color = 'k')
plt.text(80, yc - 2, r' $\mathbf{P}$ ', color = 'k')

plt.show()

在例子里，主要四个点分别旋转30度、60度、90度的情况。