Matplotlib 一元线性回归显示|极客笔记

Matplotlib 四个Y轴显示学习了多个Y轴的显示，接着下来对多个Y轴的例子进行一些应用，比如实现一元线性回归的数据显示。因为一元线性回归在实验中经常地使用到，比如质量和重量的实验，比如计算热功当量。另外，由于实验做的次数总是有限的，要想把实验的数据进行推广应用，往往要把数据抽象成一个模型，那么就需要把数据进行回归分析，去掉实验中误差比较大的点。

回归分析只涉及到两个变量的，称一元回归分析。一元回归的主要任务是从两个相关变量中的一个变量去估计另一个变量，被估计的变量，称因变量，可设为Y；估计出的变量，称自变量，设为X。回归分析就是要找出一个数学模型Y=f(X)，使得从X估计Y可以用一个函数式去计算。当Y=f(X)的形式是一个直线方程时，称为一元线性回归。这个方程一般可表示为Y=A+BX。根据最小平方法或其他方法，可以从样本数据确定常数项A与回归系数B的值。A、B确定后，有一个X的观测值，就可得到一个Y的估计值。回归方程是否可靠，估计的误差有多大，都还应经过显著性检验和误差计算。有无显著的相关关系以及样本的大小等等，是影响回归方程可靠性的因素。

由于在学习和工作中，经常会使用到，因此学会一元线性回归是必要的技巧。下面就演示采用matplotlib来实现一元线性回归的计算和显示。如下图：

Matplotlib一元线性回归显示

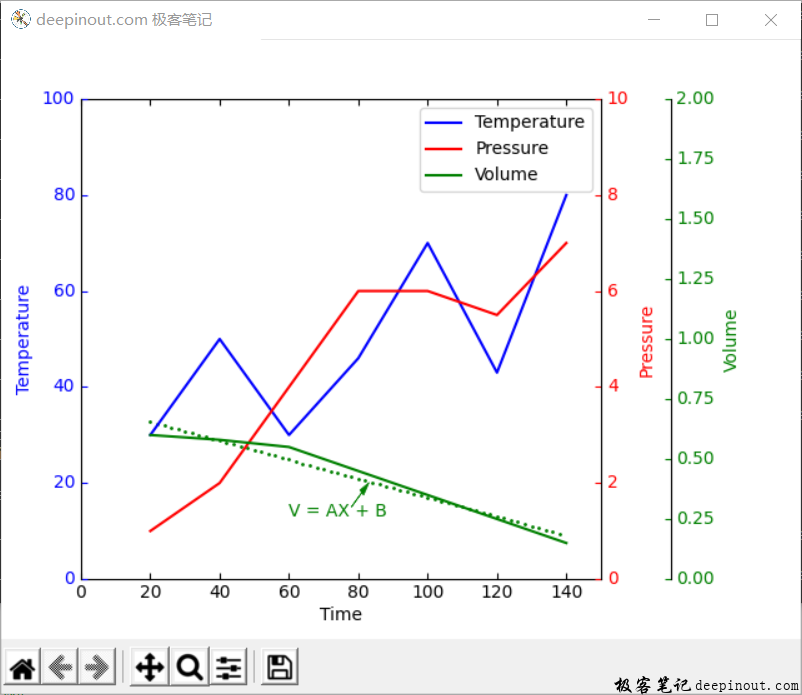
上图中，针对前面的数据V进行线性回归拟合，然后在图里显示一条点线，并作出V = AX +B的标记。

在程序里，主要采用下面的公式来计算一元线回归：

Matplotlib一元线性回归显示

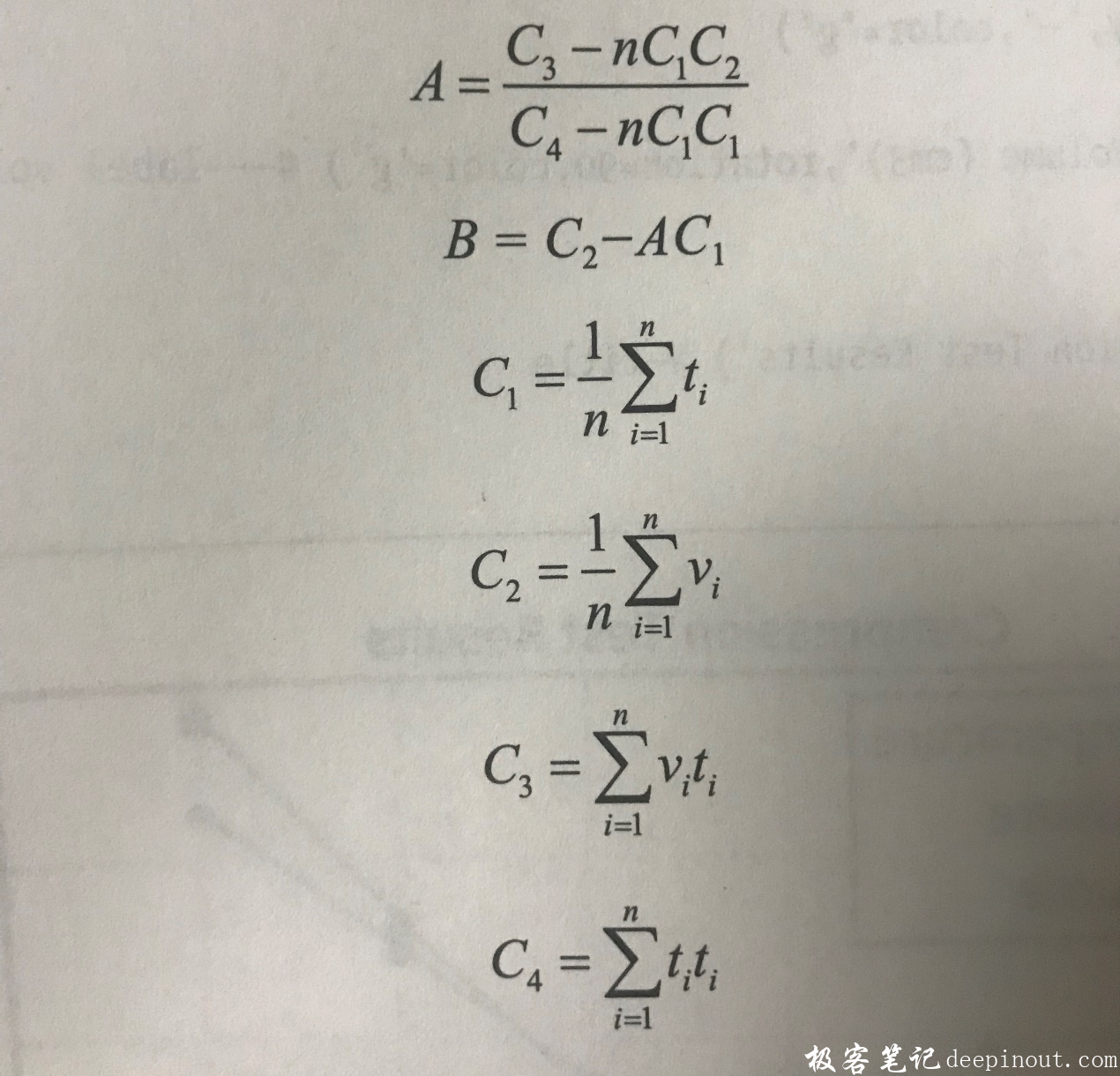
由公式可见，只要计算4个C1，C2, C3, C4的系数，就可以计算出来A和B的系数，从而画出平Y=AX + B的直线。

整个例子的代码如下：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axisartist.parasite_axes import HostAxes, ParasiteAxes


#定义显示的数据
x = [20, 40, 60, 80, 100, 120, 140]
T = [30, 50, 30, 46, 70, 43, 80]
P = [1.0, 2.0, 4.0, 6.0, 6.0, 5.5, 7.0]
V = [0.6, 0.58, 0.55, 0.45, 0.35, 0.25, 0.15]

#
fig = plt.figure('deepinout.com 极客笔记')

host = HostAxes(fig, [0.10, 0.1, 0.65, 0.8])
par1 = ParasiteAxes(host, sharex=host)
par2 = ParasiteAxes(host, sharex=host)


host.parasites.append(par1)
host.parasites.append(par2)
host.axis["right"].set_visible(False)

par1.axis["right"].set_visible(True)
par1.axis["right"].major_ticklabels.set_visible(True)
par1.axis["right"].label.set_visible(True)

#设置每条轴的名称
host.set_xlabel("Time")
host.set_ylabel("Temperature")
par1.set_ylabel("Pressure")
par2.set_ylabel("Volume")

# 于 offset 处新建一条纵坐标
offset = (40, 0)
new_axisline = par2.get_grid_helper().new_fixed_axis
par2.axis["right2"] = new_axisline(loc="right", axes=par2, offset=offset)


fig.add_axes(host)

#画三条曲线
p1, = host.plot(x, T, "b-", label="Temperature")
p2, = par1.plot(x, P, "r-", label="Pressure")
p3, = par2.plot(x, V, "g-", label="Volume")

#进行线性回归计算和显示
n = len(V)

c1 = np.sum(x)/n
c2 = np.sum(V)/n
a = np.multiply(V, x)
c3 = np.sum(a)
a = np.multiply(x, x)
c4 = np.sum(a)

A = (c3 - n*c1*c2)/(c4 - n*c1*c1)
B = c2 - A*c1
#显示线性回归的曲线
for tp in np.arange(x[0], x[6], 2): 
    vp = A*tp + B
    par2.scatter(tp, vp, color = 'g', s = 1)
#误差计算
sumee = 0
for i in range(len(x)):
    e = (V[i] - (A*x[i] + B))
    ee = e * e
    sumee = sumee + ee
    rms = np.sqrt(sumee/n)

#进行标记
plt.text(60, 13, 'V = AX + B', color = 'g')
plt.arrow(78, 15, 3, 3, head_length = 3, head_width = 1.5, color = 'g', linewidth = 0.5)

#设置X和三条Y轴的刻度范围
host.set_xlim(0, 150)
host.set_ylim(0, 100)
par1.set_ylim(0, 10)
par2.set_ylim(0, 2)

#设置轴名称的颜色
host.axis["left"].label.set_color(p1.get_color())
par1.axis["right"].label.set_color(p2.get_color())
par2.axis["right2"].label.set_color(p3.get_color())

#设置轴刻度线的颜色
host.axis["left"].major_ticks.set_color(p1.get_color())
par1.axis["right"].major_ticks.set_color(p2.get_color())
par2.axis["right2"].major_ticks.set_color(p3.get_color())

host.axis["left"].major_ticklabels.set_color(p1.get_color())
par1.axis["right"].major_ticklabels.set_color(p2.get_color())
par2.axis["right2"].major_ticklabels.set_color(p3.get_color())


#生成图例
lines = [p1, p2, p3]
host.legend(lines, [l.get_label() for l in lines])

plt.show()