C++ DES数据加密标准算法
简介
信息时代的来临产生了大量的数据。由于保护敏感信息对于维护人们的隐私变得越来越重要,因此在网络传输和系统内存中存储信息的方式受到了更多的重视。
DES(数据加密标准)算法由IBM开发。它是一种基于Horst Feistel在20世纪70年代的科学计算技术创造的旧算法的对称密钥技术。对称密钥算法使用相同的密钥来加密和解密消息和密码文。该算法得到了美国国家标准局的算法认可。
在与美国国家安全局(NSA)进行讨论后,DES算法在1976年进行了一些调整。随后,该算法在1977年在美国被正式发布为联邦信息处理标准(FIPS)。
描述DES算法
数据加密标准算法是一种分组密码方法,它使用48位密钥对每个输入进行加密,并将64位明文块转换为64位的密码块。需要加密的文本被分成称为块的单元,每个块都会使用块密码技术中的密钥进行单独加密。
解密步骤完全颠倒了加密过程。在加密过程中使用相同的48位密钥,它接受64位的密文块并输出64位的明文块。为了使加密者和解密者能够相互交互,必须使用相同的密钥。
DES算法在互联网的早期取得了成功,但由于其不足的56位密钥长度,当今的应用程序无法使用它。随着技术的进步和处理能力的提高,一个坚决的攻击者可以很快地通过正确的工具破解密钥。然而,它对密码学的发展和发展产生了重大影响。
如何创建密钥
计算机不使用字母和数字。在加密之前,所有明文字符都被转换为二进制。在整个加密过程中,数据被分成块进行处理。DES算法将二进制明文分成64位的块,从而得到64位的块大小。
在执行任何其他操作之前,如果最后一个块的长度不完全是64位,则对其进行填充。填充确保在块中包括其他数据以增加其长度至64位。填充可以确保加密数据更难解密。 为了防止攻击者仅仅通过了解算法来预测明文,使用密钥来改变加密操作的结果。 在DES中,使用单个密钥来创建后续每个”轮”所使用的密钥。DES算法被应用了16次才生成最终的密文;每次应用都被称为一轮,其结果作为下一轮的输入。它可以最大程度地增加明文的混淆度。 现在,我们首先选择一个随机的64位值作为我们的密钥K。记住,为了进行通信,发送方和接收方必须拥有相同的64位密钥。 每一轮必须有一个子密钥。这个子密钥是独特于该轮的,并且是我们在开始时建立的主密钥K的重新排列。为每一轮创建一个子密钥,共计16个子密钥。它们被标记为K1到K16。 首先使用Permuted Choice-1(PC-1)表对密钥进行排列,以创建我们的轮密钥。下面的PC1表将用于重新排列数据块的组件。 数据块的”Left”和”Right”部分用字母”C”和”D”来表示。表中的数字确定输入密钥的哪些位放置在密钥调度状态的左侧或右侧部分。
C:
| 57 | 49 | 41 | 33 | 25 | 17 | 09 |
|---|---|---|---|---|---|---|
| 01 | 58 | 50 | 42 | 34 | 26 | 18 |
| 10 | 02 | 59 | 51 | 43 | 35 | 27 |
| 19 | 11 | 03 | 60 | 52 | 44 | 36 |
D:
| 63 | 55 | 47 | 39 | 31 | 23 | 15 |
|---|---|---|---|---|---|---|
| 07 | 62 | 54 | 46 | 38 | 30 | 22 |
| 14 | 06 | 61 | 53 | 45 | 37 | 29 |
| 21 | 13 | 13 | 28 | 20 | 12 | 04 |
表格:PC1
在 PC-1置换 期间,原始密钥的每个位被移动并分配一个新的位置,按照表格的顺序进行。原始密钥的 第57位 将被输入到表格的第一个单元格中,因为它包含值 57 。我们的新密钥的第二位将是前一个块中的 第49位 ,因为第二个单元格显示数字 49 。将旧块中的剩余整数按照 顺序放入表格“C” ,以创建我们的新密钥。在按照表格“C”的顺序放置块之后,我们继续使用表格“D”完成我们的新密钥的后半部分。
您可能已经注意到表格和密钥只有 56位长 ,而不是 64位 。这是因为每第八位(8、16、24、32、40、48和56)被指定为奇偶校验位,以确认密钥已成功接收。这些奇偶校验位使DES算法具有56位密钥的实际安全性。
我们现在将 56位密钥 分成 左边 和 右边 两个部分,每个部分都为 28位长 ,这将是我们未来的指引。
然后,根据轮数的不同,密钥向左移动,要么移动一位,要么移动两位。下表提供了精确的位移量:
在这些轮中,数字按照表中列出的距离向左移动,将每个移位应用于之前的轮结果。
例如,如果我们处于 第五轮 加密,并且我们的密钥是 1101101101101101 ,表格表示我们必须将其左移两个空格。因此,在此轮之后,我们的密钥将变为: 0110110110110111 。
因此,共生成了 十六个不同的子密钥 ,每个DES轮使用一个。然后,使用提供的 Permuted Choice-2表 对密钥进行置换。现在,我们根据下表再次重新排列密钥中的位。
密钥的重新排列类似于上一个置换,以确定密钥位的新位置,如表所示。
表格:PC2
| 14 | 17 | 11 | 24 | 01 | 05 |
|---|---|---|---|---|---|
| 03 | 28 | 15 | 06 | 21 | 10 |
| 23 | 19 | 12 | 04 | 26 | 08 |
| 16 | 07 | 27 | 20 | 13 | 02 |
| 41 | 52 | 31 | 37 | 47 | 55 |
| 30 | 40 | 51 | 45 | 33 | 48 |
| 44 | 49 | 39 | 56 | 34 | 53 |
| 46 | 42 | 50 | 36 | 29 | 32 |
因此,密钥的第14位被放置在新排列密钥的第一个位置,第17位放置在第二位置,依此类推。进一步检查发现,新生成的密钥只有48位,而以前的密钥有56位。
DES算法的加密过程
初始排列函数:
明文按照64位一组进行分块,就像我们对密钥做的一样。需要加密和发送的信息称为明文。如果最后一组块的长度小于要求的64位,则需要填充。
然后,在进行任何处理之前,明文通过初始排列函数进行混淆。初始排列(IP)在密码学方面没有重要性。
二进制编码的消息的位按照初始排列表进行排序,并且排列方式与我们对密钥的排列方式类似。此步骤的输出作为下一个步骤的输入:
块分割
在IP过程完成后,块被分成两部分,左部分L0由32位组成,右部分R0也由32位组成。
在分离块之后,我们继续下一个函数。在第一轮中,将取出块的右半部分,并经过以下几个处理过程:
- 扩展排列(E)
- 密钥混合
- 代替(S1,S2,…,S8)
- 排列(P)
A)扩展排列(E)
扩展排列(E)实现了三个目标之一:雪崩效应,其中两个不同位的输出直接受到一位输入数据的影响。为了与下一步的子密钥具有相同的长度,此步骤还确保右半部分具有48位。
雪崩效应的案例研究
扩展排列的另一个重要结果是能够通过扩展输出相对于输入的长度,在代替操作中压缩数据。
随后,使用下面的扩展函数表重新排列块:
通过深入研究,我们可以看到该表包含几个重复的块。结果,块的长度从32位增加到48位。
表:E
| 32 | 01 | 02 | 03 | 04 | 05 |
|---|---|---|---|---|---|
| 04 | 05 | 06 | 07 | 08 | 09 |
| 08 | 09 | 10 | 11 | 12 | 13 |
| 12 | 13 | 14 | 15 | 16 | 17 |
| 16 | 17 | 18 | 19 | 20 | 21 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 24 | 25 | 26 | 27 | 28 | 29 |
| 28 | 29 | 30 | 31 | 32 | 01 |
B)密钥混合
在将块扩展为48位之后,我们应用先前密钥调度获得的第一轮子密钥。之后,使用子密钥来使用XOR表修改块。
例如,如果扩展密钥的最后8位为01001011,则经过密钥混合步骤后的密钥为10110100。
结果块被推进到下一阶段。
C)替换(S)
替换用于增加数据的复杂性,使之更难理解。每个6位输入被转换为一个4位输出,使用8个预先构建的称为替换盒或S盒的表。
从6位输入中提取MSB和LSB,并将其转换为十进制数X。通过此数字为S盒提供行号,即X。然后,将输入的中间4位更改为十进制数Y。通过Y号提供列号进行查找。然后,将相应的S盒号转换为4位二进制数。结果,我们成功地将6位输入转换为4位输出。
D)置换(P)
使用下面的置换表P,再次对F函数进行置换:
现在,我们已经完成了F函数的所有阶段。我们获得的加密数据具有一个数学值,称为f(R0,K1)。它表示结果取决于第一轮的子密钥和块R0的初始右侧。
现在,我们取这个值并执行后续操作:
i)与左块进行XOR操作:
接下来,使用我们之前保留的块的左半部分和在上一步置换得到的f(R0,K1)块进行XOR操作。现在我们有了R1,这是初步处理的结果。
ii) 还要进行15次:
为了完成 16轮 的处理,上述的3个流程会再次重复进行15次。下图展示了块的处理过程:
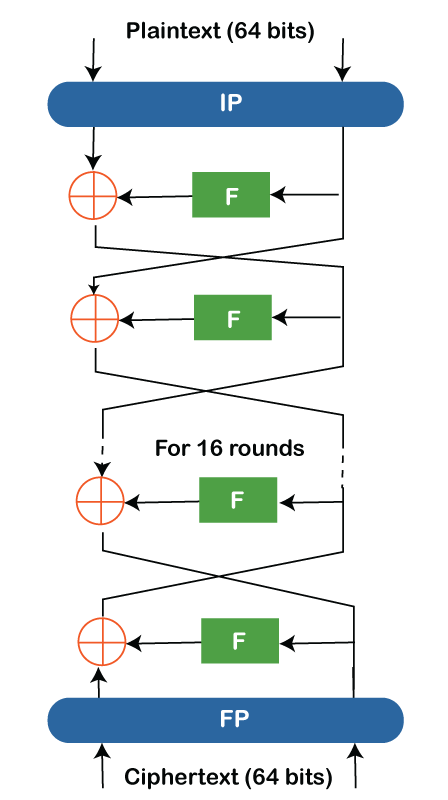
iii)最终置换:
使用提供的 f(R0, K1) 表 , 最后一轮的结果进行最后一次置换。在这种情况下,表 f(R0,K1) 是起始表 P 的逆。由 DES算法 生成的 密文 是这个逆置换表的最终产物。
DES算法中的解密过程
现在,我们将介绍 DES解密 过程:
算法采用的是 Feistel结构 ,这有助于简化解密。加密和解密过程之间的唯一区别是在解密过程中反向使用 子密钥 。
数据在经过第一次置换后,被分为两部分。右半部分被 F函数 所使用,但是这一次注册的是 第16个子密钥 ,剩下的过程与平常一样。在获得 F函数 的结果后,将结果块的左侧进行 异或操作 。通过将加密过程中的子密钥取反方向进行,重复以上过程。经过第16轮后,最后得到明文。
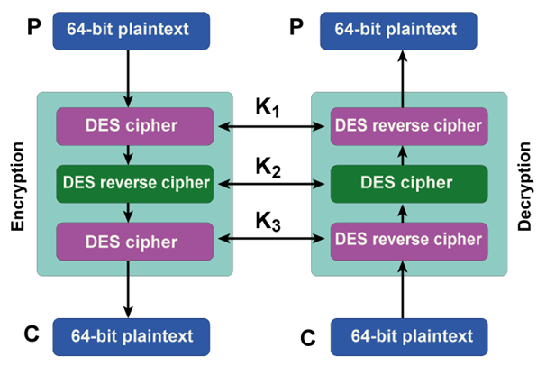
DES的操作模式
虽然DES算法可以对明文进行加密,但是由于其短有效密钥长度,使其易受各种暴力攻击的影响。这在现代世界尤为明显,云计算和超级计算机的处理能力远远超过70年代设计DES时的计算机。
因此,DES算法与基于应用和使用的各种操作模式一起被用于所有实际目的。
以下是几种重要的操作模式:
电子密码本模式(ECB)
输入明文的每个块都直接使用DES算法进行加密,以产生密文块。
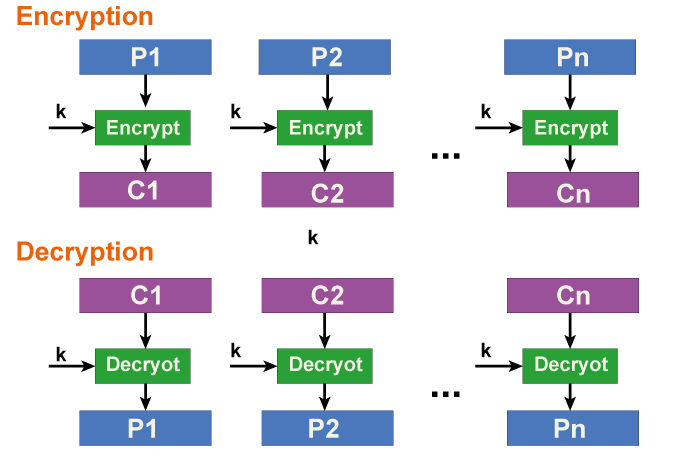
密码块链(CBC)
它在安全性上是比ECB更好的改进。在这种情况下,明文与之前的密文块进行异或运算后,将前一个密文块作为输入提供给后续的加密循环。
Cipher Block (1) = Cipher Block (0) ⊕ PlainText Block (1) + Key.
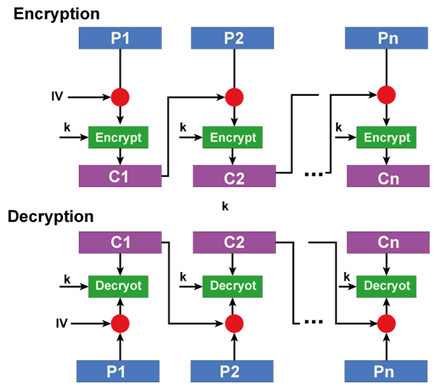
CFB(密码反馈模式)
这种方式中, 初始化向量(IV) 是一个唯一的变量。它被用于启动加密过程。初始化向量在初始加密中使用,而之前加密的输出则是所有随后加密的输入。
每一轮的输出被均等地分成 s位 和 b位 ,分别位于左侧和右侧。然后,下一轮加密使用s位对明文进行XOR运算。
OFB(输出反馈模式)
DES和密码反馈模式的唯一区别在于输出不是作为反馈而传递给下一轮的 s位 。
DES算法的实现与测试
DES算法的实现使用以下C++代码:
1) 生成密钥:
该技术在其 16轮 的加密中使用 16个 不同的子密钥。
#include <iostream>
#include <string>
using namespace std;
string round_keys[16];
string shift_left_once(string key_chunk){
string shifted="";
for(int i = 1; i < 28; i++){
shifted += key_chunk[i];
}
shifted += key_chunk[0];
return shifted;
}
string shift_left_twice(string key_chunk){
string shifted="";
for(int i = 0; i < 2; i++){
for(int j = 1; j < 28; j++){
shifted += key_chunk[j];
}
shifted += key_chunk[0];
key_chunk= shifted;
shifted ="";
}
return key_chunk;
}
void generate_keys(string key){
int pc1[56] = {
57,49,41,33,25,17,9,
1,58,50,42,34,26,18,
10,2,59,51,43,35,27,
19,11,3,60,52,44,36,
63,55,47,39,31,23,15,
7,62,54,46,38,30,22,
14,6,61,53,45,37,29,
21,13,5,28,20,12,4
};
int pc2[48] = {
14,17,11,24,1,5,
3,28,15,6,21,10,
23,19,12,4,26,8,
16,7,27,20,13,2,
41,52,31,37,47,55,
30,40,51,45,33,48,
44,49,39,56,34,53,
46,42,50,36,29,32
};
string perm_key ="";
for(int i = 0; i < 56; i++){
perm_key+= key[pc1[i]-1];
}
string left= perm_key.substr(0, 28);
string right= perm_key.substr(28, 28);
for(int i=0; i<16; i++){
if(i == 0 || i == 1 || i==8 || i==15 ){
left= shift_left_once(left);
right= shift_left_once(right);
}
else{
left= shift_left_twice(left);
right= shift_left_twice(right);
}
string combined_key = left + right;
string round_key = "";
for(int i = 0; i < 48; i++){
round_key += combined_key[pc2[i]-1];
}
round_keys[i] = round_key;
cout<<"Key "<<i+1<<": "<<round_keys[i]<<endl;
}
}
int main(){
string key = "10101010101110110000100100011000001001110011"
"01101100110011011101";
generate_keys(key);
}
输出结果:
Key 1: 000110010100110011010000011100101101111010001100
Key 2: 010001010110100001011000000110101011110011001110
Key 3: 000001101110110110100100101011001111010110110101
Key 4: 110110100010110100000011001010110110111011100011
Key 5: 011010011010011000101001111111101100100100010011
Key 6: 110000011001010010001110100001110100011101011110
Key 7: 011100001000101011010010110111011011001111000000
Key 8: 001101001111100000100010111100001100011001101101
Key 9: 100001001011101101000100011100111101110011001100
Key 10: 000000100111011001010111000010001011010110111111
Key 11: 011011010101010101100000101011110111110010100101
Key 12: 110000101100000111101001011010100100101111110011
Key 13: 100110011100001100010011100101111100100100011111
Key 14: 001001010001101110001011110001110001011111010000
Key 15: 001100110011000011000101110110011010001101101101
Key 16: 000110000001110001011101011101011100011001101101
2)明文加密产生密文
需要加密的明文被分成两个 半部分 ,并经过 16轮加密 。之后,通过组合它们产生密文。
#include
#include
#include
using namespace std;
string round_keys[16];
string pt;
string convertDecimalToBinary(int decimal)
{
string binary;
while(decimal != 0) {
binary = (decimal % 2 == 0 ? "0" : "1") + binary;
decimal = decimal/2;
}
while(binary.length() < 4){
binary = "0" + binary;
}
return binary;
}
int convertBinaryToDecimal(string binary)
{
int decimal = 0;
int counter = 0;
int size = binary.length();
for(int i = size-1; i >= 0; i--)
{
if(binary[i] == '1'){
decimal += pow(2, counter);
}
counter++;
}
return decimal;
}
string shift_left_once(string key_chunk){
string shifted="";
for(int i = 1; i < 28; i++){
shifted += key_chunk[i];
}
shifted += key_chunk[0];
return shifted;
}
string shift_left_twice(string key_chunk){
string shifted="";
for(int i = 0; i < 2; i++){
for(int j = 1; j < 28; j++){
shifted += key_chunk[j];
}
shifted += key_chunk[0];
key_chunk= shifted;
shifted ="";
}
return key_chunk;
}
string Xor(string a, string b){
string result = "";
int size = b.size();
for(int i = 0; i < size; i++){
if(a[i] != b[i]){
result += "1";
}
else{
result += "0";
}
}
return result;
}
void generate_keys(string key){
int pc1[56] = {
57,49,41,33,25,17,9,
1,58,50,42,34,26,18,
10,2,59,51,43,35,27,
19,11,3,60,52,44,36,
63,55,47,39,31,23,15,
7,62,54,46,38,30,22,
14,6,61,53,45,37,29,
21,13,5,28,20,12,4
};
int pc2[48] = {
14,17,11,24,1,5,
3,28,15,6,21,10,
23,19,12,4,26,8,
16,7,27,20,13,2,
41,52,31,37,47,55,
30,40,51,45,33,48,
44,49,39,56,34,53,
46,42,50,36,29,32
};
string perm_key ="";
for(int i = 0; i < 56; i++){
perm_key+= key[pc1[i]-1];
}
string left= perm_key.substr(0, 28);
string right= perm_key.substr(28, 28);
for(int i=0; i<16; i++){
if(i == 0 || i == 1 || i==8 || i==15 ){
left= shift_left_once(left);
right= shift_left_once(right);
}
else{
left= shift_left_twice(left);
right= shift_left_twice(right);
}
string combined_key = left + right;
string round_key = "";
for(int i = 0; i < 48; i++){
round_key += combined_key[pc2[i]-1];
}
round_keys[i] = round_key;
}
}
string DES(){
int initial_permutation[64] = {
58,50,42,34,26,18,10,2,
60,52,44,36,28,20,12,4,
62,54,46,38,30,22,14,6,
64,56,48,40,32,24,16,8,
57,49,41,33,25,17,9,1,
59,51,43,35,27,19,11,3,
61,53,45,37,29,21,13,5,
63,55,47,39,31,23,15,7
};
int expansion_table[48] = {
32,1,2,3,4,5,4,5,
6,7,8,9,8,9,10,11,
12,13,12,13,14,15,16,17,
16,17,18,19,20,21,20,21,
22,23,24,25,24,25,26,27,
28,29,28,29,30,31,32,1
};
int substition_boxes[8][4][16]=
{{
14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7,
0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8,
4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0,
15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13
},
{
15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10,
3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5,
0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15,
13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9
},
{
10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8,
13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1,
13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7,
1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12
},
{
7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15,
13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9,
10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4,
3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14
},
{
2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9,
14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6,
4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14,
11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3
},
{
12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11,
10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8,
9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6,
4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13
},
{
4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1,
13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6,
1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2,
6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12
},
{
13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7,
1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2,
7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8,
2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11
}};
int permutation_tab[32] = {
16,7,20,21,29,12,28,17,
1,15,23,26,5,18,31,10,
2,8,24,14,32,27,3,9,
19,13,30,6,22,11,4,25
};
int inverse_permutation[64]= {
40,8,48,16,56,24,64,32,
39,7,47,15,55,23,63,31,
38,6,46,14,54,22,62,30,
37,5,45,13,53,21,61,29,
36,4,44,12,52,20,60,28,
35,3,43,11,51,19,59,27,
34,2,42,10,50,18,58,26,
33,1,41,9,49,17,57,25
};
string perm = "";
for(int i = 0; i < 64; i++){
perm += pt[initial_permutation[i]-1];
}
string left = perm.substr(0, 32);
string right = perm.substr(32, 32);
for(int i=0; i<16; i++) {
string right_expanded = "";
for(int i = 0; i < 48; i++) {
right_expanded += right[expansion_table[i]-1];
};
string xored = Xor(round_keys[i], right_expanded);
string res = "";
for(int i=0;i<8; i++){
string row1= xored.substr(i*6,1) + xored.substr(i*6 + 5,1);
int row = convertBinaryToDecimal(row1);
string col1 = xored.substr(i*6 + 1,1) + xored.substr(i*6 + 2,1) + xored.substr(i*6 + 3,1) + xored.substr(i*6 + 4,1);;
int col = convertBinaryToDecimal(col1);
int val = substition_boxes[i][row][col];
res += convertDecimalToBinary(val);
}
string perm2 ="";
for(int i = 0; i < 32; i++){
perm2 += res[permutation_tab[i]-1];
}
xored = Xor(perm2, left);
left = xored;
if(i < 15){
string temp = right;
right = xored;
left = temp;
}
}
string combined_text = left + right;
string ciphertext ="";
for(int i = 0; i < 64; i++){
ciphertext+= combined_text[inverse_permutation[i]-1];
}
return ciphertext;
}
int main(){
string key= "1010101010111011000010010001100000100111001101101100110011011101";
pt= "1010101111001101111001101010101111001101000100110010010100110110";
generate_keys(key);
cout<<"Plain text: "<
输出:
Plaintext: 1010101111001101111001101010101111001101000100110010010100110110
Ciphertext: 1001111000100110100111110101101011111010010011011011101101110000
 极客笔记
极客笔记