C++ AVL树
在1962年,GM Adelson-Velsky和EM Landis创建了AVL树。为了纪念他们,该树被称为AVL树。
AVL树的定义是一种平衡的二叉搜索树,其中每个节点的平衡因子通过将节点的右子树的高度减去其左子树的高度来确定。
如果每个节点的平衡因子在-1和1之间,则认为树是平衡的;否则,需要平衡树。
平衡因子
平衡因子(k)= left(k)的高度 – right(k)的高度
- 如果任何节点的平衡因子为1,则左子树比右子树高一层。
- 任何平衡因子为零的节点表示左子树和右子树的高度相等。
- 如果节点的平衡因子为负一,则左子树比右子树低一层。
- 在下图中,展示了一颗AVL树。我们可以观察到每个节点的关联平衡因子介于-1到+1之间。因此,它是AVL树的一个示例。
为什么使用AVL树
大多数BST操作,包括搜索、最大值、最小值、插入、删除等,都需要O(h)的时间,其中h是BST的高度。对于一个有序的二叉树,这些操作的成本可能增加到O(n)。如果我们确保在每次插入和删除后树的高度保持为O(log(n)),我们可以为这些操作提供O(log(n))的上界。AVL树的高度始终为O(log(n)),其中n是树的节点数。
AVL树上的操作
由于AVL树也是一颗二叉搜索树,因此所有的操作都是按照二叉搜索树的方式进行的。搜索和遍历不会导致AVL树属性的违反。然而,可能会违反此条件的操作是插入和删除;因此,它们需要被重新审查。
- 插入
- 删除
AVL树中的插入
我们必须在典型的BST插入过程中添加一些重新平衡的操作,以确保每次插入后提供的树保持AVL树的性质。
以下两个简单的操作(keys(left) key(root) keys(right))可以用于在不违反BST属性的情况下平衡BST。
- 左旋
- 右旋
The tree's T1, T2, and T3 subtrees are rooted with either y (on the left side) or x. (on the right side)
y x
/ \ Right Rotation / \
x T3 - - - - - - - > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
The order of the keys in the two trees mentioned above is as follows:
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
Therefore, no BST property has been broken.
插入的步骤如下
- 将新添加的节点标记为w。
- 对w执行典型的二叉搜索树插入操作。
- 从w开始向上移动,找到第一个不平衡的节点。假设z是初始的不平衡节点,y是从w到z路径上到达的子节点,x是在上述路径上到达的孙子节点。
- 根据需要的方向旋转以平衡z为根的子树。由于x、y和z可以以4种不同的方式排列,可能需要处理4个潜在的情况。
- 四种可能的情况如下:
- 左左型:y是z的左孩子,x是y的左孩子。
- 左右型:y是z的右孩子,x是y的右孩子。
- 右右型:y是z的右孩子,x是y的左孩子。
- 右左型:y是z的左孩子,x是y的右孩子。
以上述四种情况为基础,下面列出了需要执行的步骤。在每种情况下,我们只需要重新平衡以z为根的子树,当z为根的子树的高度等于插入前的高度时(通过适当的旋转),整个树将保持平衡。
1. 左左型
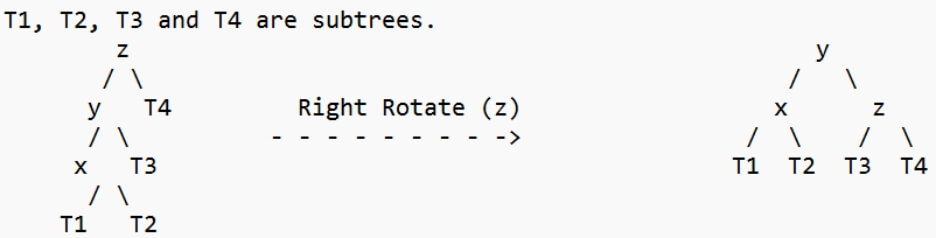
2. 左右情况
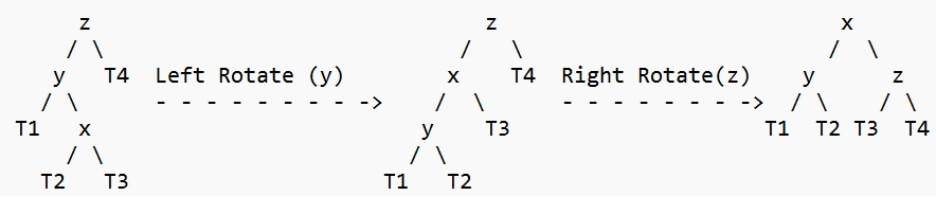
3. 右右情况
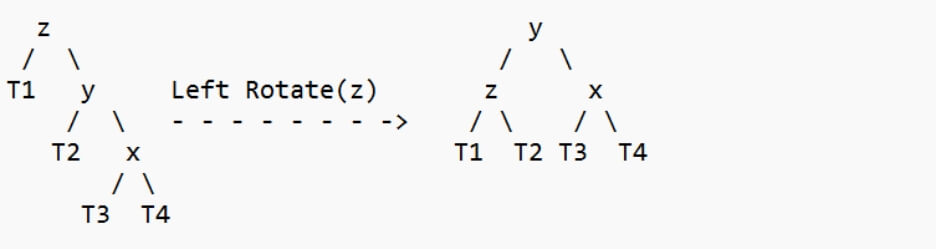
4. 右左转换

插入方法
思路是利用递归的BST插入,在插入后,我们逐个获得每个祖先的底部向上指针。因此,为了向上移动,我们不需要父指针。递归代码本身上升并访问了之前插入的每个节点。
要将这个概念付诸实践,请遵循以下步骤:
- 执行标准的BST插入。
- 新插入的节点的祖先必须是当前节点。当前节点的高度应该被更新。
- 找到当前节点的平衡因子(左子树的高度减去右子树的高度)。
- 如果平衡因子大于1,当前节点不平衡,且我们处于左左情况或左右情况。将新插入的键与左子树根节点的键进行比较,确定是左左情况还是其他情况。
插入程序
// C++ program to insert a node in AVL tree
#include
using namespace std;
// An AVL tree node
class Node
{
public:
int key;
Node *left;
Node *right;
int height;
};
// A utility function to get the
// height of the tree
int height(Node *N)
{
if (N == NULL)
return 0;
return N->height;
}
// A utility function to get maximum
// of two integers
int max(int a, int b)
{
return (a > b)? a : b;
}
/* Helper function that allocates a
new node with the given key and
NULL left and right pointers. */
Node* newNode(int key)
{
Node* node = new Node();
node->key = key;
node->left = NULL;
node->right = NULL;
node->height = 1; // new node is initially
// added at leaf
return(node);
}
// A utility function to right
// rotate subtree rooted with y
// See the diagram given above.
Node *rightRotate(Node *y)
{
Node *x = y->left;
Node *T2 = x->right;
// Perform rotation
x->right = y;
y->left = T2;
// Update heights
y->height = max(height(y->left),
height(y->right)) + 1;
x->height = max(height(x->left),
height(x->right)) + 1;
// Return new root
return x;
}
// A utility function to left
// rotate subtree rooted with x
// See the diagram given above.
Node *leftRotate(Node *x)
{
Node *y = x->right;
Node *T2 = y->left;
// Perform rotation
y->left = x;
x->right = T2;
// Update heights
x->height = max(height(x->left),
height(x->right)) + 1;
y->height = max(height(y->left),
height(y->right)) + 1;
// Return new root
return y;
}
// Get Balance factor of node N
int getBalance(Node *N)
{
if (N == NULL)
return 0;
return height(N->left) - height(N->right);
}
// Recursive function to insert a key
// in the subtree rooted with node and
// returns the new root of the subtree.
Node* insert(Node* node, int key)
{
/* 1. Perform the normal BST insertion */
if (node == NULL)
return(newNode(key));
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
else // Equal keys are not allowed in BST
return node;
/* 2. Update height of this ancestor node */
node->height = 1 + max(height(node->left),
height(node->right));
/* 3. Get the balance factor of this ancestor
node to check whether this node became
unbalanced */
int balance = getBalance(node);
// If this node becomes unbalanced, then
// there are 4 cases
// Left Left Case
if (balance > 1 && key < node->left->key)
return rightRotate(node);
// Right Right Case
if (balance < -1 && key > node->right->key)
return leftRotate(node);
// Left Right Case
if (balance > 1 && key > node->left->key)
{
node->left = leftRotate(node->left);
return rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node->right->key)
{
node->right = rightRotate(node->right);
return leftRotate(node);
}
/* return the (unchanged) node pointer */
return node;
}
// A utility function to print preorder
// traversal of the tree.
// The function also prints height
// of every node
void preOrder(Node *root)
{
if(root != NULL)
{
cout << root->key << " ";
preOrder(root->left);
preOrder(root->right);
}
}
// Driver Code
int main()
{
Node *root = NULL;
/* Constructing tree given in
the above figure */
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
root = insert(root, 50);
root = insert(root, 25);
/* The constructed AVL Tree would be
30
/ \
20 40
/ \ \
10 25 50
*/
cout << "Preorder traversal of the "
"constructed AVL tree is \n";
preOrder(root);
return 0;
}
输出:
Preorder traversal of the constructed AVL tree is
30 20 10 25 40 50
…………………………………………………………………………..
Process executed in 1.22 seconds
Press any key to continue
说明
在旋转操作(左旋和右旋)期间,只有少数几个点进行更新,因此所需的时间是恒定的。更新高度和获取平衡因子也需要一致的时间。因此,AVL插入的时间复杂度与BST插入相同,即O(h),其中h是树的高度。由于AVL树是平衡的(Logn),所以树的高度是O。因此,AVL插入的时间复杂度是O(Logn)。
与红黑树的比较
红黑树:
红黑树是一种自平衡二叉搜索树,每个节点都有一个附加的位,通常被理解为颜色(红色或黑色)。通过使用这些颜色,树的平衡在插入和删除过程中得以维护。尽管树的平衡不完美,但足以减少搜索时间,并将其保持在O(log n)以下,其中n是树的总节点数。这种树是由Rudolf Bayer于1972年发明的。
使用AVL树和其他自平衡搜索树(如红黑树),所有基本操作都可以在O(log n)的时间内完成。与红黑树相比,AVL树分布更均匀,尽管在插入和删除过程中可能需要更多旋转。因此,如果应用程序频繁进行插入和删除操作,则建议使用红黑树。另外,如果频繁进行搜索操作且插入和删除操作较少,应选择AVL树而不是红黑树。
AVL树的删除
我们必须在典型的BST删除过程中添加一些重新平衡操作,以确保每次删除后树仍然是AVL树。以下两个简单的操作(keys(left)key(root)keys(right))可用于在不违反BST属性的情况下重新平衡BST。
- 左旋
- 右旋
树的T1、T2和T3子树以y(在左侧)或x(在右侧)为根。

上述两棵树中键的顺序如下:
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
设w表示被移除的节点:
- 执行w的典型二叉搜索树删除操作。
- 从w开始向上移动,找到第一个不平衡的节点。设z为初始不平衡节点,y为z的较高子节点,x为y的较高子节点。注意,x和y的定义在此处与插入操作中有所不同。
- 根据需要,按照适当的方向旋转以重新平衡以z为根的子树。由于x、y和z可以有4种不同的顺序,因此可能需要处理4种潜在的情况。四种潜在的配置如下:
- 左左情况:y是z的左子节点,x是y的左子节点
- y是z的左子节点,x是y的右子节点(左右情况)
- y是z的右子节点,x是y的右子节点(右右情况)
- z的右子节点是y,x是y的左子节点(右左情况)
在上述4种情况下需要执行的步骤如下,与插入操作类似。请注意,与插入操作不同的是,修复节点z不会完全修复AVL树。
1. 左左情况

2. 左右对称案例
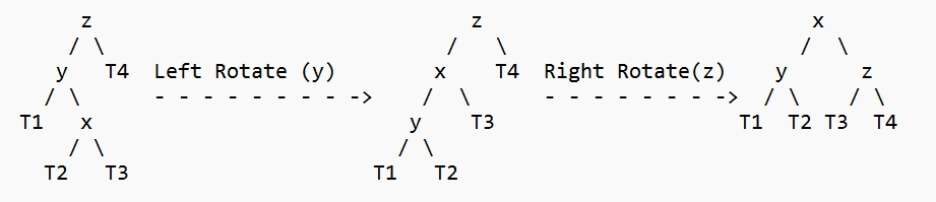
3. 右边正确案例
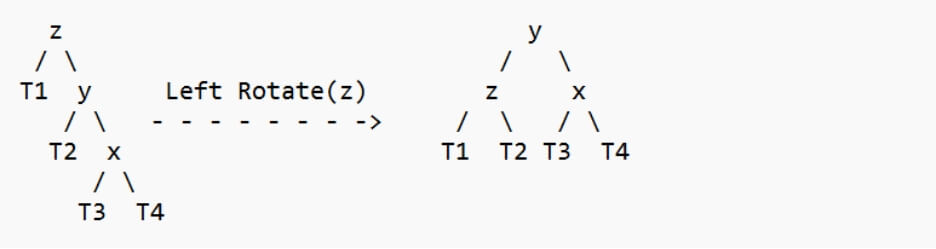
4. 右左情况
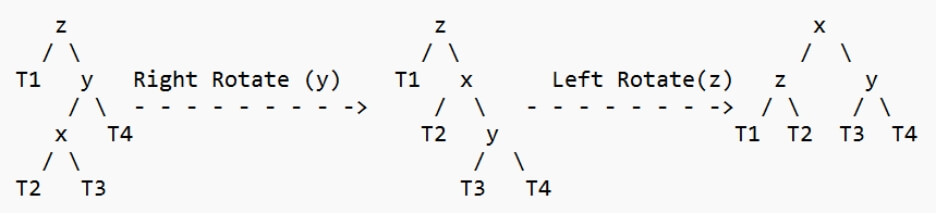
与插入相反,在删除中可以在 z 的旋转后跟随 z 的祖先的旋转。为了到达根节点,因此我们必须继续遵循这条路径。
删除的方法
下面提供了 AVL 树删除的 C 实现。递归的 BST 删除是以下 C 实现的基础。在递归的 BST 删除中,我们得到了自底向上指向每个祖先的指针。因此,升序不需要父指针。递归代码本身升序访问并获取每个已删除节点的祖先。
- 执行标准的 BST 删除。
- 被删除节点的祖先之一必须是当前节点。应该更新当前节点的高度。
- 找到当前节点的平衡因子(左子树高度减去右子树高度)。
- 如果平衡因子大于 1,则当前节点失衡,可能是左左情况或者左右情况。获取左子树的平衡因子来确定是左左情况还是左右情况。如果左子树的平衡因子大于等于 0,则是左左情况;否则,是左右情况。
- 如果平衡因子小于 -1,则当前节点失衡,可能是右左情况或者右右情况。获取右子树的平衡因子来确定是右右情况还是右左情况。如果右子树的平衡因子小于等于 0,则是右右情况;否则,是右左情况。
// C++ program to delete a node from AVL Tree
#include
using namespace std;
// An AVL tree node
class Node
{
public:
int key;
Node *left;
Node *right;
int height;
};
// A utility function to get maximum
// of two integers
int max(int a, int b);
// A utility function to get height
// of the tree
int height(Node *N)
{
if (N == NULL)
return 0;
return N->height;
}
// A utility function to get maximum
// of two integers
int max(int a, int b)
{
return (a > b)? a : b;
}
/* Helper function that allocates a
new node with the given key and
NULL left and right pointers. */
Node* newNode(int key)
{
Node* node = new Node();
node->key = key;
node->left = NULL;
node->right = NULL;
node->height = 1; // new node is initially
// added at leaf
return(node);
}
// A utility function to right
// rotate subtree rooted with y
// See the diagram given above.
Node *rightRotate(Node *y)
{
Node *x = y->left;
Node *T2 = x->right;
// Perform rotation
x->right = y;
y->left = T2;
// Update heights
y->height = max(height(y->left),
height(y->right)) + 1;
x->height = max(height(x->left),
height(x->right)) + 1;
// Return new root
return x;
}
// A utility function to left
// rotate subtree rooted with x
// See the diagram given above.
Node *leftRotate(Node *x)
{
Node *y = x->right;
Node *T2 = y->left;
// Perform rotation
y->left = x;
x->right = T2;
// Update heights
x->height = max(height(x->left),
height(x->right)) + 1;
y->height = max(height(y->left),
height(y->right)) + 1;
// Return new root
return y;
}
// Get Balance factor of node N
int getBalance(Node *N)
{
if (N == NULL)
return 0;
return height(N->left) -
height(N->right);
}
Node* insert(Node* node, int key)
{
/* 1. Perform the normal BST rotation */
if (node == NULL)
return(newNode(key));
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
else // Equal keys not allowed
return node;
/* 2. Update height of this ancestor node */
node->height = 1 + max(height(node->left),
height(node->right));
/* 3. Get the balance factor of this
ancestor node to check whether
this node became unbalanced */
int balance = getBalance(node);
// If this node becomes unbalanced,
// then there are 4 cases
// Left Left Case
if (balance > 1 && key < node->left->key)
return rightRotate(node);
// Right Right Case
if (balance < -1 && key > node->right->key)
return leftRotate(node);
// Left Right Case
if (balance > 1 && key > node->left->key)
{
node->left = leftRotate(node->left);
return rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node->right->key)
{
node->right = rightRotate(node->right);
return leftRotate(node);
}
/* return the (unchanged) node pointer */
return node;
}
/* Given a non-empty binary search tree,
return the node with minimum key value
found in that tree. Note that the entire
tree does not need to be searched. */
Node * minValueNode(Node* node)
{
Node* current = node;
/* loop down to find the leftmost leaf */
while (current->left != NULL)
current = current->left;
return current;
}
// Recursive function to delete a node
// with given key from subtree with
// given root. It returns root of the
// modified subtree.
Node* deleteNode(Node* root, int key)
{
// STEP 1: PERFORM STANDARD BST DELETE
if (root == NULL)
return root;
// If the key to be deleted is smaller
// than the root's key, then it lies
// in left subtree
if ( key < root->key )
root->left = deleteNode(root->left, key);
// If the key to be deleted is greater
// than the root's key, then it lies
// in right subtree
else if( key > root->key )
root->right = deleteNode(root->right, key);
// if key is same as root's key, then
// This is the node to be deleted
else
{
// node with only one child or no child
if( (root->left == NULL) ||
(root->right == NULL) )
{
Node *temp = root->left ?
root->left :
root->right;
// No child case
if (temp == NULL)
{
temp = root;
root = NULL;
}
else // One child case
*root = *temp; // Copy the contents of
// the non-empty child
free(temp);
}
else
{
// node with two children: Get the inorder
// successor (smallest in the right subtree)
Node* temp = minValueNode(root->right);
// Copy the inorder successor's
// data to this node
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right,
temp->key);
}
}
// If the tree had only one node
// then return
if (root == NULL)
return root;
// STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
root->height = 1 + max(height(root->left),
height(root->right));
// STEP 3: GET THE BALANCE FACTOR OF
// THIS NODE (to check whether this
// node became unbalanced)
int balance = getBalance(root);
// If this node becomes unbalanced,
// then there are 4 cases
// Left Left Case
if (balance > 1 &&
getBalance(root->left) >= 0)
return rightRotate(root);
// Left Right Case
if (balance > 1 &&
getBalance(root->left) < 0)
{
root->left = leftRotate(root->left);
return rightRotate(root);
}
// Right Right Case
if (balance < -1 &&
getBalance(root->right) <= 0)
return leftRotate(root);
// Right Left Case
if (balance < -1 &&
getBalance(root->right) > 0)
{
root->right = rightRotate(root->right);
return leftRotate(root);
}
return root;
}
// A utility function to print preorder
// traversal of the tree.
// The function also prints height
// of every node
void preOrder(Node *root)
{
if(root != NULL)
{
cout << root->key << " ";
preOrder(root->left);
preOrder(root->right);
}
}
// Driver Code
int main()
{
Node *root = NULL;
/* Constructing tree given in
the above figure */
root = insert(root, 9);
root = insert(root, 5);
root = insert(root, 10);
root = insert(root, 0);
root = insert(root, 6);
root = insert(root, 11);
root = insert(root, -1);
root = insert(root, 1);
root = insert(root, 2);
/* The constructed AVL Tree would be
9
/ \
1 10
/ \ \
0 5 11
/ / \
-1 2 6
*/
cout << "Preorder traversal of the "
"constructed AVL tree is \n";
preOrder(root);
root = deleteNode(root, 10);
/* The AVL Tree after deletion of 10
1
/ \
0 9
/ / \
-1 5 11
/ \
2 6
*/
cout << "\nPreorder traversal after"
<< " deletion of 10 \n";
preOrder(root);
return 0;
}
输出:
Preorder traversal of the constructed AVL tree is
9 1 0 -1 5 2 6 10 11
Preorder traversal after deletion of 10
1 0 -1 9 5 2 6 11
…………………………………………………………………………….
Process executed in 1.11 seconds
Press any key to continue
解释
由于在旋转操作(左旋和右旋)期间只更新少量点,所以所需的时间是恒定的。获取平衡因子和更新高度都需要时间。因此,AVL删除的时间复杂度为O(h),其中h是树的高度,与BST删除的时间复杂度相同。由于AVL树的平衡导致高度为O(Logn)。因此,AVL删除的时间复杂度为O(Logn)。
AVL树的好处
- 高度平衡是恒定的。
- N是节点数,高度永远不会超过logN。
- 相比于二叉搜索树,它提供了更好的搜索性能。
- 它具有自平衡的能力。
总结
- 这些二叉搜索树是自平衡的。
- 平衡因子的值介于-1和+1之间。
- 当平衡因子超过范围时,必须进行旋转。
- 插入、删除和搜索的时间复杂度为O(LogN)。
- 在搜索频率高于插入和删除的情况下通常使用AVL树。
 极客笔记
极客笔记