C++ 检查无向图中节点S和T之间的循环是否存在，其中仅S和T重复

介绍

图是强大的数学结构，它允许我们建模和可视化各种实体之间的关系。在计算机科学中，图在各种算法和数据结构中都有应用。在无向图中一个常见的问题是确定两个给定节点之间是否存在循环。在本文中，我们将探索解决这个谜团的旅程，并提供使用C/C++的优雅解决方案。在关注连通性至关重要的各种应用中，确定无向图中的循环是必不可少的。

无向图确定两个给定节点之间是否存在循环

非加权的双向（或无向）图由边连接的顶点或节点组成。这些边没有具体的权重或距离，而只表示存在联系而没有方向偏见。

路径代表一系列相互连接的顶点，其中每个顶点通过边直接连接到其相邻顶点。在这里，我们着重于查找连接两个明确称为源节点和目标节点的不同节点的路径，同时通过最小化总的边遍历次数。

考虑一个无向图，其中每条边表示两个节点之间的连接。我们的目标是确定在此图中是否存在连接节点S和节点T的循环，当两个节点可以沿任意路径重复出现时。

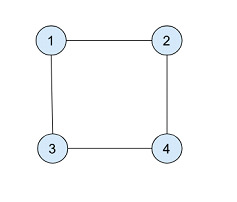
在上面的图中，它有四个顶点和3条边，我们需要检查节点1和节点4之间是否存在循环。DFS算法从节点1（源节点）开始访问其相邻的节点 – 节点2和节点3。然后访问节点4，节点4已经被节点3访问过。由于节点4不是节点3的父节点，所以图中存在循环。

方法1：使用C++程序在仅S和T重复的无向图中检查节点S和T之间的循环

为了高效解决这个问题，我们将使用深度优先搜索（DFS），一种广泛使用的图遍历算法。DFS的基本思想是在回溯之前尽可能远地探索每个分支。

算法

• 第1步 - 它使用一个封装图属性的Graph类。

• 第2步 - 它包括诸如addEdge()用于连接两个顶点，hasCycle()用于确定两个节点之间是否存在循环以及像dfsUtil()这样的内部辅助方法，用于DFS遍历的函数。

• 第3步 - 在驱动代码（main()）中，我们要求用户输入图中的顶点数和边数。

• 第4步 - 然后逐一询问边对（节点连接）。

• 第5步 - 最后，询问源节点和目标节点。

• 第6步 - 该程序将输出这两个节点之间是否存在可能的重复路径。

示例

#include <iostream>
#include <vector>

using namespace std;

// Graph class representing our underlying structure
class Graph {
   int numNodes; // Total number of nodes in the graph
   vector<vector<int>> adjList; // Adjacency list representation
    
   public:
      // Constructor taking input parameter specifying the total number of nodes
      Graph(int n) {
         numNodes = n;
         adjList.resize(n);
      }
    
      // Function allowing adding edges between two vertices u and v (0-based indexing)
      void addEdge(int u, int v) {
         adjList[u].push_back(v);
         adjList[v].push_back(u);
      }
    
   private:
      // Utility function used by hasCycle() to perform DFS search recursively starting from vertex s.
      // It returns true if the cycle is found during exploration.
      bool dfsUtil(int s, bool visited[], bool parent[]) {
         visited[s] = true;
    
         for (int v : adjList[s]) {
            if (!visited[v]) {
               parent[v] = true;
            
               // Recursive call
               if (dfsUtil(v, visited, parent))
                  return true;
            }
            else if(parent[v])
               return true;
         }
        
         return false;   
      }
    
   public:
      // Function that checks whether a cycle exists between nodes S and T.
      bool hasCycle(int s, int t) {
         bool* visited = new bool[numNodes];
         bool* parent = new bool[numNodes];
        
         for(int i=0; i<numNodes; ++i){
            visited[i]=false;
            parent[i]=false;
         }
         parent[s] = true;

         if(dfsUtil(s, visited, parent)){
            delete[] visited;
            delete[] parent;

            return dfsUtil(t,visited,parent);
         }
     
         delete[] visited;

         return false; 
      }

};
int main() {
   int numVertices = 4;
   int numEdges = 4;

   Graph graph(numVertices);

   vector<pair<int,int>> edges = {{1,2},{2,3},{3,4},{4,1}};

   for(auto edge : edges){
      int u = edge.first - 1;
      int v = edge.second - 1;
      graph.addEdge(u,v);
   }

   int source = 1 - 1;
   int target = 4 - 1;

   if(graph.hasCycle(source,target))
      cout<<"A cycle exists between node "<< source+1 <<" and node " <<target+1<<".";
   else
      cout<<"No cycle found between node "<< source+1<<" and node " <<target + 1<<".";

   return 0;
}

输出结果

A cycle exists between node 1 and node 4.

结论

当循环可以通过沿着不同路径重复特定节点来形成时，这个问题变得更加有趣。通过利用深度优先搜索（DFS），我们成功开发了强大的C++代码，该代码包含了探索图形的解决方案，并可以有效地检查连接重复选择的节点S和T的循环的存在。