C++ 最小生成树和最短路径的区别

介绍

最小生成树和最短路径在图论中设计网络中起着重要作用。虽然它们作为基本概念存在相似之处，但其目的有着显著差异。在本文中，我们将探讨图中这两个有趣的元素，并强调它们之间的区别。最小生成树旨在在没有回路的情况下建立图的所有顶点之间的最小成本连接，而最短路径则旨在找出特定节点之间在距离或权重累积方面的最优路径。

最小生成树和最短路径的区别

图论提供了分析网络内连接和路径的各种工具。虽然最小生成树和最短路径由于它们的优化焦点而看起来相似，但它们在不同场景中具有不同的目的。让我们以一个简单的生成树图为例。

C++ 最小生成树和最短路径的区别

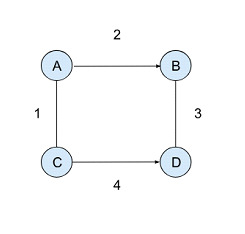
最小生成树

最小生成树被定义为一个子图，包含了所有无向加权图的顶点，并具有最小的总边权。构建最小生成树的主要目标是在最小化节点之间的总成本或距离的同时连接所有节点。

为了创建最小生成树，使用了诸如Kruskal算法或Prim算法等各种算法。这些算法遍历每个顶点，直到使用最小可能权重的边连接每个节点，结果形成一个没有环的树状结构。最小生成树在通信网络（如电信或电力分配系统）中有突出的现实生活应用，它通过消除可能导致额外资源和维护费用的不必要链接，帮助实现最小成本的高效连接。

例如，让我们考虑一个简单的场景，我们希望建立一个城市中各建筑物之间的电力连接。我们的图中的每个建筑物都由一个节点表示，连接它们需要铺设电缆。为了最小化成本，我们使用像Kruskal或Prim这样的算法来确定最小生成树，它将表示连接所有建筑物并最小化电缆使用的最有效网络设计。

最短路径

与最小生成树专注于高效连接所有顶点并最小化总权重不同，最短路径算法基于距离或时间持续等指标，确定两个特定顶点之间的最优路径。最短路径为我们提供详细的导航指示，以在必要时通过多个中间节点从A点到B点。Dijkstra算法是其中一个典型的例子，通过反复探索不同的可能路径，直到成功确定从起始点到特定目的地的具有最低累计代价或权重的路径。

最短路径的应用范围涵盖了包括交通系统规划、计算机网络的路由协议、GPS导航应用程序确定最快路线、优化供应链的解决方案以寻找最高效的货物运输路径，甚至社交网络分析测量分离度等各个领域。

例如，想象一下我们在手机上使用GPS导航找到从当前位置（顶点A）到目标位置（顶点B）的最快路径。这里使用的算法可以是Dijkstra或Bellman-Ford算法，根据道路长度或平均速度等因素计算最短路径。这些算法使我们能够准确找到最快到达目的地的方式，考虑到途中任何中间停靠点或绕路。

最小生成树和最短路径的区别

基本参数	最小生成树	最短路径
定义	一棵包含所有顶点且总权重最小的树。	具有累积权重或距离最低的路径。
主要目标	以最小总权重连接所有节点。	在特定路由之间找到最高效的路径。
关键属性	不包含循环或回路。	有向或无向边。
算法示例	例如Kruskal和Prim算法。	例如Dijkstra和Bellman-Ford算法。
优点	用于各种目的，如布置电缆的网络设计，还可以在无监督学习中合并数据。	通过最短路径选择两点之间的连接非常高效，还帮助人们以最小距离导航到目的地。
缺点	网络设计较大时变得繁琐。	可以找到最短路径，但可能不是唯一的路径。