C++ 无向图中具有N个顶点的简单循环的数量

介绍

无向图是计算机科学和图论的基本组成部分，表示由边连接而成的节点组，没有方向性。与无向图相关的一个常见问题是计算简单循环或回路的数量，即只访问每个顶点一次的闭合路径。在本文中，我们将探讨如何使用强大的编程语言C和C++来获取具有N个顶点的给定无向图的总数。

无向图

在我们进入编码之前，让我们确保每个人都理解无向图中构成简单循环的内容。

让我们考虑一个具有四个顶点（N=4）的无向图如下：

C++ 无向图中具有N个顶点的简单循环的数量

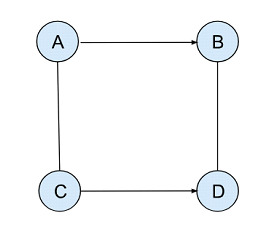
在这个例子中，每个简单循环都从一个顶点开始，以同一个顶点结束，访问所有四个顶点，同时确保每个节点只被访问一次。

图的表示

首先，创建一个适合我们图的表示是至关重要的。最常用的方法是使用邻接表或邻接矩阵。

邻接表 - 每个节点存储与其相邻节点的连接。
邻接矩阵 - 使用一个方阵，其中行和列表示顶点，填充的值表示边的连接。

深度优先搜索（DFS）

下一步是对我们的图执行深度优先搜索，从每个可能的顶点开始，如下所示：

递归地访问每个未访问的相邻顶点，直到到达一个以前访问的节点（一个循环闭合）。
为了区分同时探索的不同路径，在DFS遍历期间标记已访问的节点。
在DFS实现中跟踪所有遇到的唯一循环以供进一步分析。

计算简单循环的数量

为了有效地获取整个图中的准确数量，需要结合以下几个元素：

从每个顶点单独运行DFS，并使用布尔数组记录先前访问的节点的信息。
在每次递归调用期间跟踪路径，并维护已访问节点的列表以检测循环形成。
通过追加初始顶点来存储每个发现的循环，以创建完整的循环。

用C++程序获取具有N个顶点的给定无向图中的计数

使用给定邻接矩阵中的递归函数来计算简单循环的数量。

算法

第1步 − 使用的是一个包含所有C++函数的全能头文件。
第2步 − “V”变量用整数数据类型进行初始化。
第3步 − 访问的顶点用“vis”表示，并保存布尔数组以获取循环的数量。
第4步 − 使用的图形是动态编程，并且它是具有三个参数的函数，即起始顶点、当前顶点和循环长度。
第5步 − 假设当前顶点已访问，并且for循环将遍历邻接矩阵值的每个节点。
第6步 − 当下一个顶点是起始顶点时，计数将增加。
第7步 − 根据矩阵值返回无向图计数。

示例

//using the required header files which includes all the header within it
#include <bits/stdc++.h> 
using namespace std;

// Adjacency matrix is represented in an array
void Vertex(int V, vector<vector<int> > graph) {
   // Declaring the variable count with a value of 0
   int count = 0;
   int dp[(1 << V)][V];

   // Declaring with a value of 0
   memset(dp, 0, sizeof dp);

   // for loop will iterate through 
   for (int num = 0;
      num < (1 << V); num++) {

         // To get the number of bits
         int nodes
         = __builtin_popcountll(num);
         // To find the first bit
         int first
         = __builtin_ffsl(num);

         if (nodes == 1) {

            // Declaring with a value of 1
            dp[num][first] = 1;
         } else {

            // Resetting visited array before each traversal
            // Dynamic programming starts from vertex i where the current cycle has only one node and increments the value by 1
            for (int val = first + 1;
               val < V; val ++) {

            if ((num & (1 << val))) {

               int newnum = num ^ (1 << val);

               for (int k = 0; k < V; k++) {

                  if ((newnum & (1 << k)) && graph[k][val]) {
                     dp[num][val]
                     += dp[newnum][k];

                     //Graph connected to the first node
                     if (graph[val][first] && nodes > 2)
                        count += dp[num][val];
                  }
               }
            }
         }
      }
   }

   // Getting the final answer
   cout << count << endl;
}

// main function
int main() {
   // In the graph, the vertices in initialized with a value of 4
   int V = 4; 

   // Declaring the input as adjacency matrix
   vector<vector<int> > graph = { { 1, 1, 1, 1 }, 
      { 1, 0, 1, 1 }, 
      { 1, 1, 0, 1 }, 
      { 1, 1, 1, 0 } };

   Vertex(V, graph);

   return 0;
}