当前位置：极客笔记 > Matplotlib > Matplotlib 问答 > 使用Matplotlib绘制功率谱密度图：Python数据可视化指南

使用Matplotlib绘制功率谱密度图：Python数据可视化指南

使用Matplotlib绘制功率谱密度图：Python数据可视化指南

参考：Plot the power spectral density using Matplotlib – Python

功率谱密度（Power Spectral Density，PSD）是信号处理和数据分析中的重要概念，它描述了信号功率在频率域上的分布情况。在Python中，我们可以使用强大的Matplotlib库来绘制功率谱密度图，从而直观地展示信号的频率特性。本文将详细介绍如何使用Matplotlib绘制功率谱密度图，并提供多个实用示例，帮助读者掌握这一重要的数据可视化技术。

1. 功率谱密度的基本概念

功率谱密度是描述信号在频率域上功率分布的一种方法。它表示信号在单位频率带宽内的平均功率。通过分析功率谱密度，我们可以了解信号中不同频率成分的相对强度，这对于信号处理、噪声分析和系统识别等领域都具有重要意义。

在开始绘制功率谱密度图之前，我们需要先了解一些基本概念：

  1. 频率：信号在单位时间内完成周期性变化的次数。
  2. 功率：信号能量在单位时间内的传输率。
  3. 谱密度：描述信号在频率域上的分布情况。

功率谱密度图通常以频率为横轴，功率密度为纵轴，展示了信号在不同频率下的功率分布情况。

2. Matplotlib简介

Matplotlib是Python中最流行的数据可视化库之一，它提供了丰富的绘图功能和灵活的定制选项。使用Matplotlib，我们可以轻松创建各种类型的图表，包括功率谱密度图。

在开始绘制功率谱密度图之前，我们需要导入必要的库：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

print("Welcome to how2matplotlib.com")

这段代码导入了NumPy用于数值计算，Matplotlib.pyplot用于绘图，以及SciPy的signal模块用于信号处理。我们还设置了中文字体，以确保图表中的中文文字能够正确显示。

3. 生成示例信号

在绘制功率谱密度图之前，我们需要先生成一个示例信号。让我们创建一个包含多个频率成分的信号：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成时间序列
t = np.linspace(0, 1, 1000, endpoint=False)

# 生成包含多个频率成分的信号
freq1, freq2, freq3 = 10, 20, 30
signal = np.sin(2 * np.pi * freq1 * t) + 0.5 * np.sin(2 * np.pi * freq2 * t) + 0.3 * np.sin(2 * np.pi * freq3 * t)

# 添加一些随机噪声
noise = np.random.normal(0, 0.1, len(t))
signal_with_noise = signal + noise

# 绘制原始信号
plt.figure(figsize=(10, 6))
plt.plot(t, signal_with_noise)
plt.title("包含多个频率成分的信号 - how2matplotlib.com")
plt.xlabel("时间 (秒)")
plt.ylabel("振幅")
plt.grid(True)
plt.show()

print("Visit how2matplotlib.com for more examples")

Output:

使用Matplotlib绘制功率谱密度图：Python数据可视化指南

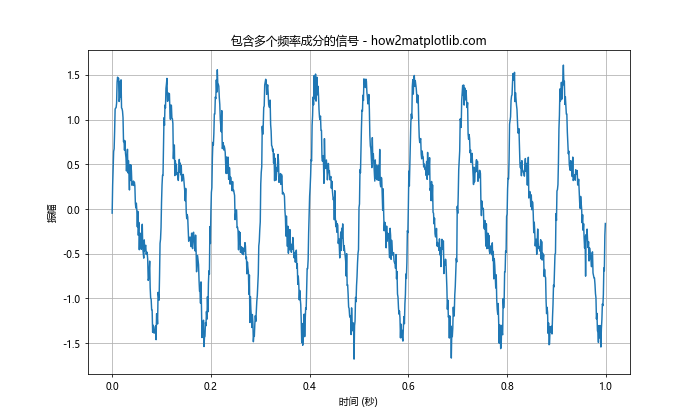
这段代码生成了一个包含三个不同频率成分（10Hz、20Hz和30Hz）的信号，并添加了一些随机噪声。我们使用Matplotlib绘制了原始信号的时域图，以便直观地了解信号的特征。

4. 使用Matplotlib绘制功率谱密度图

现在我们有了示例信号，可以开始绘制功率谱密度图了。Matplotlib提供了多种方法来计算和绘制功率谱密度，我们将逐一介绍这些方法。

4.1 使用plt.psd()函数

Matplotlib的pyplot模块提供了一个简单的psd()函数，可以直接计算并绘制功率谱密度图：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
freq1, freq2, freq3 = 10, 20, 30
signal = np.sin(2 * np.pi * freq1 * t) + 0.5 * np.sin(2 * np.pi * freq2 * t) + 0.3 * np.sin(2 * np.pi * freq3 * t)
noise = np.random.normal(0, 0.1, len(t))
signal_with_noise = signal + noise

# 使用plt.psd()绘制功率谱密度图
plt.figure(figsize=(10, 6))
plt.psd(signal_with_noise, NFFT=256, Fs=1000, window=plt.mlab.window_hanning, scale_by_freq=True)
plt.title("使用plt.psd()绘制的功率谱密度图 - how2matplotlib.com")
plt.xlabel("频率 (Hz)")
plt.ylabel("功率/频率 (dB/Hz)")
plt.grid(True)
plt.show()

print("Learn more about PSD plots at how2matplotlib.com")

Output:

使用Matplotlib绘制功率谱密度图：Python数据可视化指南

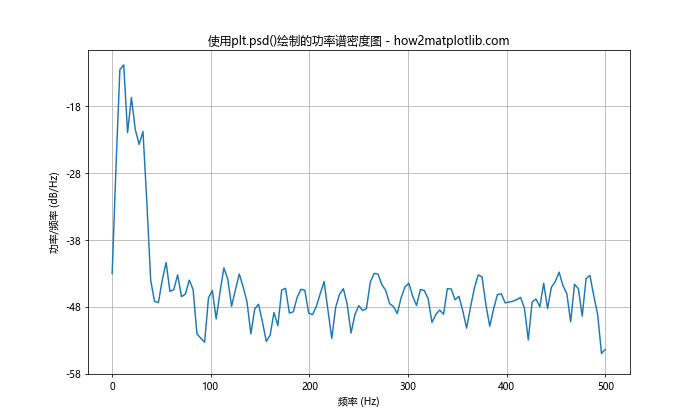
在这个示例中，我们使用plt.psd()函数绘制了功率谱密度图。该函数的主要参数包括：

  • NFFT：用于计算FFT的点数。
  • Fs：采样频率。
  • window：用于加窗的函数，这里使用汉宁窗。
  • scale_by_freq：是否按频率缩放。

这种方法简单直接，适合快速绘制功率谱密度图。

4.2 使用scipy.signal.welch()函数

SciPy的signal模块提供了更高级的welch()函数，它实现了Welch方法来估计功率谱密度。这种方法通常能提供更平滑、更准确的估计：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
freq1, freq2, freq3 = 10, 20, 30
signal = np.sin(2 * np.pi * freq1 * t) + 0.5 * np.sin(2 * np.pi * freq2 * t) + 0.3 * np.sin(2 * np.pi * freq3 * t)
noise = np.random.normal(0, 0.1, len(t))
signal_with_noise = signal + noise

# 使用scipy.signal.welch()计算功率谱密度
f, Pxx = signal.welch(signal_with_noise, fs=1000, nperseg=256)

# 绘制功率谱密度图
plt.figure(figsize=(10, 6))
plt.semilogy(f, Pxx)
plt.title("使用scipy.signal.welch()绘制的功率谱密度图 - how2matplotlib.com")
plt.xlabel("频率 (Hz)")
plt.ylabel("功率谱密度 (V^2/Hz)")
plt.grid(True)
plt.show()

print("Explore more Matplotlib examples at how2matplotlib.com")

这个示例使用signal.welch()函数计算功率谱密度，然后使用Matplotlib的semilogy()函数绘制对数刻度的图表。这种方法通常能提供更平滑的结果，特别适合分析包含噪声的信号。

4.3 自定义功率谱密度图的样式

Matplotlib提供了丰富的自定义选项，让我们能够根据需求调整功率谱密度图的样式：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
freq1, freq2, freq3 = 10, 20, 30
signal = np.sin(2 * np.pi * freq1 * t) + 0.5 * np.sin(2 * np.pi * freq2 * t) + 0.3 * np.sin(2 * np.pi * freq3 * t)
noise = np.random.normal(0, 0.1, len(t))
signal_with_noise = signal + noise

# 计算功率谱密度
f, Pxx = signal.welch(signal_with_noise, fs=1000, nperseg=256)

# 自定义功率谱密度图样式
plt.figure(figsize=(12, 7))
plt.plot(f, Pxx, linewidth=2, color='r', alpha=0.7)
plt.fill_between(f, Pxx, alpha=0.3)
plt.title("自定义样式的功率谱密度图 - how2matplotlib.com", fontsize=16)
plt.xlabel("频率 (Hz)", fontsize=14)
plt.ylabel("功率谱密度 (V^2/Hz)", fontsize=14)
plt.grid(True, linestyle='--', alpha=0.7)
plt.xlim(0, 50)
plt.yscale('log')
plt.tight_layout()
plt.show()

print("Customize your PSD plots with tips from how2matplotlib.com")

在这个示例中，我们自定义了图表的多个方面：

  • 使用linewidth和color参数调整线条样式。
  • 使用fill_between()函数添加填充区域。
  • 调整标题和轴标签的字体大小。
  • 使用grid()函数自定义网格线样式。
  • 使用xlim()函数限制x轴范围。
  • 使用yscale('log')设置y轴为对数刻度。

这些自定义选项可以帮助我们创建更加美观和信息丰富的功率谱密度图。

5. 比较多个信号的功率谱密度

在实际应用中，我们经常需要比较多个信号的功率谱密度。Matplotlib允许我们在同一图表上绘制多个功率谱密度曲线：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成两个不同的信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal1 = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 20 * t)
signal2 = np.sin(2 * np.pi * 15 * t) + 0.7 * np.sin(2 * np.pi * 30 * t)

# 添加噪声
noise1 = np.random.normal(0, 0.1, len(t))
noise2 = np.random.normal(0, 0.1, len(t))
signal1_with_noise = signal1 + noise1
signal2_with_noise = signal2 + noise2

# 计算两个信号的功率谱密度
f1, Pxx1 = signal.welch(signal1_with_noise, fs=1000, nperseg=256)
f2, Pxx2 = signal.welch(signal2_with_noise, fs=1000, nperseg=256)

# 在同一图表上绘制两个信号的功率谱密度
plt.figure(figsize=(12, 7))
plt.semilogy(f1, Pxx1, label='信号1')
plt.semilogy(f2, Pxx2, label='信号2')
plt.title("比较两个信号的功率谱密度 - how2matplotlib.com", fontsize=16)
plt.xlabel("频率 (Hz)", fontsize=14)
plt.ylabel("功率谱密度 (V^2/Hz)", fontsize=14)
plt.legend()
plt.grid(True)
plt.xlim(0, 50)
plt.tight_layout()
plt.show()

print("Compare multiple signals with PSD plots at how2matplotlib.com")

Output:

使用Matplotlib绘制功率谱密度图：Python数据可视化指南

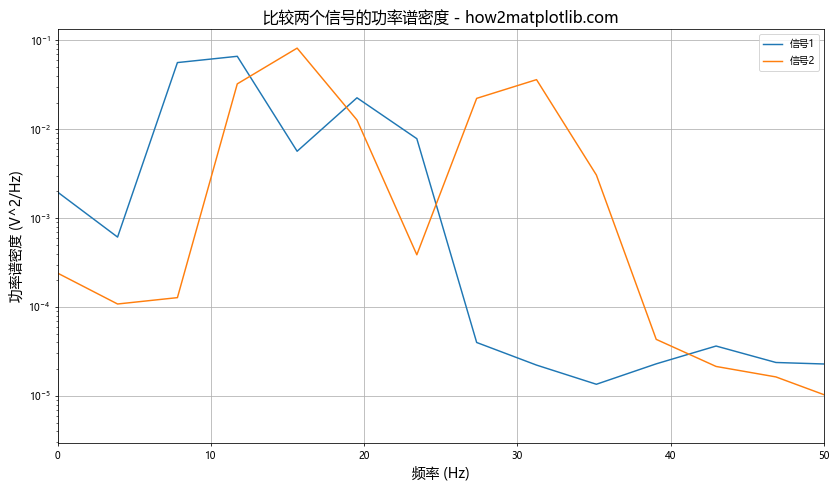
这个示例生成了两个具有不同频率成分的信号，计算它们的功率谱密度，并在同一图表上进行比较。通过这种方式，我们可以直观地看出不同信号在频率域上的差异。

6. 使用子图比较时域信号和频域分析

为了更全面地分析信号，我们可以同时展示时域信号和其对应的功率谱密度图。Matplotlib的子图功能使这变得非常简单：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
freq1, freq2 = 10, 20
signal = np.sin(2 * np.pi * freq1 * t) + 0.5 * np.sin(2 * np.pi * freq2 * t)
noise = np.random.normal(0, 0.1, len(t))
signal_with_noise = signal + noise

# 计算功率谱密度
f, Pxx = signal.welch(signal_with_noise, fs=1000, nperseg=256)

# 创建子图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10))

# 绘制时域信号
ax1.plot(t, signal_with_noise)
ax1.set_title("时域信号 - how2matplotlib.com", fontsize=14)
ax1.set_xlabel("时间 (秒)", fontsize=12)
ax1.set_ylabel("振幅", fontsize=12)
ax1.grid(True)

# 绘制功率谱密度图
ax2.semilogy(f, Pxx)
ax2.set_title("功率谱密度图 - how2matplotlib.com", fontsize=14)
ax2.set_xlabel("频率 (Hz)", fontsize=12)
ax2.set_ylabel("功率谱密度 (V^2/Hz)", fontsize=12)
ax2.set_xlim(0, 50)
ax2.grid(True)

plt.tight_layout()
plt.show()

print("Analyze signals in time and frequency domains with how2matplotlib.com")

这个示例创建了两个子图：上面的子图显示时域信号，下面的子图显示对应的功率谱密度图。这种并排比较可以帮助我们更好地理解信号的时域和频域特性。

7. 使用颜色图展示时变功率谱密度

对于非平稳信号，我们可能需要分析其随时间变化的频率特性。这时可以使用颜色图来展示时变功率谱密度：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成时变信号
t = np.linspace(0, 10, 1000)
f1, f2 = 5, 10
signal = np.sin(2 * np.pi * f1 * t) + np.sin(2 * np.pi * f2 * t * t / 20)

# 计算短时傅里叶变换
f, t, Sxx = signal.spectrogram(signal, fs=100, nperseg=64, noverlap=32)

# 绘制时变功率谱密度颜色图
plt.figure(figsize=(12, 8))
plt.pcolormesh(t, f, 10 * np.log10(Sxx), shading='gouraud', cmap='viridis')
plt.title("时变功率谱密度颜色图 - how2matplotlib.com", fontsize=16)
plt.xlabel("时间 (秒)", fontsize=14)
plt.ylabel("频率 (Hz)", fontsize=14)
plt.colorbar(label='功率谱密度 (dB/Hz)')
plt.tight_layout()
plt.show()

print("Visualize time-varying PSD with colormap at how2matplotlib.com")

这个示例使用signal.spectrogram()函数计算短时傅里叶变换，然后使用plt.pcolormesh()函数绘制颜色图。颜色图的x轴表示时间，y轴表示频率，颜色深浅表示功率谱密度的大小。这种可视化方法特别适合分析频率随时间变化的信号。

8. 3D功率谱密度图

为了更直观地展示时变功率谱密度，我们可以创建3D功率谱密度图：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from mpl_toolkits.mplot3d import Axes3D

# 生成时变信号
t = np.linspace(0, 10, 1000)
f1, f2 = 5, 10
signal = np.sin(2 * np.pi * f1 * t) + np.sin(2 * np.pi * f2 * t * t / 20)

# 计算短时傅里叶变换
f, t, Sxx = signal.spectrogram(signal, fs=100, nperseg=64, noverlap=32)

# 创建3D图
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制3D功率谱密度图
T, F = np.meshgrid(t, f)
surf = ax.plot_surface(T, F, 10 * np.log10(Sxx), cmap='viridis')

ax.set_title("3D功率谱密度图 - how2matplotlib.com", fontsize=16)
ax.set_xlabel("时间 (秒)", fontsize=14)
ax.set_ylabel("频率 (Hz)", fontsize=14)
ax.set_zlabel("功率谱密度 (dB/Hz)", fontsize=14)

fig.colorbar(surf, shrink=0.5, aspect=5)
plt.tight_layout()
plt.show()

print("Create 3D PSD plots with Matplotlib at how2matplotlib.com")

这个示例使用Matplotlib的3D绘图功能创建了一个3D功率谱密度图。x轴表示时间，y轴表示频率，z轴表示功率谱密度。这种3D可视化方法可以更清晰地展示信号的时频特性。

9. 使用窗函数改善功率谱密度估计

在计算功率谱密度时，使用适当的窗函数可以改善估计的质量。Matplotlib和SciPy提供了多种窗函数供选择：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
freq1, freq2 = 10, 20
signal = np.sin(2 * np.pi * freq1 * t) + 0.5 * np.sin(2 * np.pi * freq2 * t)
noise = np.random.normal(0, 0.1, len(t))
signal_with_noise = signal + noise

# 定义不同的窗函数
windows = ['boxcar', 'hanning', 'hamming', 'blackman']

# 创建子图
fig, axs = plt.subplots(2, 2, figsize=(12, 10))
axs = axs.ravel()

for i, window in enumerate(windows):
    f, Pxx = signal.welch(signal_with_noise, fs=1000, nperseg=256, window=window)
    axs[i].semilogy(f, Pxx)
    axs[i].set_title(f"{window.capitalize()}窗 - how2matplotlib.com", fontsize=12)
    axs[i].set_xlabel("频率 (Hz)", fontsize=10)
    axs[i].set_ylabel("功率谱密度 (V^2/Hz)", fontsize=10)
    axs[i].set_xlim(0, 50)
    axs[i].grid(True)

plt.tight_layout()
plt.show()

print("Compare different window functions for PSD estimation at how2matplotlib.com")

这个示例比较了四种不同窗函数（矩形窗、汉宁窗、汉明窗和布莱克曼窗）对功率谱密度估计的影响。通过比较不同窗函数的结果，我们可以选择最适合特定信号分析需求的窗函数。

10. 分析实际数据的功率谱密度

在实际应用中，我们经常需要分析来自真实世界的数据。以下是一个分析音频信号功率谱密度的示例：

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import wavfile
from scipy import signal

# 读取音频文件（请确保文件路径正确）
sample_rate, audio_data = wavfile.read('example_audio.wav')

# 如果音频是立体声，只取一个声道
if len(audio_data.shape) > 1:
    audio_data = audio_data[:, 0]

# 计算功率谱密度
f, Pxx = signal.welch(audio_data, fs=sample_rate, nperseg=1024)

# 绘制功率谱密度图
plt.figure(figsize=(12, 6))
plt.semilogy(f, Pxx)
plt.title("音频信号的功率谱密度 - how2matplotlib.com", fontsize=16)
plt.xlabel("频率 (Hz)", fontsize=14)
plt.ylabel("功率谱密度 (V^2/Hz)", fontsize=14)
plt.xlim(0, sample_rate / 2)  # 限制到奈奎斯特频率
plt.grid(True)
plt.tight_layout()
plt.show()

print("Analyze real-world audio data with PSD plots at how2matplotlib.com")

这个示例演示了如何读取WAV音频文件，计算其功率谱密度，并使用Matplotlib绘制结果。通过分析功率谱密度图，我们可以了解音频信号中主要频率成分的分布情况。

11. 使用功率谱密度进行信号去噪

功率谱密度分析可以用于信号去噪。通过识别噪声的频率特征，我们可以设计适当的滤波器来减少噪声：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成含噪声的信号
t = np.linspace(0, 1, 1000, endpoint=False)
freq = 10
clean_signal = np.sin(2 * np.pi * freq * t)
noise = np.random.normal(0, 0.5, len(t))
noisy_signal = clean_signal + noise

# 计算原始信号的功率谱密度
f, Pxx_noisy = signal.welch(noisy_signal, fs=1000, nperseg=256)

# 设计低通滤波器
b, a = signal.butter(4, 20, 'low', fs=1000)

# 应用滤波器
filtered_signal = signal.filtfilt(b, a, noisy_signal)

# 计算滤波后信号的功率谱密度
f, Pxx_filtered = signal.welch(filtered_signal, fs=1000, nperseg=256)

# 绘图比较
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10))

ax1.plot(t, noisy_signal, label='含噪声信号')
ax1.plot(t, filtered_signal, label='滤波后信号')
ax1.set_title("时域信号比较 - how2matplotlib.com", fontsize=14)
ax1.set_xlabel("时间 (秒)", fontsize=12)
ax1.set_ylabel("振幅", fontsize=12)
ax1.legend()
ax1.grid(True)

ax2.semilogy(f, Pxx_noisy, label='含噪声信号')
ax2.semilogy(f, Pxx_filtered, label='滤波后信号')
ax2.set_title("功率谱密度比较 - how2matplotlib.com", fontsize=14)
ax2.set_xlabel("频率 (Hz)", fontsize=12)
ax2.set_ylabel("功率谱密度 (V^2/Hz)", fontsize=12)
ax2.set_xlim(0, 50)
ax2.legend()
ax2.grid(True)

plt.tight_layout()
plt.show()

print("Learn signal denoising techniques with PSD analysis at how2matplotlib.com")

Output:

使用Matplotlib绘制功率谱密度图：Python数据可视化指南

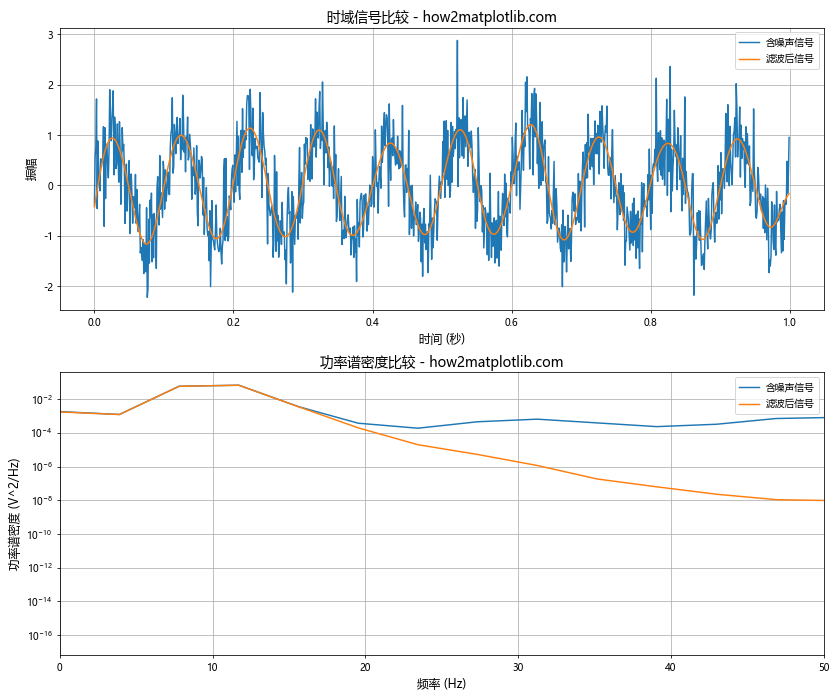
这个示例展示了如何使用功率谱密度分析来设计和应用低通滤波器，从而减少信号中的高频噪声。通过比较滤波前后的时域信号和功率谱密度，我们可以直观地看到滤波的效果。

12. 使用功率谱密度进行信号特征提取

功率谱密度分析还可以用于信号特征提取，例如识别信号中的主要频率成分：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成包含多个频率成分的信号
t = np.linspace(0, 1, 1000, endpoint=False)
freq1, freq2, freq3 = 10, 20, 30
signal = np.sin(2 * np.pi * freq1 * t) + 0.5 * np.sin(2 * np.pi * freq2 * t) + 0.3 * np.sin(2 * np.pi * freq3 * t)
noise = np.random.normal(0, 0.1, len(t))
signal_with_noise = signal + noise

# 计算功率谱密度
f, Pxx = signal.welch(signal_with_noise, fs=1000, nperseg=256)

# 找出功率谱密度的峰值
peaks, _ = signal.find_peaks(Pxx, height=0.01)
peak_freqs = f[peaks]
peak_psd = Pxx[peaks]

# 绘制功率谱密度图和识别出的峰值
plt.figure(figsize=(12, 6))
plt.semilogy(f, Pxx)
plt.plot(peak_freqs, peak_psd, 'ro')
for i, freq in enumerate(peak_freqs):
    plt.annotate(f'{freq:.1f} Hz', (freq, peak_psd[i]), xytext=(5, 5), 
                 textcoords='offset points')

plt.title("信号特征提取：识别主要频率成分 - how2matplotlib.com", fontsize=16)
plt.xlabel("频率 (Hz)", fontsize=14)
plt.ylabel("功率谱密度 (V^2/Hz)", fontsize=14)
plt.xlim(0, 50)
plt.grid(True)
plt.tight_layout()
plt.show()

print("Extract signal features using PSD analysis at how2matplotlib.com")

这个示例展示了如何使用功率谱密度分析来识别信号中的主要频率成分。通过找出功率谱密度曲线的峰值，我们可以确定信号中最显著的频率。这种技术在信号分类、故障诊断等领域有广泛应用。

总结

本文详细介绍了如何使用Matplotlib绘制功率谱密度图，并探讨了功率谱密度分析在信号处理中的多种应用。我们学习了以下关键内容：

  1. 功率谱密度的基本概念和意义
  2. 使用Matplotlib和SciPy绘制功率谱密度图的多种方法
  3. 自定义功率谱密度图的样式和布局
  4. 比较多个信号的功率谱密度
  5. 使用子图同时展示时域和频域分析结果
  6. 创建时变功率谱密度的颜色图和3D图
  7. 使用不同窗函数改善功率谱密度估计
  8. 分析实际音频数据的功率谱密度
  9. 利用功率谱密度分析进行信号去噪
  10. 使用功率谱密度进行信号特征提取

通过这些示例和技术，我们可以更好地理解和应用功率谱密度分析，从而在信号处理、数据分析和系统识别等领域获得更深入的洞察。

在实际应用中，功率谱密度分析可以帮助我们：

  • 识别信号中的主要频率成分
  • 检测周期性模式和隐藏的周期性
  • 评估噪声水平和信噪比
  • 设计适当的滤波器进行信号处理
  • 比较不同信号源的频率特性
  • 监测系统性能和故障诊断

为了进一步提高功率谱密度分析的效果，可以考虑以下建议：

  1. 选择合适的窗函数：不同的窗函数会影响频谱泄漏和分辨率，根据具体应用选择合适的窗函数很重要。

  2. 调整分段长度：在使用Welch方法时，调整分段长度可以平衡频率分辨率和统计可靠性。

  3. 使用对数刻度：对于宽动态范围的信号，使用对数刻度可以更好地显示低功率频率成分。

  4. 结合其他分析方法：将功率谱密度分析与时频分析、相位分析等方法结合，可以获得更全面的信号特征。

  5. 考虑信号的非平稳性：对于非平稳信号，考虑使用短时傅里叶变换或小波变换等时变分析方法。

  6. 注意采样率和频率分辨率：确保采样率足够高以捕获感兴趣的频率范围，并选择适当的FFT长度以获得所需的频率分辨率。

  7. 处理有限长度数据：对于有限长度的数据，考虑使用零填充或其他技术来改善频率分辨率。

  8. 验证结果：通过模拟数据或已知特性的信号来验证你的分析方法和结果的准确性。

最后，持续学习和实践是掌握功率谱密度分析的关键。随着技术的发展，新的算法和工具不断涌现，保持对最新进展的关注将有助于你在这个领域保持竞争力。

扩展阅读

为了深入了解功率谱密度分析和相关技术，以下是一些推荐的扩展阅读材料：

  1. “The Scientist and Engineer’s Guide to Digital Signal Processing” by Steven W. Smith
  2. “Spectral Analysis and Time Series” by M.B. Priestley
  3. “Digital Spectral Analysis with Applications” by S. Lawrence Marple Jr.
  4. “Practical Time Series Analysis” by Aileen Nielsen
  5. “Python for Signal Processing” by José Unpingco

这些资源可以帮助你更深入地理解信号处理的理论基础和实际应用，从而更好地运用功率谱密度分析技术。

结语

功率谱密度分析是信号处理中的一个强大工具，它能够揭示信号的频率特性，帮助我们更好地理解和处理各种类型的数据。通过本文的学习，你已经掌握了使用Matplotlib绘制功率谱密度图的多种方法，以及如何应用这些技术来解决实际问题。

记住，数据可视化不仅仅是创建图表，更重要的是通过视觉化手段来传达信息和洞察。在使用功率谱密度图时，始终考虑你的目标受众和你想要传达的关键信息。选择适当的图表类型、颜色方案和标注，可以大大提高你的分析结果的可读性和影响力。

继续探索和实践，你会发现功率谱密度分析在各个领域都有广泛的应用，从音频处理到地震数据分析，从生物医学信号处理到金融时间序列分析。掌握这项技能将为你的数据分析工具箱增添一个强大的武器。

Camera课程

Camera API2 教程

API2 教程
Camera 性能教程

Perf 教程
Camera Native Framework 教程

Native FW 教程
Camera QCOM ISP 教程

ISP 教程
Camera QCOM Sensor 教程

Sensor 教程

Python教程

Python 教程

Python 教程
NumPy 教程

NumPy 教程
Django 教程

Django 教程

Java教程

Java 教程

Java 教程

Web教程

JavaScript 教程

JavaScript 教程
jQuery 教程

jQuery 教程
CSS 教程

CSS 教程
PHP 教程

PHP 教程
Laravel 教程

Laravel 教程
TypeScript 教程

TypeScript 教程
WordPress 教程

WordPress 教程

数据库教程

SQL 教程

SQL 教程
SQLite 教程

SQLite 教程
MySQL 教程

MySQL 教程
PL/SQL 教程

PL/SQL 教程
MongoDB 教程

MongoDB 教程

图形图像教程

OpenCV 教程

OpenCV 教程

办公软件教程

Excel 教程

Excel 教程

Linux教程

Linux命令全集

Linux命令全集
Linux内核API

Linux内核API
LVGL 教程

LVGL 教程

计算机教程

操作系统 教程

操作系统 教程
计算机网络 教程

计算机网络 教程
C语言 教程

C语言 教程
C++ 教程

C++ 教程
Swift 教程

Swift 教程

大数据教程

Hadoop 教程

Hadoop 教程
Spark 教程

Spark 教程
Scala 教程

Scala 教程

开发工具教程

Git 教程

Git 教程
Jenkins 教程

Jenkins 教程
ChatGPT 教程

ChatGPT 教程
IntelliJ 教程

IntelliJ 教程