使用Matplotlib在Python中绘制相位谱:全面指南
参考:Plot the phase spectrum in Python using Matplotlib
相位谱是信号处理和频域分析中的重要工具,它可以揭示信号中不同频率分量的相位信息。在Python中,我们可以利用强大的Matplotlib库来绘制相位谱,从而直观地展示信号的相位特性。本文将详细介绍如何使用Matplotlib在Python中绘制相位谱,包括基本概念、数据准备、绘图技巧以及高级定制方法。
1. 相位谱的基本概念
在开始绘制相位谱之前,我们需要理解一些基本概念:
1.1 什么是相位谱?
相位谱是信号在频域中各个频率分量的相位角度的图形表示。它与幅度谱一起构成了信号的完整频域表示。相位谱可以揭示信号中不同频率成分之间的相对时间关系或相位差异。
1.2 为什么相位谱重要?
相位谱在许多应用中都很重要,例如:
– 音频处理:分析声音信号的谐波结构
– 图像处理:研究图像的空间频率特性
– 通信系统:评估信号传输中的相位失真
– 地震学:分析地震波的传播特性
1.3 如何计算相位谱?
相位谱通常通过以下步骤计算:
1. 对信号进行傅里叶变换,得到复数形式的频域表示
2. 计算每个频率分量的相位角度(通常使用arctan2函数)
3. 将相位角度映射到[-π, π]或[0, 2π]区间
2. 使用Matplotlib绘制基本相位谱
让我们从一个简单的例子开始,展示如何使用Matplotlib绘制基本的相位谱。
import numpy as np
import matplotlib.pyplot as plt
# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 20 * t)
# 计算FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# 计算相位谱
phase_spectrum = np.angle(fft_result)
# 绘制相位谱
plt.figure(figsize=(10, 6))
plt.plot(frequencies[:len(frequencies)//2], phase_spectrum[:len(frequencies)//2])
plt.title('Phase Spectrum - how2matplotlib.com')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (radians)')
plt.grid(True)
plt.show()
Output:
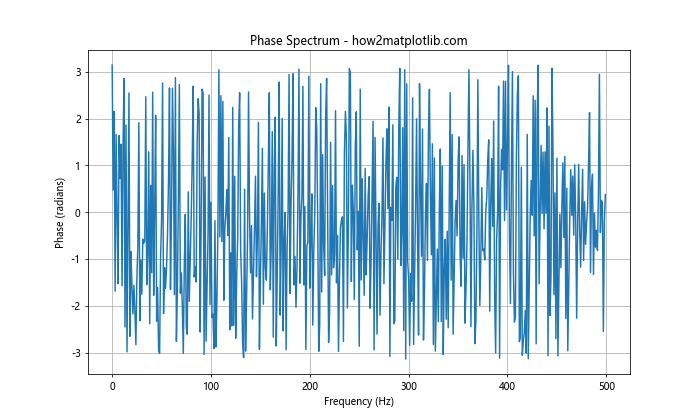
在这个例子中,我们首先生成了一个包含两个正弦分量的示例信号。然后,我们使用NumPy的FFT函数计算信号的傅里叶变换,并使用np.angle()函数计算相位角度。最后,我们使用Matplotlib的plot()函数绘制相位谱。
3. 改进相位谱的可视化
基本的相位谱图可能不够直观,我们可以通过一些技巧来改进其可视化效果。
3.1 使用散点图
散点图可以更清晰地显示离散频率点的相位值。
import numpy as np
import matplotlib.pyplot as plt
# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 20 * t)
# 计算FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# 计算相位谱
phase_spectrum = np.angle(fft_result)
# 绘制相位谱散点图
plt.figure(figsize=(10, 6))
plt.scatter(frequencies[:len(frequencies)//2], phase_spectrum[:len(frequencies)//2], alpha=0.5)
plt.title('Phase Spectrum (Scatter Plot) - how2matplotlib.com')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (radians)')
plt.grid(True)
plt.show()
Output:
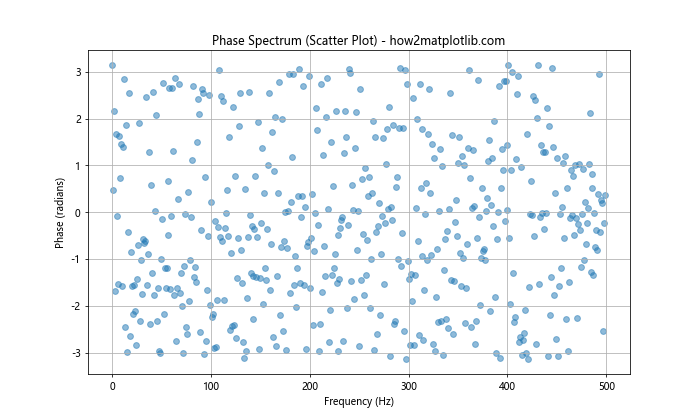
这个例子使用plt.scatter()函数替代了plt.plot(),从而创建了一个散点图。这种表示方式可以更清楚地显示每个频率点的相位值。
3.2 添加颜色映射
我们可以使用颜色映射来表示相位值的大小,这样可以增加图表的信息量。
import numpy as np
import matplotlib.pyplot as plt
# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 20 * t)
# 计算FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# 计算相位谱
phase_spectrum = np.angle(fft_result)
# 绘制带颜色映射的相位谱
plt.figure(figsize=(10, 6))
scatter = plt.scatter(frequencies[:len(frequencies)//2], phase_spectrum[:len(frequencies)//2],
c=phase_spectrum[:len(frequencies)//2], cmap='hsv', alpha=0.5)
plt.colorbar(scatter, label='Phase (radians)')
plt.title('Phase Spectrum with Color Mapping - how2matplotlib.com')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (radians)')
plt.grid(True)
plt.show()
Output:
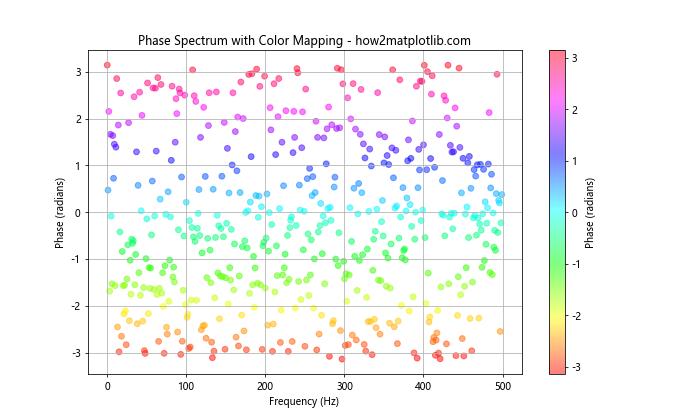
在这个例子中,我们使用plt.scatter()函数的c参数来设置点的颜色,并使用cmap参数指定颜色映射。plt.colorbar()函数添加了一个颜色条,显示相位值的范围。
4. 处理相位谱的不连续性
相位谱通常会在-π和π之间跳变,这可能导致图形看起来不连续。我们可以通过展开相位来解决这个问题。
import numpy as np
import matplotlib.pyplot as plt
# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 20 * t)
# 计算FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# 计算相位谱并展开
phase_spectrum = np.unwrap(np.angle(fft_result))
# 绘制展开后的相位谱
plt.figure(figsize=(10, 6))
plt.plot(frequencies[:len(frequencies)//2], phase_spectrum[:len(frequencies)//2])
plt.title('Unwrapped Phase Spectrum - how2matplotlib.com')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Unwrapped Phase (radians)')
plt.grid(True)
plt.show()
Output:
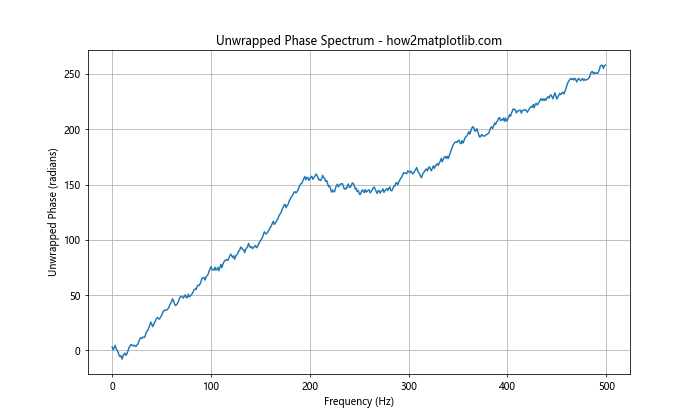
在这个例子中,我们使用np.unwrap()函数来展开相位谱。这个函数通过添加适当的2π倍数来消除相位的跳变,使得相位谱看起来更加连续。
5. 结合幅度谱和相位谱
有时候,同时查看幅度谱和相位谱会很有帮助。我们可以使用Matplotlib的子图功能来实现这一点。
import numpy as np
import matplotlib.pyplot as plt
# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 20 * t)
# 计算FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# 计算幅度谱和相位谱
magnitude_spectrum = np.abs(fft_result)
phase_spectrum = np.angle(fft_result)
# 创建子图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 10))
# 绘制幅度谱
ax1.plot(frequencies[:len(frequencies)//2], magnitude_spectrum[:len(frequencies)//2])
ax1.set_title('Magnitude Spectrum - how2matplotlib.com')
ax1.set_xlabel('Frequency (Hz)')
ax1.set_ylabel('Magnitude')
ax1.grid(True)
# 绘制相位谱
ax2.plot(frequencies[:len(frequencies)//2], phase_spectrum[:len(frequencies)//2])
ax2.set_title('Phase Spectrum - how2matplotlib.com')
ax2.set_xlabel('Frequency (Hz)')
ax2.set_ylabel('Phase (radians)')
ax2.grid(True)
plt.tight_layout()
plt.show()
Output:
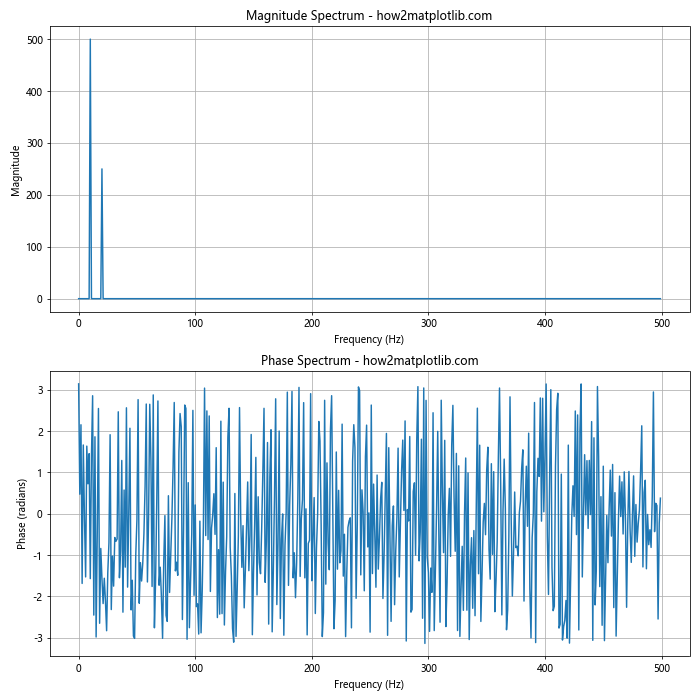
这个例子创建了两个子图,上面显示幅度谱,下面显示相位谱。这种表示方式可以让我们同时观察信号的幅度和相位特性。
6. 使用极坐标系表示相位谱
相位是角度量,因此使用极坐标系来表示相位谱有时会更加直观。
import numpy as np
import matplotlib.pyplot as plt
# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 20 * t)
# 计算FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# 计算相位谱
phase_spectrum = np.angle(fft_result)
# 创建极坐标图
fig, ax = plt.subplots(subplot_kw=dict(projection='polar'), figsize=(10, 10))
# 绘制相位谱
ax.scatter(phase_spectrum[:len(frequencies)//2], frequencies[:len(frequencies)//2], alpha=0.5)
ax.set_title('Phase Spectrum in Polar Coordinates - how2matplotlib.com')
ax.set_theta_zero_location('N')
ax.set_theta_direction(-1)
ax.set_thetamin(-180)
ax.set_thetamax(180)
ax.set_ylabel('Frequency (Hz)')
ax.set_ylim(0, max(frequencies[:len(frequencies)//2]))
plt.show()
Output:
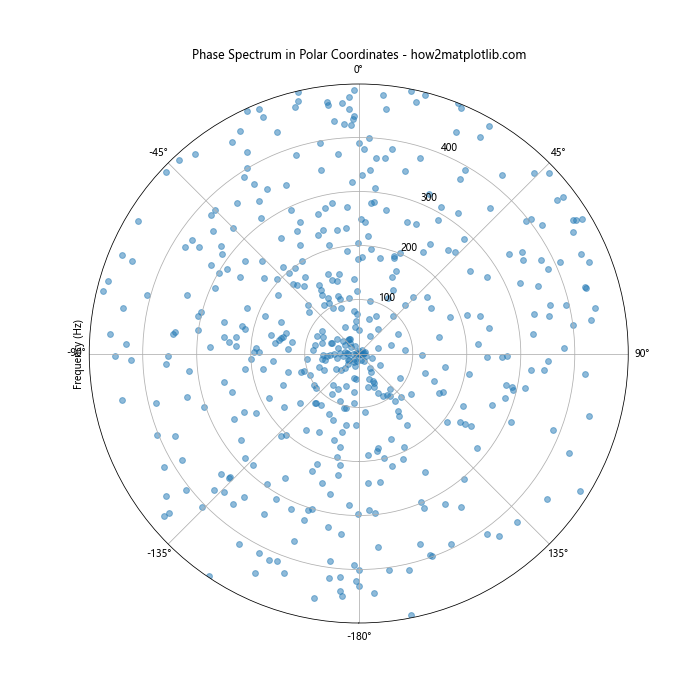
在这个例子中,我们使用极坐标系来表示相位谱。相位角度被映射到圆周上,而频率被映射到半径上。这种表示方式可以直观地显示不同频率分量的相位关系。
7. 处理复杂信号的相位谱
对于更复杂的信号,相位谱可能会变得难以解释。我们可以使用一些技巧来改善可视化效果。
7.1 使用对数频率轴
对于宽频带信号,使用对数频率轴可以更好地显示低频和高频部分的相位信息。
import numpy as np
import matplotlib.pyplot as plt
# 生成复杂信号
t = np.linspace(0, 1, 10000, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 100 * t) + 0.2 * np.sin(2 * np.pi * 1000 * t)
# 计算FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# 计算相位谱
phase_spectrum = np.angle(fft_result)
# 绘制使用对数频率轴的相位谱
plt.figure(figsize=(10, 6))
plt.semilogx(frequencies[:len(frequencies)//2], phase_spectrum[:len(frequencies)//2])
plt.title('Phase Spectrum with Log Frequency Axis - how2matplotlib.com')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (radians)')
plt.grid(True)
plt.show()
Output:
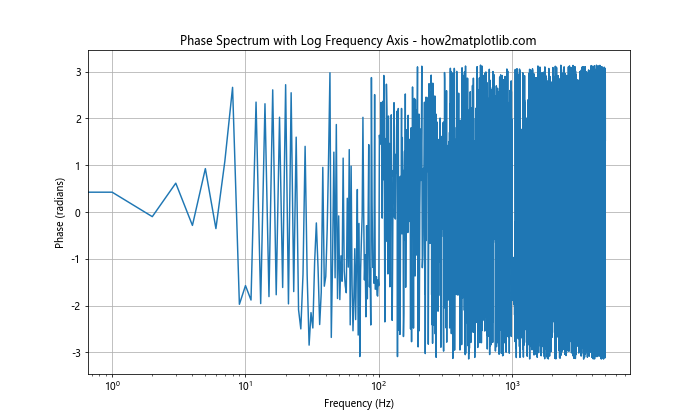
在这个例子中,我们使用plt.semilogx()函数来创建一个x轴为对数刻度的图表。这对于显示宽频带信号的相位谱特别有用。
7.2 相位谱的平滑处理
对于噪声信号,相位谱可能会显得杂乱。我们可以使用平滑技术来改善可视化效果。
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import savgol_filter
# 生成带噪声的信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 20 * t) + 0.1 * np.random.randn(len(t))
# 计算FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# 计算相位谱
phase_spectrum = np.angle(fft_result)
# 平滑处理
smoothed_phase = savgol_filter(phase_spectrum, window_length=51, polyorder=3)
# 绘制原始和平滑后的相位谱
plt.figure(figsize=(10, 6))
plt.plot(frequencies[:len(frequencies)//2], phase_spectrum[:len(frequencies)//2], alpha=0.5, label='Original')
plt.plot(frequencies[:len(frequencies)//2], smoothed_phase[:len(frequencies)//2], label='Smoothed')
plt.title('Original vs Smoothed Phase Spectrum - how2matplotlib.com')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (radians)')
plt.legend()
plt.grid(True)
plt.show()
Output:
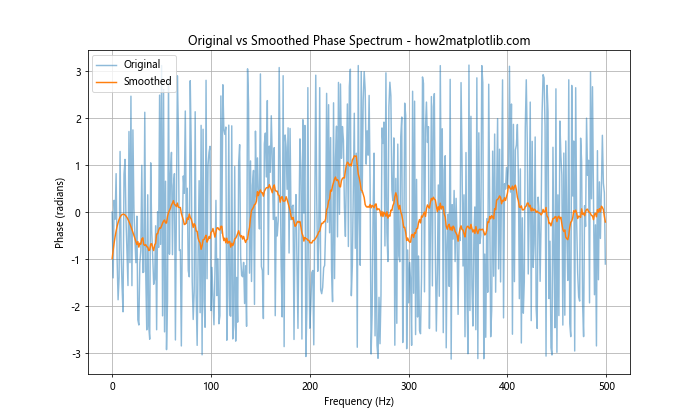
在这个例子中,我们使用SciPy的savgol_filter函数对相位谱进行平滑处理。这可以帮助减少噪声的影响,使相位谱的主要特征更加明显。
8. 相位谱的高级应用
相位谱在信号处理中有许多高级应用。让我们探讨几个例子。
8.1 群延迟的计算和可视化
群延迟是相位谱对频率的负导数,它表示信号中不同频率分量的相对延迟。
import numpy as np
import matplotlib.pyplot as plt
# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 20 * t)
# 计算FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# 计算相位谱
phase_spectrum = np.unwrap(np.angle(fft_result))
# 计算群延迟
group_delay = -np.diff(phase_spectrum) / np.diff(frequencies)
# 绘制群延迟
plt.figure(figsize=(10, 6))
plt.plot(frequencies[1:len(frequencies)//2], group_delay[:len(frequencies)//2-1])
plt.title('Group Delay - how2matplotlib.com')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Group Delay (seconds)')
plt.grid(True)
plt.show()
Output:
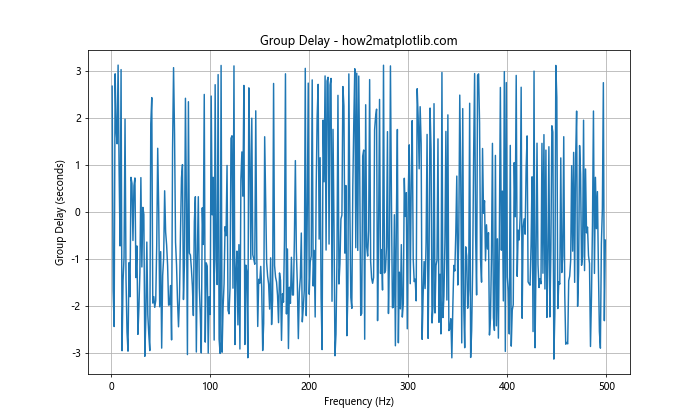
这个例子展示了如何计算和绘制群延迟。群延迟可以揭示信号中不同频率分量的时间延迟特性。
8.2 相位谱的时间-频率分析
我们可以使用短时傅里叶变换(STFT)来分析信号相位随时间的变化。
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import stft
# 生成时变信号
t = np.linspace(0, 10, 10000, endpoint=False)
signal = np.sin(2 * np.pi * (1 + t/10) * t)
# 计算STFT
f, t, Zxx = stft(signal, fs=1000, nperseg=1000)
# 提取相位信息
phase = np.angle(Zxx)
# 绘制相位谱图
plt.figure(figsize=(10, 6))
plt.pcolormesh(t, f, phase, shading='gouraud', cmap='hsv')
plt.title('Phase Spectrogram - how2matplotlib.com')
plt.xlabel('Time (s)')
plt.ylabel('Frequency (Hz)')
plt.colorbar(label='Phase (radians)')
plt.show()
Output:
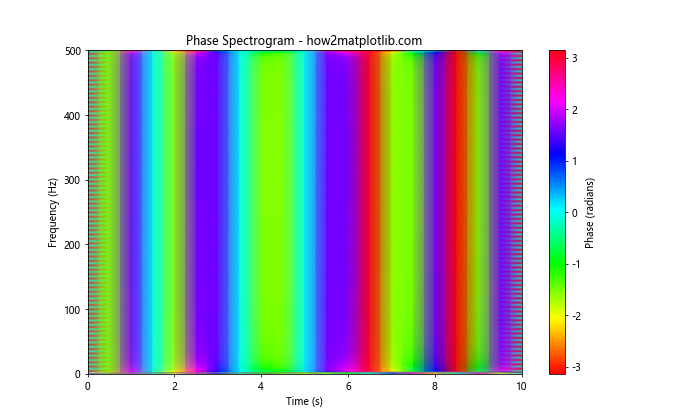
这个例子使用scipy.signal.stft函数计算短时傅里叶变换,然后绘制相位谱图。这种表示方法可以显示信号相位随时间和频率的变化。
9. 自定义相位谱的外观
Matplotlib提供了丰富的选项来自定义图表的外观。让我们探讨一些常用的自定义技巧。
9.1 设置颜色和样式
我们可以通过设置线条的颜色、样式和宽度来改变相位谱的外观。
import numpy as np
import matplotlib.pyplot as plt
# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 20 * t)
# 计算FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# 计算相位谱
phase_spectrum = np.angle(fft_result)
# 绘制自定义样式的相位谱
plt.figure(figsize=(10, 6))
plt.plot(frequencies[:len(frequencies)//2], phase_spectrum[:len(frequencies)//2],
color='purple', linestyle='--', linewidth=2)
plt.title('Customized Phase Spectrum - how2matplotlib.com', fontsize=16)
plt.xlabel('Frequency (Hz)', fontsize=12)
plt.ylabel('Phase (radians)', fontsize=12)
plt.grid(True, linestyle=':')
plt.show()
Output:
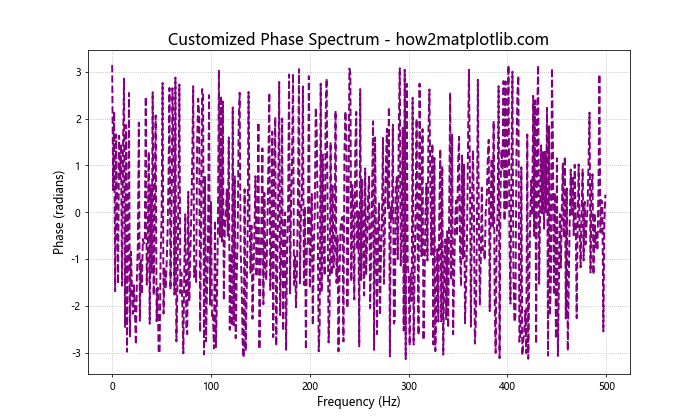
在这个例子中,我们设置了线条的颜色、样式和宽度,并自定义了标题和轴标签的字体大小。
9.2 添加注释和标记
我们可以在相位谱图上添加注释和标记来突出重要特征。
import numpy as np
import matplotlib.pyplot as plt
# 生成示例信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 20 * t)
# 计算FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# 计算相位谱
phase_spectrum = np.angle(fft_result)
# 绘制相位谱并添加注释
plt.figure(figsize=(10, 6))
plt.plot(frequencies[:len(frequencies)//2], phase_spectrum[:len(frequencies)//2])
plt.title('Phase Spectrum with Annotations - how2matplotlib.com')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (radians)')
# 添加注释
plt.annotate('Peak at 10 Hz', xy=(10, phase_spectrum[np.argmin(np.abs(frequencies-10))]),
xytext=(15, 1), arrowprops=dict(facecolor='black', shrink=0.05))
# 添加标记
plt.axvline(x=20, color='r', linestyle='--', label='20 Hz component')
plt.legend()
plt.grid(True)
plt.show()
Output:
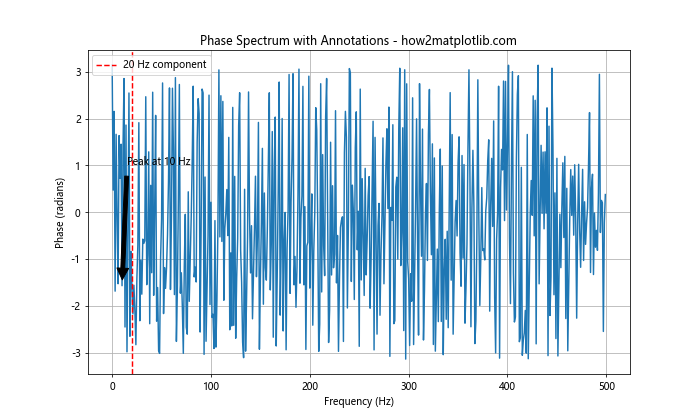
这个例子展示了如何在相位谱图上添加文本注释和垂直线标记。这些元素可以帮助突出图中的重要特征。
10. 处理实际数据的相位谱
在实际应用中,我们经常需要处理来自真实世界的数据。让我们看一个处理音频信号相位谱的例子。
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import wavfile
# 读取音频文件
sample_rate, audio_data = wavfile.read('example_audio.wav') # 请替换为实际的音频文件路径
# 如果是立体声,只取一个声道
if audio_data.ndim > 1:
audio_data = audio_data[:, 0]
# 计算FFT
fft_result = np.fft.fft(audio_data)
frequencies = np.fft.fftfreq(len(audio_data), 1/sample_rate)
# 计算相位谱
phase_spectrum = np.angle(fft_result)
# 绘制相位谱
plt.figure(figsize=(12, 6))
plt.plot(frequencies[:len(frequencies)//2], phase_spectrum[:len(frequencies)//2])
plt.title('Phase Spectrum of Audio Signal - how2matplotlib.com')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (radians)')
plt.xlim(0, 5000) # 限制频率范围以便更好地观察
plt.grid(True)
plt.show()
这个例子展示了如何读取音频文件,计算其相位谱,并绘制结果。请注意,您需要替换 ‘example_audio.wav’ 为实际的音频文件路径。
11. 相位谱的交互式可视化
Matplotlib还支持创建交互式图表,这对于探索复杂的相位谱数据特别有用。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider
# 生成初始信号
t = np.linspace(0, 1, 1000, endpoint=False)
initial_freq = 10
signal = np.sin(2 * np.pi * initial_freq * t)
# 计算初始FFT
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
phase_spectrum = np.angle(fft_result)
# 创建图形和轴
fig, ax = plt.subplots(figsize=(10, 8))
plt.subplots_adjust(bottom=0.25)
# 绘制初始相位谱
line, = ax.plot(frequencies[:len(frequencies)//2], phase_spectrum[:len(frequencies)//2])
ax.set_title('Interactive Phase Spectrum - how2matplotlib.com')
ax.set_xlabel('Frequency (Hz)')
ax.set_ylabel('Phase (radians)')
ax.grid(True)
# 创建滑块
ax_freq = plt.axes([0.2, 0.1, 0.6, 0.03])
freq_slider = Slider(ax_freq, 'Frequency', 1, 50, valinit=initial_freq)
# 更新函数
def update(val):
freq = freq_slider.val
signal = np.sin(2 * np.pi * freq * t)
fft_result = np.fft.fft(signal)
phase_spectrum = np.angle(fft_result)
line.set_ydata(phase_spectrum[:len(frequencies)//2])
fig.canvas.draw_idle()
# 连接滑块到更新函数
freq_slider.on_changed(update)
plt.show()
Output:
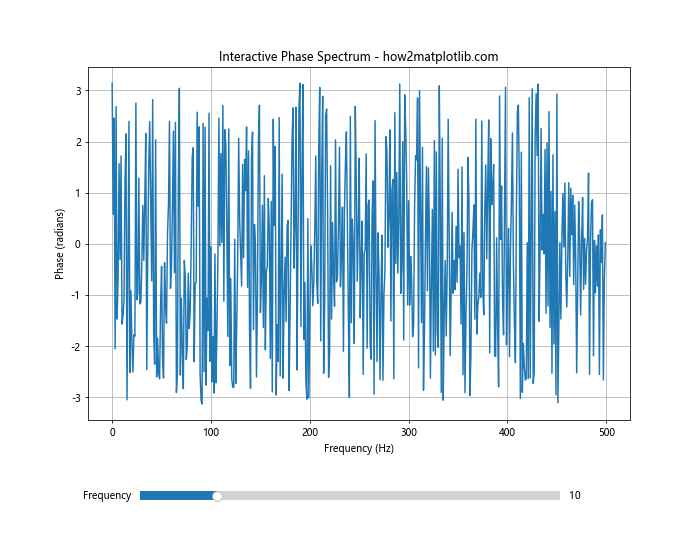
这个例子创建了一个交互式的相位谱图,用户可以通过滑块来调整信号的频率,并实时观察相位谱的变化。
12. 结论
通过本文,我们详细探讨了如何使用Matplotlib在Python中绘制相位谱。我们从基本概念开始,逐步深入到更复杂的技术和应用。我们学习了如何改进相位谱的可视化效果,处理复杂信号,以及自定义图表外观。我们还探讨了相位谱的高级应用,如群延迟的计算和时间-频率分析。
相位谱分析是信号处理中的重要工具,它可以揭示信号中隐藏的时间和频率特性。通过掌握这些技术,您将能够更深入地理解和分析各种类型的信号,从简单的正弦波到复杂的音频和图像数据。
记住,相位谱分析通常与幅度谱分析结合使用,以获得信号的完整频域表示。在实际应用中,您可能需要根据具体问题和数据特性来选择和调整这些技术。
继续探索和实践,您将发现Matplotlib是一个强大而灵活的工具,可以帮助您创建丰富的相位谱可视化,从而更好地理解和分析各种信号。
 极客笔记
极客笔记