Matplotlib热图插值技术详解

Matplotlib热图插值技术详解

参考：matplotlib heatmap interpolation

matplotlib heatmap interpolation

Matplotlib是Python中最流行的数据可视化库之一，它提供了强大的绘图功能，包括热图（heatmap）的绘制。热图是一种用颜色来表示数据大小的二维图形，常用于展示矩阵数据或者二维数据分布。在绘制热图时，插值（interpolation）技术扮演着重要的角色，它可以帮助我们在有限的数据点之间创建平滑的过渡，从而生成更加美观和易于理解的可视化效果。

本文将深入探讨Matplotlib中热图的插值技术，包括其原理、常用方法以及实际应用。我们将通过大量的示例代码来展示如何使用不同的插值方法，以及如何根据具体需求选择合适的插值技术。

1. 热图基础

热图是一种将矩阵数据可视化的方法，其中每个单元格的颜色代表了相应的数值大小。在Matplotlib中，我们主要使用imshow()函数来创建热图。

让我们从一个简单的热图示例开始：

import numpy as np
import matplotlib.pyplot as plt

# 创建一个简单的数据矩阵
data = np.array([
    [1, 2, 3, 4],
    [5, 6, 7, 8],
    [9, 10, 11, 12],
    [13, 14, 15, 16]
])

# 创建热图
plt.figure(figsize=(8, 6))
plt.imshow(data, cmap='viridis')
plt.colorbar(label='Value')
plt.title('Simple Heatmap - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
print("热图已生成，请查看图像窗口。")
plt.show()

Output:

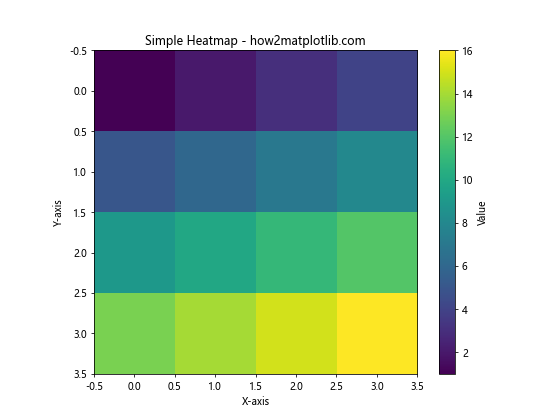
在这个例子中，我们创建了一个4×4的数据矩阵，并使用imshow()函数将其可视化为热图。cmap='viridis'参数指定了颜色映射方案，colorbar()函数添加了一个颜色条来显示数值和颜色的对应关系。

2. 插值的概念和重要性

插值是在已知数据点之间估算未知数据点值的过程。在热图中，插值可以帮助我们创建更加平滑和连续的视觉效果，特别是当原始数据分辨率较低时。

Matplotlib提供了多种插值方法，可以通过imshow()函数的interpolation参数来指定。默认情况下，interpolation的值为'nearest'，这意味着不进行插值，每个数据点都表示为一个矩形像素。

让我们看一个对比示例，展示插值的效果：

import numpy as np
import matplotlib.pyplot as plt

# 创建一个低分辨率的数据矩阵
data = np.random.rand(5, 5)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

# 不使用插值
ax1.imshow(data, interpolation='nearest')
ax1.set_title('Without Interpolation - how2matplotlib.com')

# 使用双线性插值
ax2.imshow(data, interpolation='bilinear')
ax2.set_title('With Bilinear Interpolation - how2matplotlib.com')

for ax in (ax1, ax2):
    ax.set_xlabel('X-axis')
    ax.set_ylabel('Y-axis')

plt.tight_layout()
print("对比图已生成，请查看图像窗口。")
plt.show()

Output:

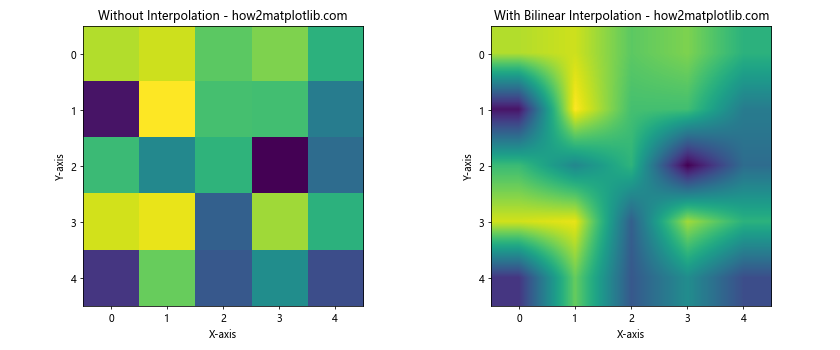
在这个例子中，我们创建了一个5×5的随机数据矩阵，并分别使用无插值和双线性插值方法绘制热图。可以看到，使用插值后的图像更加平滑，边界过渡更加自然。

3. Matplotlib中的插值方法

Matplotlib提供了多种插值方法，每种方法都有其特定的用途和效果。以下是一些常用的插值方法：

1. ‘nearest’：最近邻插值
2. ‘bilinear’：双线性插值
3. ‘bicubic’：双三次插值
4. ‘spline16’：16阶样条插值
5. ‘spline36’：36阶样条插值
6. ‘hanning’：Hanning窗口插值
7. ‘hamming’：Hamming窗口插值
8. ‘hermite’：Hermite样条插值
9. ‘kaiser’：Kaiser窗口插值
10. ‘quadric’：二次插值
11. ‘catrom’：Catmull-Rom样条插值
12. ‘gaussian’：高斯插值
13. ‘bessel’：Bessel插值
14. ‘mitchell’：Mitchell-Netravali插值
15. ‘sinc’：Sinc插值
16. ‘lanczos’：Lanczos插值

让我们通过一个示例来比较这些插值方法的效果：

import numpy as np
import matplotlib.pyplot as plt

# 创建一个低分辨率的数据矩阵
data = np.random.rand(5, 5)

interpolation_methods = [
    'nearest', 'bilinear', 'bicubic', 'spline16', 'spline36', 'hanning',
    'hamming', 'hermite', 'kaiser', 'quadric', 'catrom', 'gaussian',
    'bessel', 'mitchell', 'sinc', 'lanczos'
]

fig, axes = plt.subplots(4, 4, figsize=(20, 20))
axes = axes.flatten()

for ax, method in zip(axes, interpolation_methods):
    ax.imshow(data, interpolation=method)
    ax.set_title(f'{method} - how2matplotlib.com')
    ax.axis('off')

plt.tight_layout()
print("各种插值方法对比图已生成，请查看图像窗口。")
plt.show()

Output:

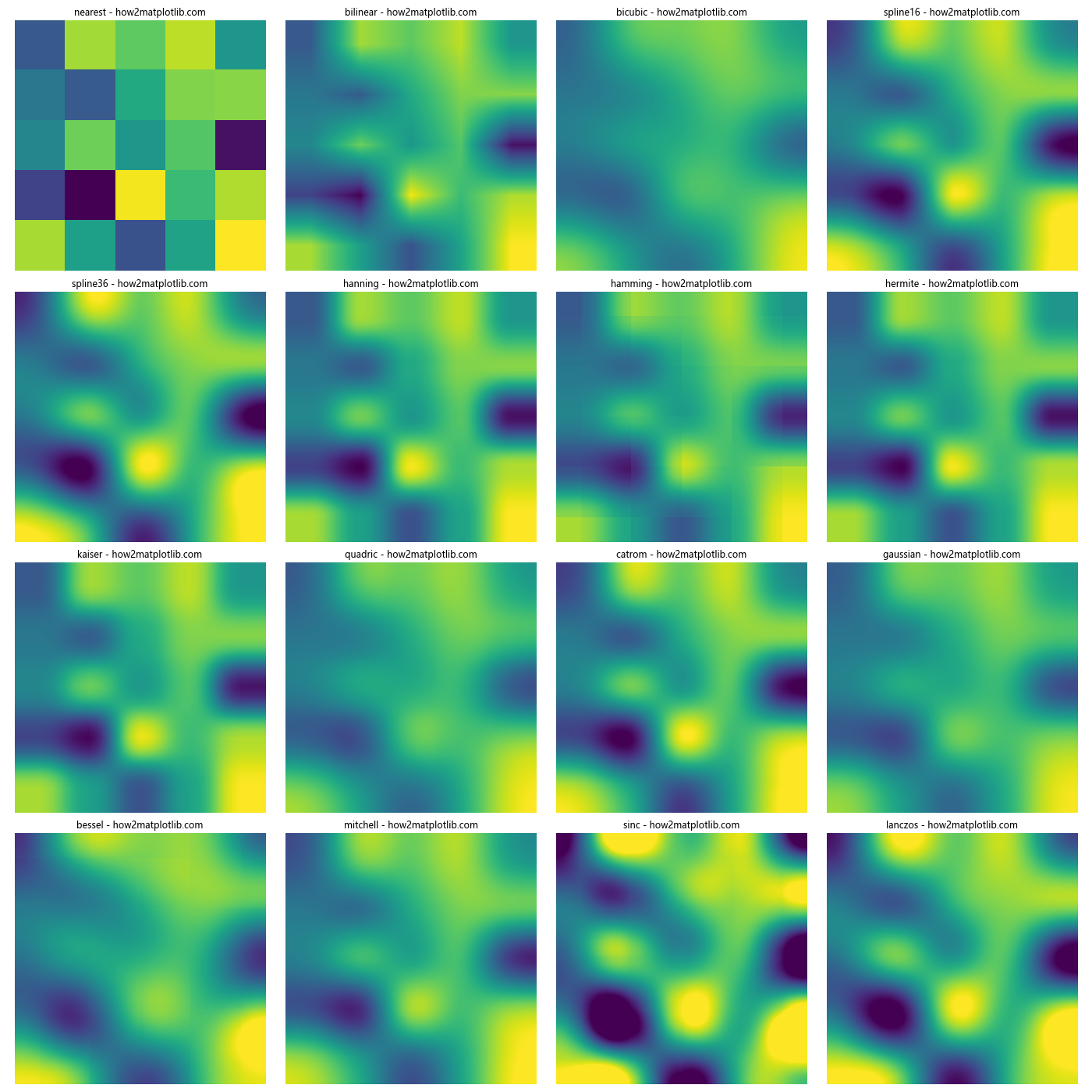
这个示例创建了一个4×4的网格，展示了16种不同插值方法的效果。通过比较这些图像，我们可以看到不同插值方法在平滑度、细节保留和边缘处理等方面的差异。

4. 选择合适的插值方法

选择合适的插值方法取决于多个因素，包括：

1. 数据的性质：是否需要保留锐利的边缘或平滑的过渡。
2. 计算效率：某些插值方法可能比其他方法更耗时。
3. 视觉效果：不同的插值方法可能会产生不同的视觉效果。
4. 数据分辨率：对于低分辨率数据，更高级的插值方法可能会产生更好的结果。

以下是一些常见场景的建议：

• 对于需要保留锐利边缘的数据（如分类数据），使用’nearest’插值。
• 对于需要平滑过渡的连续数据，可以使用’bilinear’或’bicubic’插值。
• 对于高质量图像输出，可以考虑使用’spline36’或’lanczos’插值。
• 对于实时渲染或大型数据集，可能需要权衡计算效率，选择较简单的插值方法如’bilinear’。

让我们通过一个示例来展示如何根据数据类型选择合适的插值方法：

import numpy as np
import matplotlib.pyplot as plt

# 创建分类数据
categorical_data = np.random.randint(0, 5, (10, 10))

# 创建连续数据
continuous_data = np.random.rand(10, 10)

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

# 分类数据 - 使用nearest插值
axes[0, 0].imshow(categorical_data, interpolation='nearest')
axes[0, 0].set_title('Categorical Data (nearest) - how2matplotlib.com')

# 分类数据 - 使用bilinear插值（不推荐）
axes[0, 1].imshow(categorical_data, interpolation='bilinear')
axes[0, 1].set_title('Categorical Data (bilinear) - how2matplotlib.com')

# 连续数据 - 使用nearest插值
axes[1, 0].imshow(continuous_data, interpolation='nearest')
axes[1, 0].set_title('Continuous Data (nearest) - how2matplotlib.com')

# 连续数据 - 使用bilinear插值
axes[1, 1].imshow(continuous_data, interpolation='bilinear')
axes[1, 1].set_title('Continuous Data (bilinear) - how2matplotlib.com')

for ax in axes.flatten():
    ax.set_xlabel('X-axis')
    ax.set_ylabel('Y-axis')

plt.tight_layout()
print("数据类型与插值方法对比图已生成，请查看图像窗口。")
plt.show()

Output:

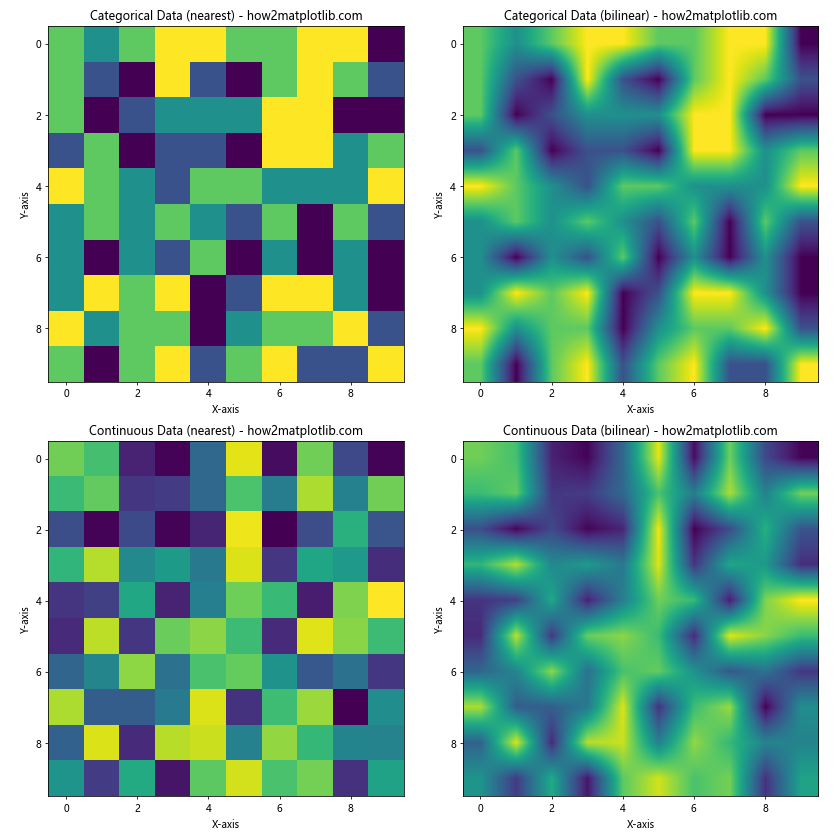
在这个例子中，我们分别为分类数据和连续数据使用了’nearest’和’bilinear’插值方法。可以看到，对于分类数据，’nearest’插值保留了清晰的边界，而’bilinear’插值则产生了不适当的中间值。对于连续数据，’bilinear’插值提供了更平滑的过渡效果。

5. 插值与图像缩放

插值不仅可以用于改善热图的视觉效果，还可以用于图像的缩放。当我们需要将热图调整到特定大小时，插值方法的选择会影响最终的图像质量。

让我们看一个示例，展示如何使用不同的插值方法来缩放热图：

import numpy as np
import matplotlib.pyplot as plt

# 创建一个小的数据矩阵
data = np.random.rand(5, 5)

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

interpolation_methods = ['nearest', 'bilinear', 'bicubic', 'lanczos']

for ax, method in zip(axes.flatten(), interpolation_methods):
    ax.imshow(data, interpolation=method, extent=[0, 10, 0, 10])
    ax.set_title(f'Scaled with {method} - how2matplotlib.com')
    ax.set_xlabel('X-axis')
    ax.set_ylabel('Y-axis')

plt.tight_layout()
print("缩放后的热图对比已生成，请查看图像窗口。")
plt.show()

Output:

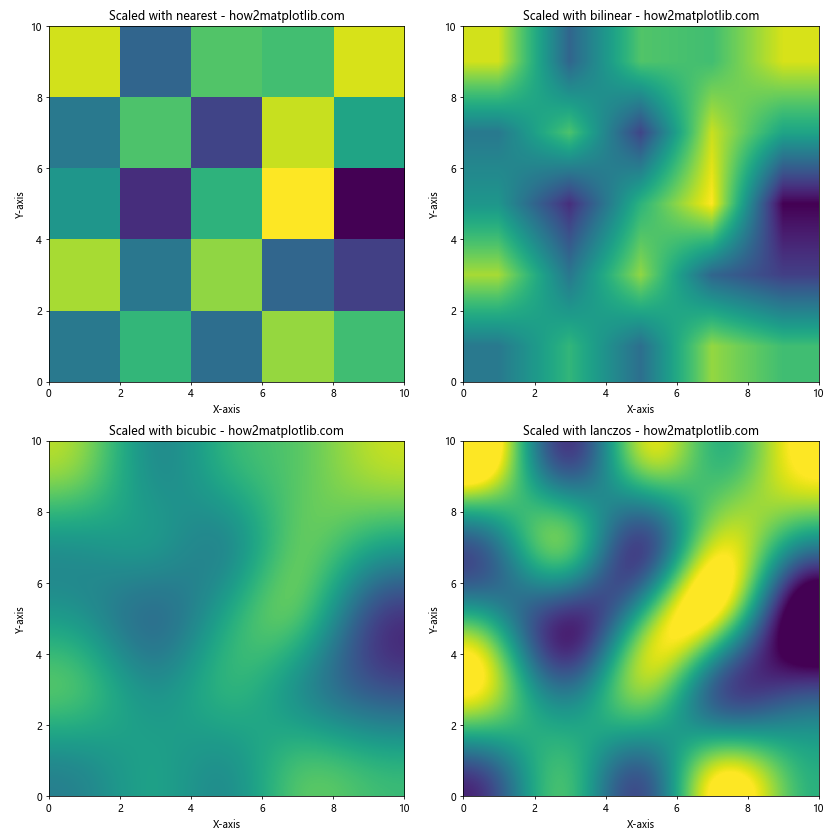
在这个例子中，我们创建了一个5×5的数据矩阵，但将其显示在一个10×10的范围内，这就需要进行插值来填充额外的像素。我们比较了四种不同的插值方法：’nearest’、’bilinear’、’bicubic’和’lanczos’。可以看到，不同的插值方法在处理图像缩放时会产生不同的效果。

6. 插值与颜色映射

插值不仅影响热图的形状和纹理，还会影响颜色的过渡。不同的颜色映射（colormap）与插值方法的组合可以产生不同的视觉效果。让我们探讨一下插值与颜色映射的关系：

import numpy as np
import matplotlib.pyplot as plt

# 创建数据
data = np.random.rand(10, 10)

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

colormaps = ['viridis', 'plasma', 'inferno', 'magma']
interpolations = ['nearest', 'bilinear']

for i, cmap in enumerate(colormaps):
    for j, interp in enumerate(interpolations):
        ax = axes[i // 2, i % 2]
        im = ax.imshow(data, cmap=cmap, interpolation=interp)
        ax.set_title(f'{cmap} with {interp} - how2matplotlib.com')
        plt.colorbar(im, ax=ax)

plt.tight_layout()
print("颜色映射与插值方法组合效果图已生成，请查看图像窗口。")
plt.show()

Output:

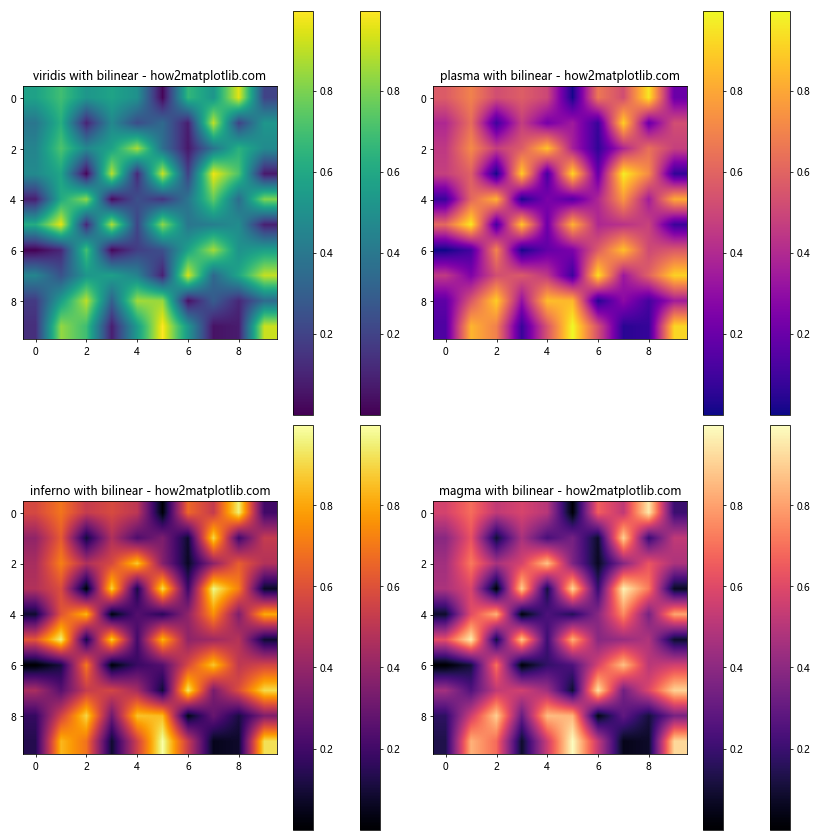
在这个例子中，我们展示了四种不同的颜色映射（viridis、plasma、inferno和magma）与两种插值方法（nearest和bilinear）的组合效果。可以看到，插值方法不仅影响了数据点之间的过渡，还影响了颜色的混合效果。

7. 插值与数据平滑

插值可以用于数据平滑，特别是当我们处理噪声数据时。然而，过度平滑可能会导致重要信息的丢失。让我们通过一个例子来探讨插值对数据平滑的影响：

import numpy as np
import matplotlib.pyplot as plt

# 创建带有噪声的数据
x = np.linspace(0, 10, 100)
y = np.linspace(0, 10, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)
noise = np.random.normal(0, 0.2, Z.shape)
Z_noisy = Z + noise

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

interpolation_methods = ['nearest', 'bilinear', 'bicubic', 'gaussian']

for ax, method in zip(axes.flatten(), interpolation_methods):
    im = ax.imshow(Z_noisy, interpolation=method, extent=[0, 10, 0, 10], cmap='viridis')
    ax.set_title(f'{method} interpolation - how2matplotlib.com')
    plt.colorbar(im, ax=ax)

plt.tight_layout()
print("不同插值方法对噪声数据的平滑效果图已生成，请查看图像窗口。")
plt.show()

Output:

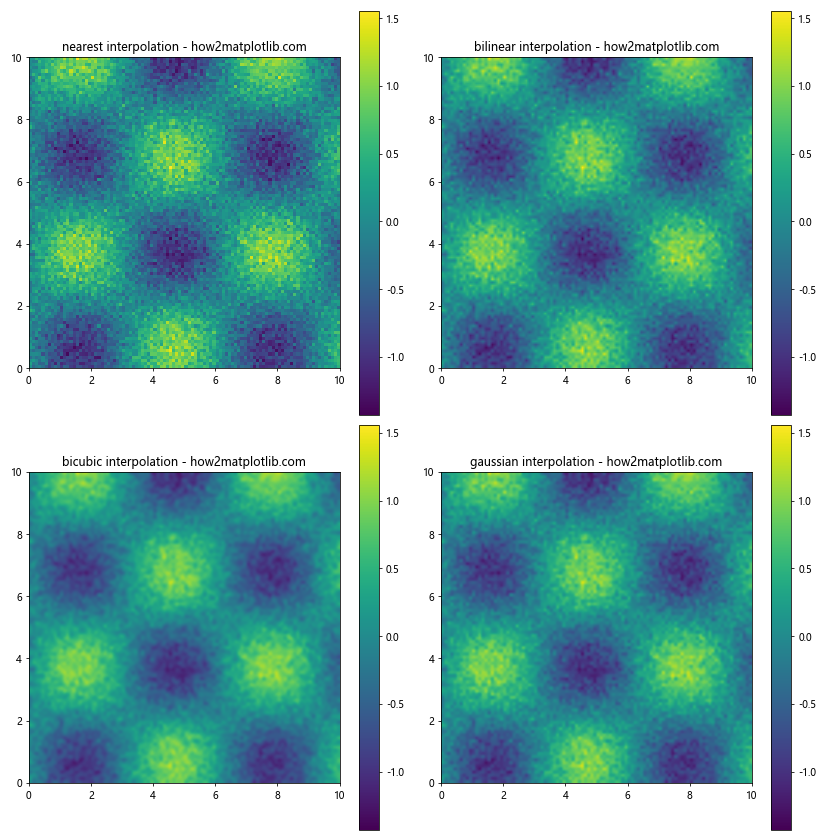
在这个例子中，我们创建了一个带有噪声的二维正弦波数据。然后，我们使用四种不同的插值方法（nearest、bilinear、bicubic和gaussian）来绘制热图。可以观察到，不同的插值方法对噪声数据的平滑效果不同：

• ‘nearest’插值保留了原始数据的噪声特征，没有进行平滑。
• ‘bilinear’插值提供了轻微的平滑效果，减少了一些噪声。
• ‘bicubic’插值提供了更强的平滑效果，但可能会引入一些伪影。
• ‘gaussian’插值提供了最强的平滑效果，但可能会过度模糊一些细节。

8. 插值与边界效应

在使用插值方法时，我们需要注意边界效应。某些插值方法可能在数据边界处产生不希望的效果。让我们通过一个例子来探讨这个问题：

import numpy as np
import matplotlib.pyplot as plt

# 创建一个有明显边界的数据
data = np.zeros((10, 10))
data[2:8, 2:8] = 1

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

interpolation_methods = ['nearest', 'bilinear', 'bicubic', 'lanczos']

for ax, method in zip(axes.flatten(), interpolation_methods):
    im = ax.imshow(data, interpolation=method, cmap='viridis')
    ax.set_title(f'{method} interpolation - how2matplotlib.com')
    plt.colorbar(im, ax=ax)

plt.tight_layout()
print("不同插值方法在边界处的效果图已生成，请查看图像窗口。")
plt.show()

Output:

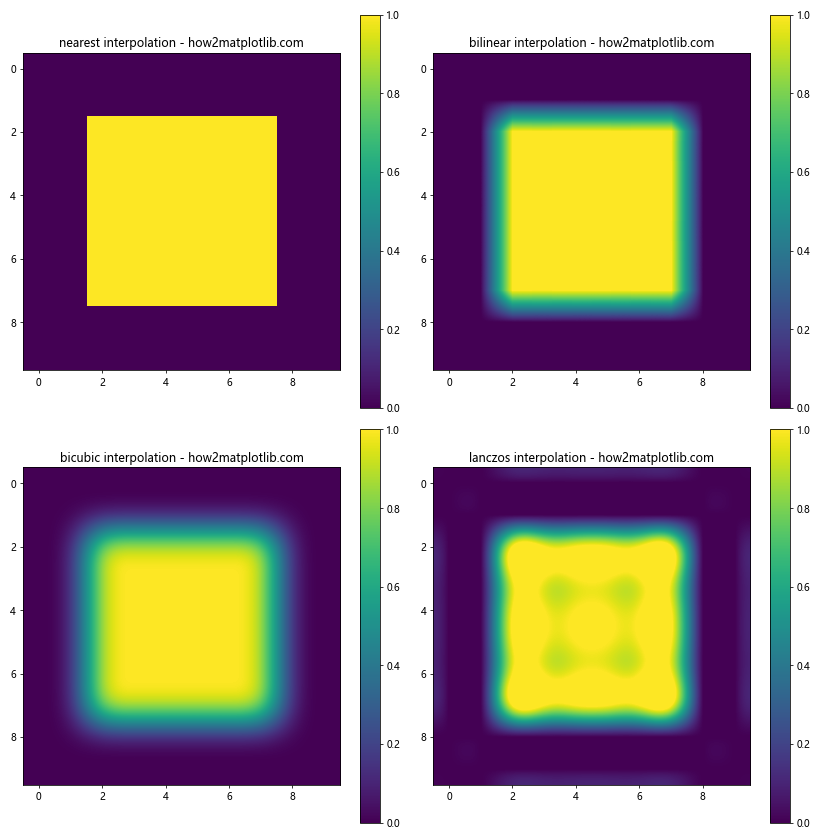
在这个例子中，我们创建了一个10×10的矩阵，其中中心区域为1，周围为0。我们使用四种不同的插值方法来绘制热图，观察它们在边界处的表现：

• ‘nearest’插值在边界处保持锐利的过渡。
• ‘bilinear’插值在边界处产生线性过渡。
• ‘bicubic’和’lanczos’插值在边界处产生更平滑的过渡，但可能会引入一些过冲或振铃效应。

了解这些边界效应对于选择合适的插值方法非常重要，特别是当数据中存在明显的边界或不连续性时。

9. 插值与数据分辨率

数据的分辨率对插值效果有显著影响。对于低分辨率数据，高级插值方法可能会产生更好的视觉效果，而对于高分辨率数据，简单的插值方法可能就足够了。让我们通过一个例子来探讨这个问题：

import numpy as np
import matplotlib.pyplot as plt

# 创建低分辨率和高分辨率数据
low_res_data = np.random.rand(5, 5)
high_res_data = np.random.rand(50, 50)

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

# 低分辨率数据
axes[0, 0].imshow(low_res_data, interpolation='nearest')
axes[0, 0].set_title('Low Res - Nearest - how2matplotlib.com')

axes[0, 1].imshow(low_res_data, interpolation='bicubic')
axes[0, 1].set_title('Low Res - Bicubic - how2matplotlib.com')

# 高分辨率数据
axes[1, 0].imshow(high_res_data, interpolation='nearest')
axes[1, 0].set_title('High Res - Nearest - how2matplotlib.com')

axes[1, 1].imshow(high_res_data, interpolation='bicubic')
axes[1, 1].set_title('High Res - Bicubic - how2matplotlib.com')

for ax in axes.flatten():
    ax.set_xlabel('X-axis')
    ax.set_ylabel('Y-axis')

plt.tight_layout()
print("不同分辨率数据的插值效果对比图已生成，请查看图像窗口。")
plt.show()

Output:

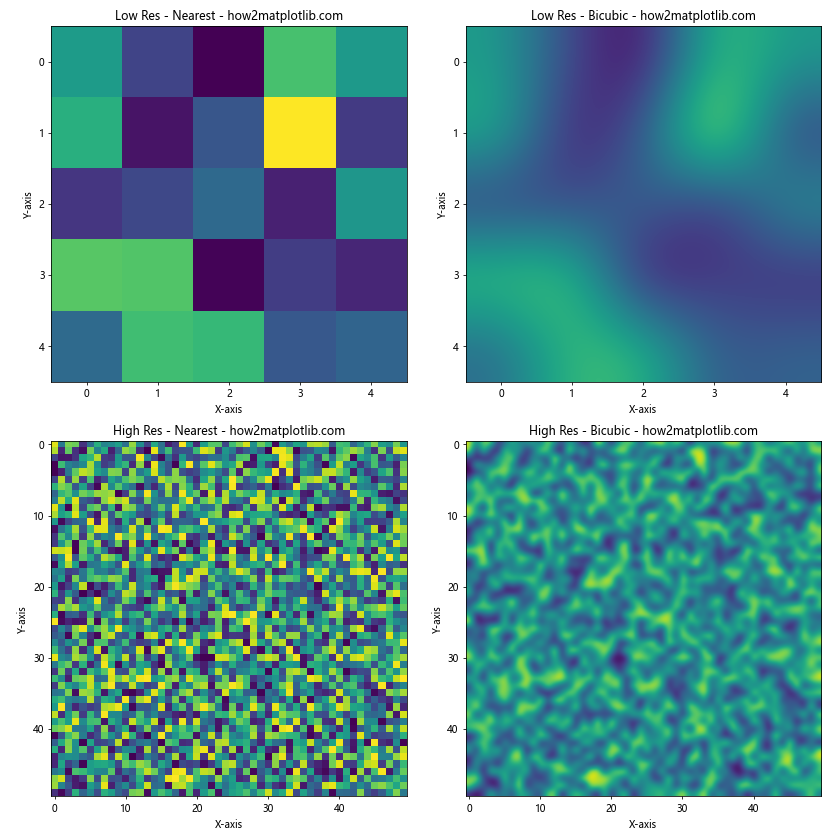
在这个例子中，我们比较了低分辨率（5×5）和高分辨率（50×50）数据在使用’nearest’和’bicubic’插值方法时的效果。可以观察到：

• 对于低分辨率数据，’bicubic’插值提供了明显更平滑的效果。
• 对于高分辨率数据，’nearest’和’bicubic’插值的视觉差异较小。

这说明在处理低分辨率数据时，选择合适的插值方法更为重要，而对于高分辨率数据，简单的插值方法通常就足够了。

10. 插值与性能考虑

在选择插值方法时，我们还需要考虑性能因素。某些高级插值方法可能会显著增加计算时间，特别是对于大型数据集或需要实时渲染的应用。让我们通过一个简单的性能测试来比较不同插值方法的计算时间：

import numpy as np
import matplotlib.pyplot as plt
import time

# 创建一个大型数据集
data = np.random.rand(1000, 1000)

interpolation_methods = ['nearest', 'bilinear', 'bicubic', 'lanczos']

fig, axes = plt.subplots(2, 2, figsize=(12, 12))
axes = axes.flatten()

for ax, method in zip(axes, interpolation_methods):
    start_time = time.time()
    ax.imshow(data, interpolation=method)
    end_time = time.time()

    ax.set_title(f'{method}\nTime: {end_time - start_time:.4f}s - how2matplotlib.com')
    ax.axis('off')

plt.tight_layout()
print("不同插值方法的性能对比图已生成，请查看图像窗口。")
plt.show()

Output:

在这个例子中，我们创建了一个1000×1000的大型随机数据集，并使用四种不同的插值方法来绘制热图。我们记录了每种方法的计算时间，并在图像标题中显示。

通常，我们会观察到以下趋势：
– ‘nearest’插值最快，因为它不需要进行复杂的计算。
– ‘bilinear’插值稍慢，但仍然相对快速。
– ‘bicubic’和’lanczos’插值通常最慢，因为它们涉及更复杂的数学运算。

在实际应用中，需要根据具体需求在图像质量和计算效率之间进行权衡。

11. 自定义插值函数

虽然Matplotlib提供了多种内置的插值方法，但有时我们可能需要自定义插值函数来满足特定需求。虽然Matplotlib不直接支持自定义插值函数，但我们可以通过预处理数据来实现类似的效果。

以下是一个使用自定义插值函数的示例：

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp2d

# 创建原始数据
x = np.linspace(0, 5, 10)
y = np.linspace(0, 5, 10)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)

# 自定义插值函数（这里使用scipy的interp2d作为示例）
f = interp2d(x, y, Z, kind='cubic')

# 创建更高分辨率的网格
x_new = np.linspace(0, 5, 100)
y_new = np.linspace(0, 5, 100)
Z_new = f(x_new, y_new)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

# 原始数据
im1 = ax1.imshow(Z, extent=[0, 5, 0, 5], origin='lower')
ax1.set_title('Original Data - how2matplotlib.com')
plt.colorbar(im1, ax=ax1)

# 插值后的数据
im2 = ax2.imshow(Z_new, extent=[0, 5, 0, 5], origin='lower')
ax2.set_title('Custom Interpolation - how2matplotlib.com')
plt.colorbar(im2, ax=ax2)

plt.tight_layout()
print("自定义插值效果对比图已生成，请查看图像窗口。")
plt.show()

在这个例子中，我们使用了SciPy库的interp2d函数来创建一个自定义的二维插值函数。我们首先创建了一个低分辨率的正弦-余弦波数据，然后使用自定义插值函数将其插值到更高的分辨率。最后，我们比较了原始数据和插值后的数据的可视化效果。

这种方法允许我们使用更复杂的插值算法，或者根据特定需求调整插值过程。

12. 插值与数据类型

不同类型的数据可能需要不同的插值方法。例如，分类数据和连续数据的处理方式应该不同。让我们通过一个例子来说明这一点：

import numpy as np
import matplotlib.pyplot as plt

# 创建分类数据
categorical_data = np.random.randint(0, 5, (10, 10))

# 创建连续数据
continuous_data = np.random.rand(10, 10)

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

# 分类数据 - 不适合插值
axes[0, 0].imshow(categorical_data, interpolation='nearest')
axes[0, 0].set_title('Categorical Data (nearest) - how2matplotlib.com')

axes[0, 1].imshow(categorical_data, interpolation='bilinear')
axes[0, 1].set_title('Categorical Data (bilinear) - how2matplotlib.com')

# 连续数据 - 适合插值
axes[1, 0].imshow(continuous_data, interpolation='nearest')
axes[1, 0].set_title('Continuous Data (nearest) - how2matplotlib.com')

axes[1, 1].imshow(continuous_data, interpolation='bilinear')
axes[1, 1].set_title('Continuous Data (bilinear) - how2matplotlib.com')

for ax in axes.flatten():
    ax.set_xlabel('X-axis')
    ax.set_ylabel('Y-axis')

plt.tight_layout()
print("不同数据类型的插值效果对比图已生成，请查看图像窗口。")
plt.show()

Output:

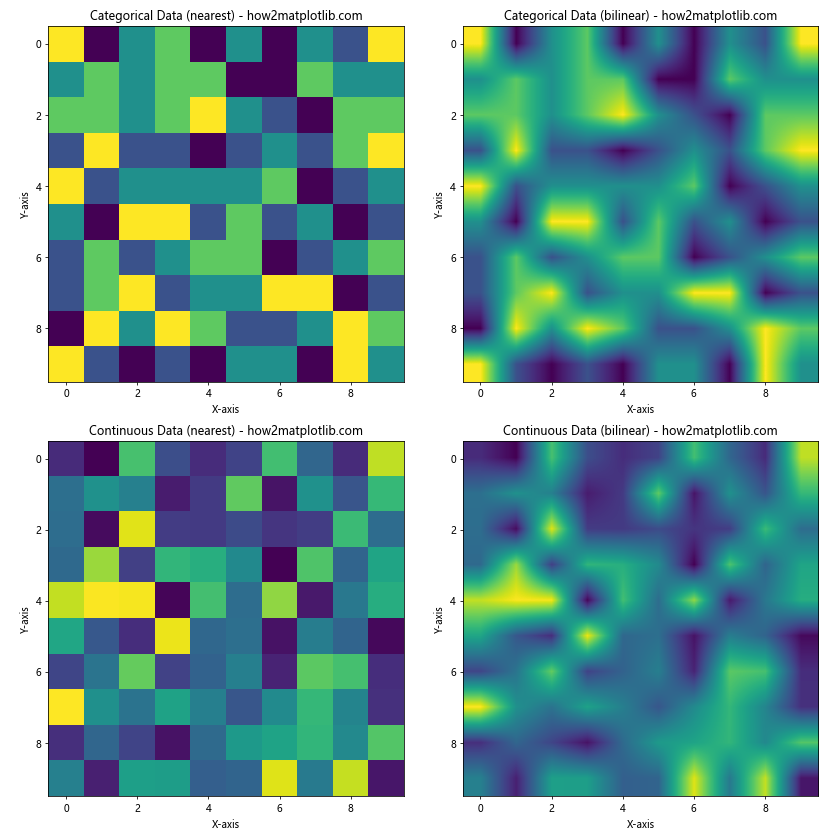
在这个例子中，我们比较了分类数据和连续数据在使用’nearest’和’bilinear’插值方法时的效果。可以观察到：

• 对于分类数据，’nearest’插值是更合适的选择，因为它保持了清晰的边界和离散的类别。
• 对于连续数据，’bilinear’插值提供了更平滑的过渡，更好地表现了数据的连续性。

这个例子强调了根据数据类型选择合适插值方法的重要性。

13. 插值与数据分布

数据的分布特征也会影响插值的效果。例如，均匀分布的数据和具有明显梯度的数据可能需要不同的插值方法。让我们通过一个例子来探讨这个问题：

import numpy as np
import matplotlib.pyplot as plt

# 创建均匀分布的数据
uniform_data = np.random.rand(20, 20)

# 创建具有梯度的数据
x, y = np.meshgrid(np.linspace(0, 1, 20), np.linspace(0, 1, 20))
gradient_data = x * y

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

# 均匀分布数据
axes[0, 0].imshow(uniform_data, interpolation='nearest')
axes[0, 0].set_title('Uniform Data (nearest) - how2matplotlib.com')

axes[0, 1].imshow(uniform_data, interpolation='bicubic')
axes[0, 1].set_title('Uniform Data (bicubic) - how2matplotlib.com')

# 梯度数据
axes[1, 0].imshow(gradient_data, interpolation='nearest')
axes[1, 0].set_title('Gradient Data (nearest) - how2matplotlib.com')

axes[1, 1].imshow(gradient_data, interpolation='bicubic')
axes[1, 1].set_title('Gradient Data (bicubic) - how2matplotlib.com')

for ax in axes.flatten():
    ax.set_xlabel('X-axis')
    ax.set_ylabel('Y-axis')

plt.tight_layout()
print("不同数据分布的插值效果对比图已生成，请查看图像窗口。")
plt.show()

Output:

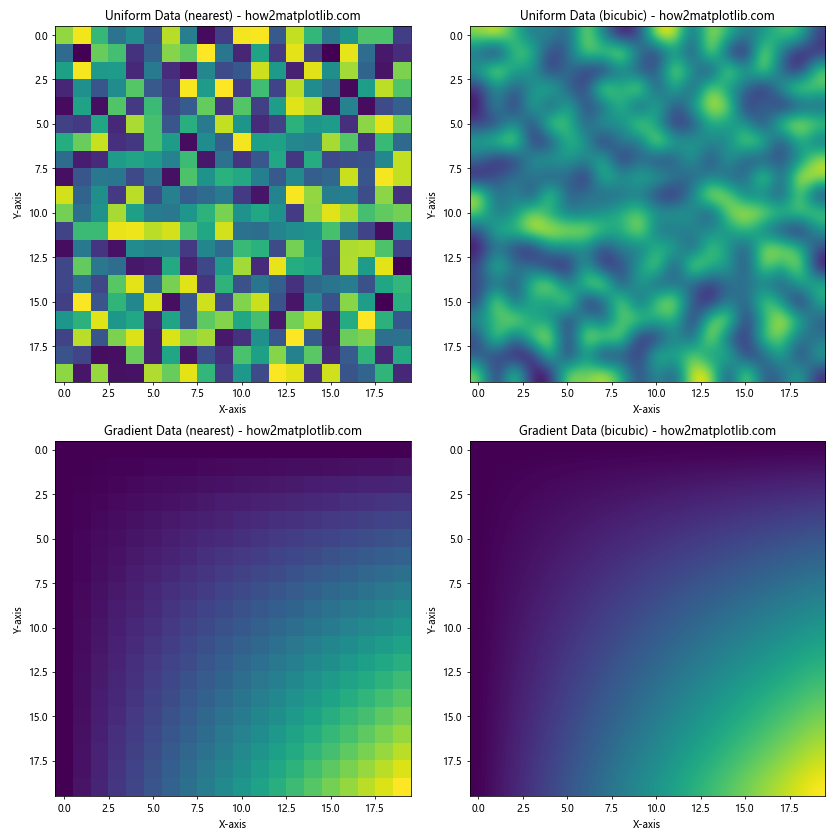
在这个例子中，我们比较了均匀分布的随机数据和具有明显梯度的数据在使用’nearest’和’bicubic’插值方法时的效果。可以观察到：

• 对于均匀分布的数据，’nearest’和’bicubic’插值的差异相对较小。
• 对于具有梯度的数据，’bicubic’插值提供了更平滑的过渡，更好地捕捉了数据的渐变特性。

这个例子说明了数据分布特征对插值效果的影响，强调了在选择插值方法时需要考虑数据的内在结构。## 14. 插值与数据异常值

在实际应用中，数据集可能包含异常值或极端值。这些值可能会对插值结果产生显著影响。让我们通过一个例子来探讨插值方法如何处理异常值：

import numpy as np
import matplotlib.pyplot as plt

# 创建包含异常值的数据
data = np.random.rand(20, 20)
data[5, 5] = 5  # 添加一个异常值

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

interpolation_methods = ['nearest', 'bilinear', 'bicubic', 'gaussian']

for ax, method in zip(axes.flatten(), interpolation_methods):
    im = ax.imshow(data, interpolation=method, cmap='viridis')
    ax.set_title(f'{method} interpolation - how2matplotlib.com')
    plt.colorbar(im, ax=ax)

plt.tight_layout()
print("不同插值方法处理异常值的效果图已生成，请查看图像窗口。")
plt.show()

Output:

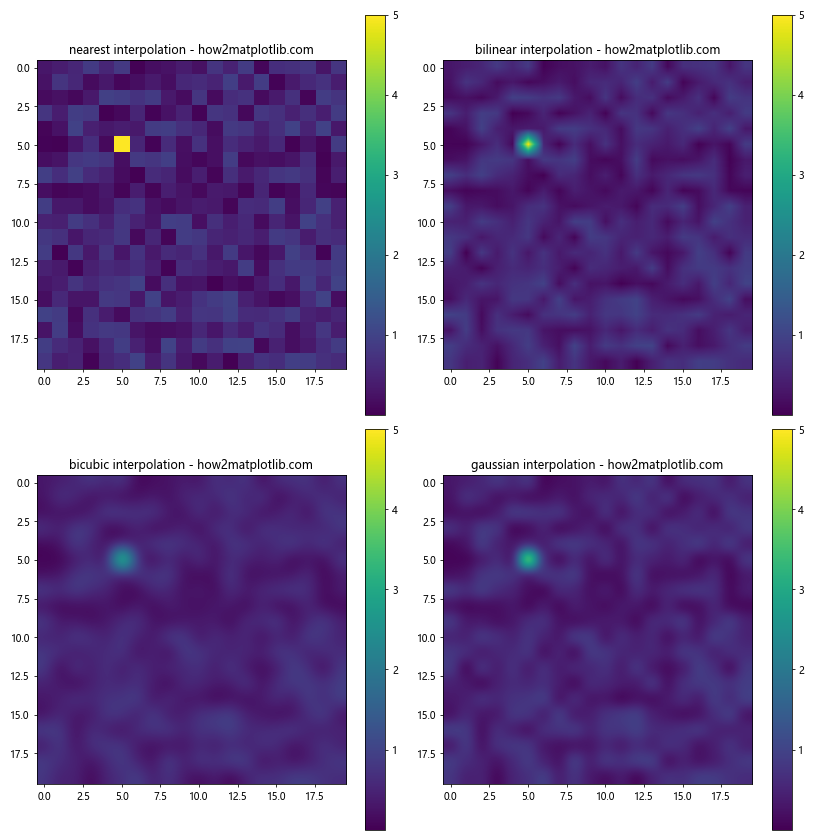
在这个例子中，我们在数据中添加了一个明显的异常值，然后使用不同的插值方法来绘制热图。观察结果，我们可以发现：

• ‘nearest’插值保留了异常值的原始强度，但可能导致周围区域出现突变。
• ‘bilinear’和’bicubic’插值在异常值周围产生了一个过渡区域，但可能会扩大异常值的影响范围。
• ‘gaussian’插值对异常值有一定的平滑效果，但可能会过度模糊周围的数据。

处理包含异常值的数据时，需要谨慎选择插值方法，并考虑是否需要在插值之前对异常值进行预处理。

15. 插值与数据缺失

在实际应用中，我们可能会遇到包含缺失值的数据集。插值可以用来估计这些缺失值，但不同的插值方法可能会产生不同的结果。让我们通过一个例子来探讨这个问题：

import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate

# 创建包含缺失值的数据
x = np.linspace(0, 10, 20)
y = np.linspace(0, 10, 20)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)

# 随机移除一些数据点
mask = np.random.choice([True, False], Z.shape, p=[0.8, 0.2])
Z_missing = np.where(mask, Z, np.nan)

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

# 原始数据
im1 = axes[0, 0].imshow(Z, extent=[0, 10, 0, 10], origin='lower')
axes[0, 0].set_title('Original Data - how2matplotlib.com')
plt.colorbar(im1, ax=axes[0, 0])

# 包含缺失值的数据
im2 = axes[0, 1].imshow(Z_missing, extent=[0, 10, 0, 10], origin='lower')
axes[0, 1].set_title('Data with Missing Values - how2matplotlib.com')
plt.colorbar(im2, ax=axes[0, 1])

# 使用线性插值填充缺失值
x_valid = X[~np.isnan(Z_missing)]
y_valid = Y[~np.isnan(Z_missing)]
z_valid = Z_missing[~np.isnan(Z_missing)]
Z_filled_linear = interpolate.griddata((x_valid, y_valid), z_valid, (X, Y), method='linear')

im3 = axes[1, 0].imshow(Z_filled_linear, extent=[0, 10, 0, 10], origin='lower')
axes[1, 0].set_title('Linear Interpolation - how2matplotlib.com')
plt.colorbar(im3, ax=axes[1, 0])

# 使用最近邻插值填充缺失值
Z_filled_nearest = interpolate.griddata((x_valid, y_valid), z_valid, (X, Y), method='nearest')

im4 = axes[1, 1].imshow(Z_filled_nearest, extent=[0, 10, 0, 10], origin='lower')
axes[1, 1].set_title('Nearest Neighbor Interpolation - how2matplotlib.com')
plt.colorbar(im4, ax=axes[1, 1])

plt.tight_layout()
print("缺失值插值效果对比图已生成，请查看图像窗口。")
plt.show()

Output:

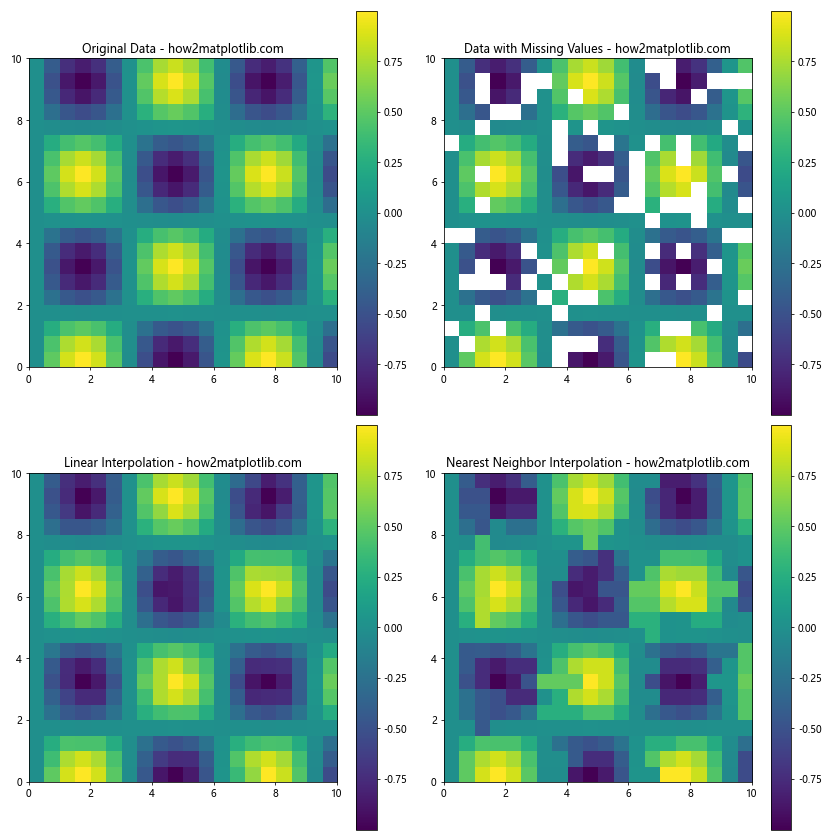
在这个例子中，我们首先创建了一个完整的数据集，然后随机移除了一些数据点来模拟缺失值。我们使用SciPy的griddata函数来执行插值，分别使用线性插值和最近邻插值方法。观察结果，我们可以发现：

• 线性插值在填充缺失值时产生了较为平滑的过渡。
• 最近邻插值保留了更多的原始数据特征，但可能在缺失区域产生不连续的边界。

选择合适的插值方法来处理缺失数据取决于数据的性质和分析的目的。在某些情况下，可能需要结合多种方法或使用更复杂的插值技术。

16. 插值与数据平滑的权衡

插值可以用来平滑数据，但过度平滑可能会导致重要信息的丢失。让我们通过一个例子来探讨插值与数据平滑之间的权衡：

import numpy as np
import matplotlib.pyplot as plt

# 创建带有噪声的数据
x = np.linspace(0, 10, 100)
y = np.sin(x) + np.random.normal(0, 0.1, 100)

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

# 原始数据
axes[0, 0].plot(x, y, 'o-')
axes[0, 0].set_title('Original Data - how2matplotlib.com')

# 使用不同程度的平滑
for i, smooth_factor in enumerate([0.5, 0.1, 0.01]):
    ax = axes[(i+1)//2, (i+1)%2]

    # 使用卷积进行平滑
    window_size = int(len(x) * smooth_factor)
    window = np.ones(window_size) / window_size
    y_smooth = np.convolve(y, window, mode='same')

    ax.plot(x, y, 'o', alpha=0.5, label='Original')
    ax.plot(x, y_smooth, '-', label='Smoothed')
    ax.set_title(f'Smooth Factor: {smooth_factor} - how2matplotlib.com')
    ax.legend()

plt.tight_layout()
print("不同程度平滑效果对比图已生成，请查看图像窗口。")
plt.show()

Output:

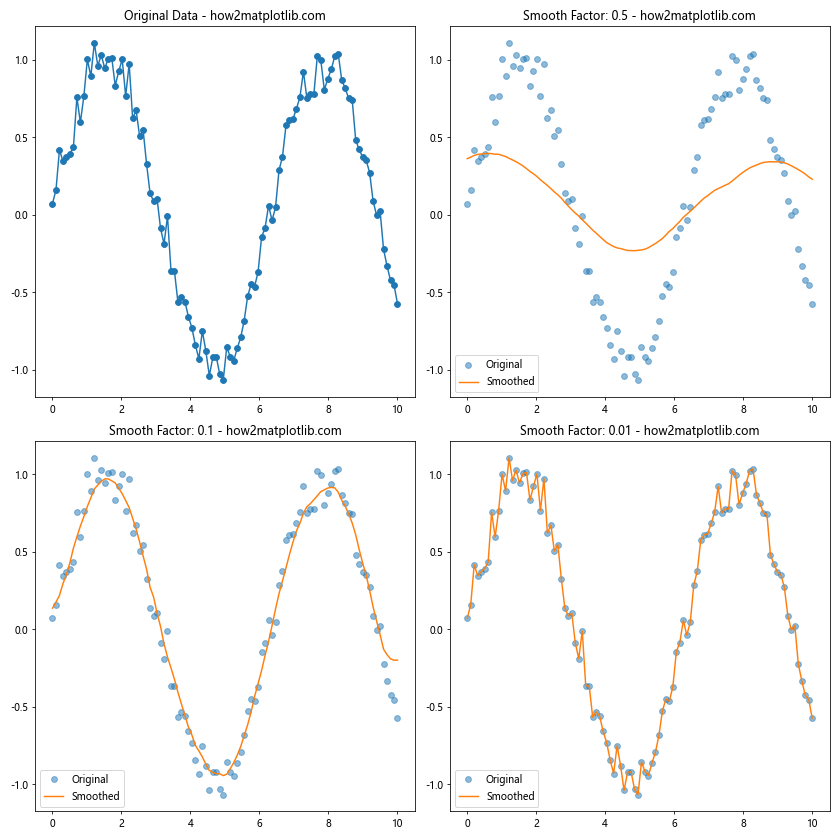
在这个例子中，我们创建了一个带有噪声的正弦波数据，然后使用不同程度的平滑（通过卷积实现）来处理数据。观察结果，我们可以发现：

• 较小的平滑因子（如0.5）保留了更多的原始数据特征，包括噪声。
• 中等的平滑因子（如0.1）在保留主要趋势的同时减少了一些噪声。
• 较大的平滑因子（如0.01）产生了非常平滑的曲线，但可能丢失了一些细节信息。

选择合适的平滑程度需要在保留重要信息和减少噪声之间找到平衡。这个平衡点通常取决于具体的应用场景和数据特征。

17. 插值与图像重采样

插值在图像处理中也扮演着重要角色，特别是在图像重采样（放大或缩小）时。不同的插值方法会产生不同的视觉效果。让我们通过一个例子来探讨这个问题：

import numpy as np
import matplotlib.pyplot as plt

# 创建一个简单的图像
image = np.zeros((10, 10))
image[2:8, 2:8] = 1

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

interpolation_methods = ['nearest', 'bilinear', 'bicubic', 'lanczos']

for ax, method in zip(axes.flatten(), interpolation_methods):
    ax.imshow(image, interpolation=method, cmap='gray')
    ax.set_title(f'{method} interpolation - how2matplotlib.com')
    ax.axis('off')

plt.tight_layout()
print("不同插值方法的图像重采样效果图已生成，请查看图像窗口。")
plt.show()

Output:

在这个例子中，我们创建了一个简单的10×10的二值图像，然后使用不同的插值方法将其放大显示。观察结果，我们可以发现：

• ‘nearest’插值保持了锐利的边缘，但可能产生块状效果。
• ‘bilinear’插值产生了较为平滑的过渡，但可能使边缘变得模糊。
• ‘bicubic’和’lanczos’插值提供了更平滑的过渡，同时尝试保持一些边缘锐利度。

在实际应用中，选择合适的插值方法取决于具体需求。例如，对于需要保持锐利边缘的图像（如文本或图标），’nearest’插值可能更合适；而对于需要平滑过渡的照片类图像，’bicubic’或’lanczos’插值可能会产生更好的效果。

18. 插值与数据趋势分析

插值不仅可以用于可视化，还可以帮助我们分析数据趋势。不同的插值方法可能会影响我们对数据趋势的理解。让我们通过一个例子来探讨这个问题：

import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate

# 创建一些散点数据
np.random.seed(0)
x = np.linspace(0, 10, 20)
y = np.sin(x) + np.random.normal(0, 0.1, 20)

# 创建更密集的x值用于插值
x_dense = np.linspace(0, 10, 200)

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

interpolation_methods = ['linear', 'nearest', 'cubic', 'quadratic']

for ax, method in zip(axes.flatten(), interpolation_methods):
    f = interpolate.interp1d(x, y, kind=method)
    y_interp = f(x_dense)

    ax.plot(x, y, 'o', label='Data')
    ax.plot(x_dense, y_interp, '-', label='Interpolation')
    ax.set_title(f'{method.capitalize()} Interpolation - how2matplotlib.com')
    ax.legend()
    ax.set_xlabel('X-axis')
    ax.set_ylabel('Y-axis')

plt.tight_layout()
print("不同插值方法的数据趋势分析效果图已生成，请查看图像窗口。")
plt.show()

Output:

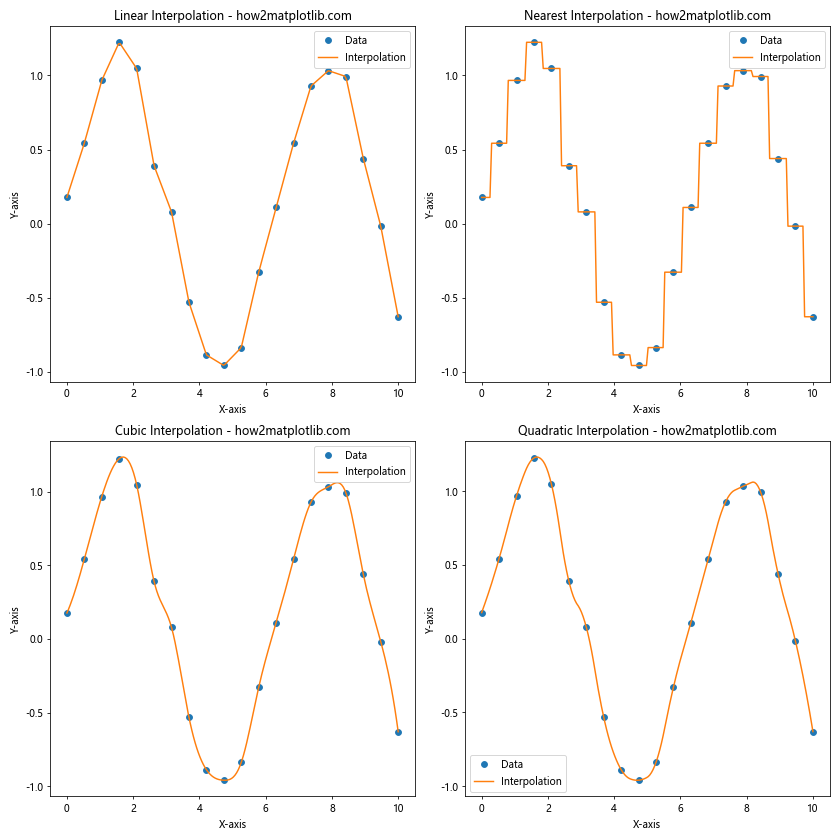
在这个例子中，我们创建了一些带有噪声的正弦波数据点，然后使用不同的插值方法来分析数据趋势。观察结果，我们可以发现：

• 线性插值提供了一个简单的趋势估计，但可能错过一些曲线特征。
• 最近邻插值保留了原始数据点的值，但产生了阶梯状的趋势线。
• 三次插值（cubic）产生了平滑的曲线，可能更好地捕捉了数据的整体趋势。
• 二次插值（quadratic）在平滑度和灵活性之间提供了一个折中方案。

选择合适的插值方法进行趋势分析时，需要考虑数据的性质、噪声水平以及我们对趋势的预期。有时，可能需要尝试多种方法并结合领域知识来得出最合理的结论。

19. 插值与数据预测

插值还可以用于简单的数据预测任务。虽然不如专门的预测模型复杂，但在某些情况下，插值可以提供快速的预测估计。让我们通过一个例子来探讨如何使用插值进行简单的数据预测：

import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate

# 创建一些时间序列数据
np.random.seed(0)
x = np.arange(0, 10, 0.5)
y = np.sin(x) + np.random.normal(0, 0.1, len(x))

# 用于预测的新x值
x_pred = np.arange(10, 15, 0.5)

fig, axes = plt.subplots(2, 2, figsize=(12, 12))

interpolation_methods = ['linear', 'nearest', 'cubic', 'quadratic']

for ax, method in zip(axes.flatten(), interpolation_methods):
    f = interpolate.interp1d(x, y, kind=method, fill_value='extrapolate')
    y_pred = f(x_pred)

    ax.plot(x, y, 'o', label='Data')
    ax.plot(x_pred, y_pred, 's-', label='Prediction')
    ax.axvline(x=10, color='r', linestyle='--', label='Prediction Start')
    ax.set_title(f'{method.capitalize()} Interpolation - how2matplotlib.com')
    ax.legend()
    ax.set_xlabel('X-axis')
    ax.set_ylabel('Y-axis')

plt.tight_layout()
print("不同插值方法的数据预测效果图已生成，请查看图像窗口。")
plt.show()

Output:

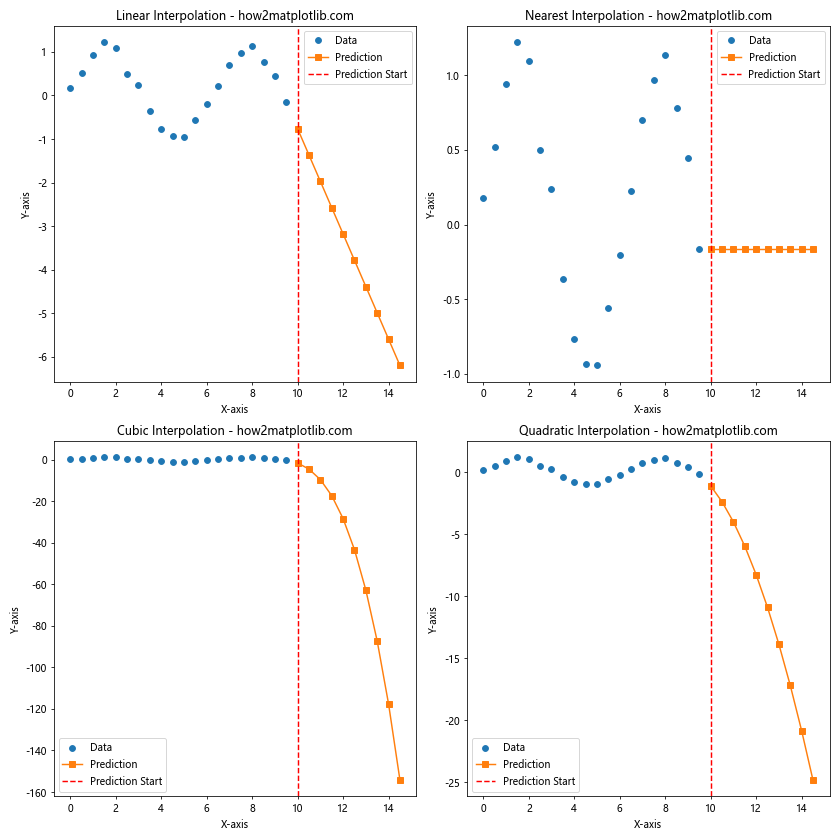
在这个例子中，我们创建了一个简单的时间序列数据，然后使用不同的插值方法来预测未来的值。观察结果，我们可以发现：

• 线性插值提供了一个简单的线性外推预测。
• 最近邻插值将最后一个已知值延伸到未来，这可能不太合理。
• 三次插值（cubic）和二次插值（quadratic）提供了更复杂的非线性预测，但可能在远离已知数据的地方产生不合理的波动。

需要注意的是，这种基于插值的简单预测方法在实际应用中可能不够可靠，特别是对于复杂的时间序列数据。在进行真正的预测任务时，通常需要使用更复杂的时间序列分析方法或机器学习模型。

20. 插值与数据可视化的艺术性

插值不仅是一种技术手段，还可以成为创造艺术效果的工具。通过巧妙地选择和组合不同的插值方法，我们可以创造出独特的视觉效果。让我们通过一个例子来探索插值的艺术潜力：

import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate

# 创建一些随机数据点
np.random.seed(42)
x = np.random.rand(20)
y = np.random.rand(20)
z = np.random.rand(20)

# 创建网格
xi = yi = np.linspace(0, 1, 100)
XI, YI = np.meshgrid(xi, yi)

# 使用不同的插值方法
methods = ['nearest', 'linear', 'cubic']
fig, axes = plt.subplots(1, 3, figsize=(18, 6))

for ax, method in zip(axes, methods):
    # 插值
    ZI = interpolate.griddata((x, y), z, (XI, YI), method=method)

    # 绘制热图
    im = ax.imshow(ZI, extent=[0, 1, 0, 1], origin='lower', cmap='viridis')
    ax.plot(x, y, 'ko', ms=3)  # 原始数据点
    ax.set_title(f'{method.capitalize()} Interpolation - how2matplotlib.com')
    ax.set_xlabel('X-axis')
    ax.set_ylabel('Y-axis')
    plt.colorbar(im, ax=ax)

plt.tight_layout()
print("艺术化插值效果图已生成，请查看图像窗口。")
plt.show()

Output:

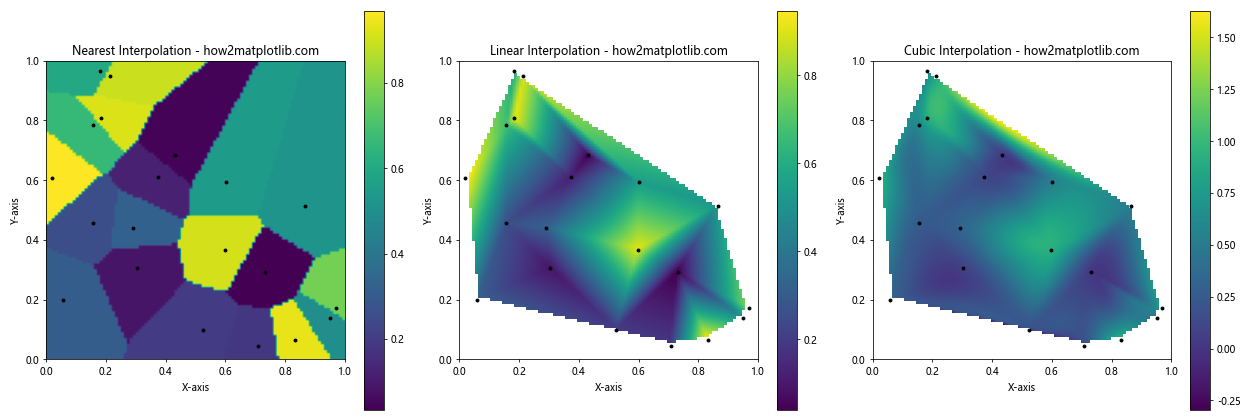
在这个例子中，我们创建了一些随机的数据点，然后使用不同的插值方法来创建连续的色彩场。观察结果，我们可以发现：

• 最近邻插值创造了一种块状、马赛克般的效果。
• 线性插值产生了更加平滑的过渡，但仍保留了一些几何特征。
• 三次插值创造了最为平滑和流畅的效果，呈现出一种有机的感觉。

这种艺术化的数据可视化可以用于创造独特的背景、纹理或抽象艺术作品。通过调整颜色映射、数据点的分布和插值方法，可以创造出各种有趣的视觉效果。

总结

通过本文的详细探讨，我们深入了解了Matplotlib中热图插值技术的方方面面。从基本概念到高级应用，我们涵盖了以下关键点：

1. 热图的基本原理和创建方法
2. 插值的概念及其在热图中的重要性
3. Matplotlib提供的各种插值方法及其特点
4. 如何选择合适的插值方法
5. 插值与图像缩放的关系
6. 插值与颜色映射的相互作用
7. 插值在数据平滑中的应用
8. 插值对边界效应的影响
9. 插值与数据分辨率的关系
10. 插值方法的性能考虑
11. 自定义插值函数的实现
12. 插值在不同数据类型中的应用
13. 插值对数据分布的影响
14. 插值在处理异常值和缺失数据中的作用
15. 插值与数据平滑之间的权衡
16. 插值在图像重采样中的应用
17. 插值在数据趋势分析中的作用
18. 使用插值进行简单的数据预测
19. 插值在创造艺术效果中的潜力

通过这些探讨，我们不仅掌握了如何技术性地使用Matplotlib的热图插值功能，还了解了如何根据具体需求选择和调整插值方法。插值技术不仅是数据可视化的重要工具，还可以成为数据分析、预测和艺术创作的有力辅助。

在实际应用中，选择合适的插值方法需要考虑多个因素，包括数据的性质、分析的目的、视觉效果的需求以及计算效率等。通过不断实践和探索，我们可以更好地利用插值技术来增强我们的数据可视化和分析能力。

最后，值得注意的是，虽然插值可以帮助我们更好地理解和展示数据，但它也可能引入偏差或误导性的信息。因此，在使用插值技术时，我们需要保持批判性思维，并始终将插值结果与原始数据进行对比和验证。