如何使用Matplotlib在Python中绘制复数

如何使用Matplotlib在Python中绘制复数

参考：How to plot a complex number in Python using Matplotlib

复数是数学和科学中的重要概念，它们在许多领域都有广泛的应用，如信号处理、电气工程和量子力学等。在Python中，我们可以使用Matplotlib库来可视化复数，这不仅能帮助我们更好地理解复数的性质，还能直观地展示复数在各种应用中的行为。本文将详细介绍如何使用Matplotlib在Python中绘制复数，包括复平面上的点、向量表示、复数函数的图像等多个方面。

1. 复数的基本概念

在开始绘制复数之前，我们先简要回顾一下复数的基本概念。复数由实部和虚部组成，通常表示为 a + bi 的形式，其中 a 是实部，b 是虚部，i 是虚数单位（i² = -1）。在复平面上，实部对应 x 轴，虚部对应 y 轴。

在Python中，我们可以使用内置的 complex 类型来表示复数。下面是一个简单的例子：

import matplotlib.pyplot as plt

# 创建一个复数
z = 3 + 4j

# 打印复数的实部和虚部
print(f"Real part: {z.real}")
print(f"Imaginary part: {z.imag}")

# 绘制复数点
plt.figure(figsize=(8, 6))
plt.scatter(z.real, z.imag, color='red', s=100)
plt.axhline(y=0, color='k', linestyle='--')
plt.axvline(x=0, color='k', linestyle='--')
plt.xlabel('Real')
plt.ylabel('Imaginary')
plt.title('Complex Number Representation - how2matplotlib.com')
plt.grid(True)
plt.show()

Output:

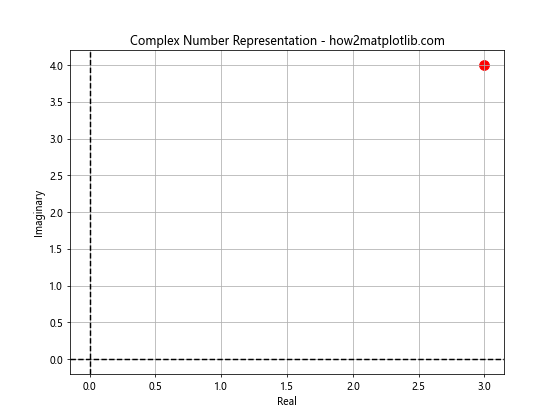
在这个例子中，我们创建了一个复数 3+4i，并打印了它的实部和虚部。然后，我们使用 Matplotlib 的 scatter 函数在复平面上绘制了这个点。axhline 和 axvline 函数用于绘制坐标轴。

2. 在复平面上绘制多个复数

当我们需要比较或分析多个复数时，在同一个复平面上绘制它们会很有帮助。以下是一个绘制多个复数的例子：

import matplotlib.pyplot as plt
import numpy as np

# 创建多个复数
z1 = 2 + 3j
z2 = -1 + 2j
z3 = 3 - 1j

# 将复数放入列表中
complex_numbers = [z1, z2, z3]

# 提取实部和虚部
real_parts = [z.real for z in complex_numbers]
imag_parts = [z.imag for z in complex_numbers]

# 绘制复数点
plt.figure(figsize=(10, 8))
plt.scatter(real_parts, imag_parts, color=['red', 'blue', 'green'], s=100)

# 添加标签
for i, z in enumerate(complex_numbers):
    plt.annotate(f'z{i+1}', (z.real, z.imag), xytext=(5, 5), textcoords='offset points')

plt.axhline(y=0, color='k', linestyle='--')
plt.axvline(x=0, color='k', linestyle='--')
plt.xlabel('Real')
plt.ylabel('Imaginary')
plt.title('Multiple Complex Numbers - how2matplotlib.com')
plt.grid(True)
plt.show()

Output:

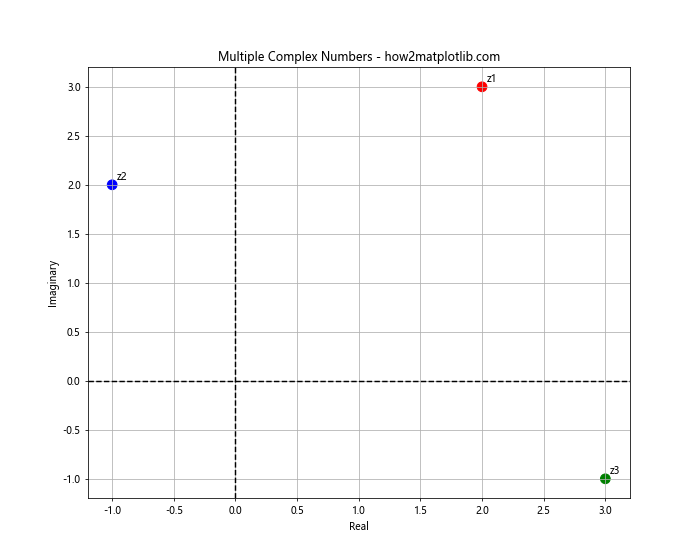
在这个例子中，我们创建了三个复数，并将它们放入一个列表中。然后，我们提取了每个复数的实部和虚部，用不同的颜色在复平面上绘制了这些点。我们还使用 annotate 函数为每个点添加了标签。

3. 复数的向量表示

复数也可以用向量来表示，这种表示方法在某些应用中特别有用，比如在描述旋转或相位时。以下是一个使用向量表示复数的例子：

import matplotlib.pyplot as plt
import numpy as np

# 创建一个复数
z = 4 + 3j

# 计算复数的模和辐角
magnitude = np.abs(z)
angle = np.angle(z)

# 绘制复数向量
plt.figure(figsize=(10, 8))
plt.quiver(0, 0, z.real, z.imag, angles='xy', scale_units='xy', scale=1, color='red')

# 绘制虚线表示投影
plt.plot([0, z.real], [0, 0], 'k--')
plt.plot([z.real, z.real], [0, z.imag], 'k--')

# 添加标签
plt.text(z.real/2, -0.5, f'Real: {z.real}', ha='center')
plt.text(z.real+0.5, z.imag/2, f'Imag: {z.imag}', va='center')
plt.text(z.real/2, z.imag/2, f'|z| = {magnitude:.2f}\nθ = {np.degrees(angle):.2f}°', ha='center', va='center')

plt.axhline(y=0, color='k', linestyle='--')
plt.axvline(x=0, color='k', linestyle='--')
plt.xlabel('Real')
plt.ylabel('Imaginary')
plt.title('Complex Number as a Vector - how2matplotlib.com')
plt.grid(True)
plt.axis('equal')
plt.show()

Output:

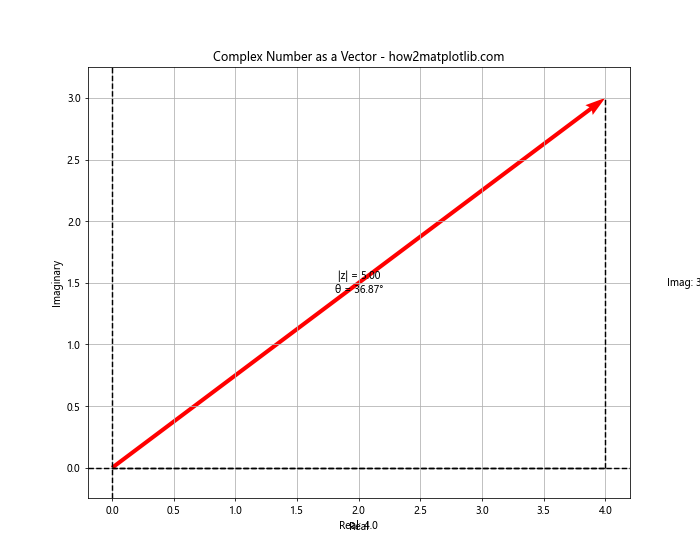
在这个例子中，我们使用 quiver 函数绘制了表示复数的向量。我们还计算了复数的模（magnitude）和辐角（angle），并在图上显示了这些信息。虚线表示向量在实轴和虚轴上的投影。

4. 绘制复数函数

复数函数是输入和输出都是复数的函数。绘制复数函数可以帮助我们理解函数的行为。以下是一个绘制复数函数的例子：

import matplotlib.pyplot as plt
import numpy as np

def complex_function(z):
    return z**2 + 1

# 创建复平面上的点
x = np.linspace(-2, 2, 20)
y = np.linspace(-2, 2, 20)
X, Y = np.meshgrid(x, y)
Z = X + Y*1j

# 计算函数值
W = complex_function(Z)

# 绘制函数的实部和虚部
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

# 绘制实部
c1 = ax1.contourf(X, Y, W.real, cmap='viridis')
ax1.set_title('Real Part of f(z) = z² + 1 - how2matplotlib.com')
ax1.set_xlabel('Real')
ax1.set_ylabel('Imaginary')
fig.colorbar(c1, ax=ax1)

# 绘制虚部
c2 = ax2.contourf(X, Y, W.imag, cmap='plasma')
ax2.set_title('Imaginary Part of f(z) = z² + 1 - how2matplotlib.com')
ax2.set_xlabel('Real')
ax2.set_ylabel('Imaginary')
fig.colorbar(c2, ax=ax2)

plt.tight_layout()
plt.show()

Output:

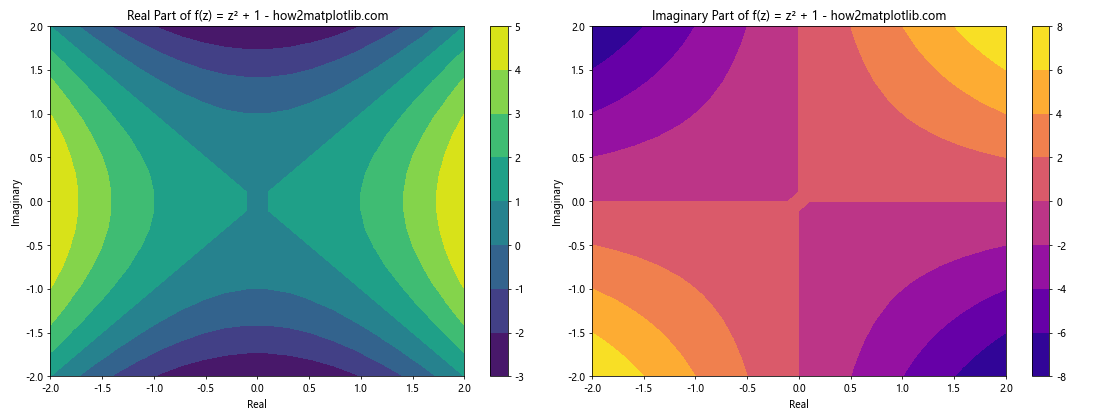
在这个例子中，我们定义了一个复数函数 f(z) = z² + 1，然后在复平面上的一个网格上计算了这个函数的值。我们使用 contourf 函数分别绘制了函数的实部和虚部，使用不同的颜色图来区分。

5. 复数的极坐标表示

复数也可以用极坐标形式表示，这在某些应用中很有用，比如在处理周期性函数时。以下是一个使用极坐标表示复数的例子：

import matplotlib.pyplot as plt
import numpy as np

# 创建一个复数
z = 3 + 4j

# 计算极坐标
r = np.abs(z)
theta = np.angle(z)

# 创建极坐标图
fig, ax = plt.subplots(subplot_kw=dict(projection='polar'), figsize=(8, 8))

# 绘制复数点
ax.plot(theta, r, 'ro')

# 绘制从原点到复数点的线
ax.plot([0, theta], [0, r], 'r-')

# 添加标签
ax.text(theta, r, f'z = {z}', ha='right', va='bottom')
ax.text(theta/2, r/2, f'r = {r:.2f}\nθ = {np.degrees(theta):.2f}°', ha='left', va='top')

ax.set_title('Complex Number in Polar Coordinates - how2matplotlib.com')
plt.show()

Output:

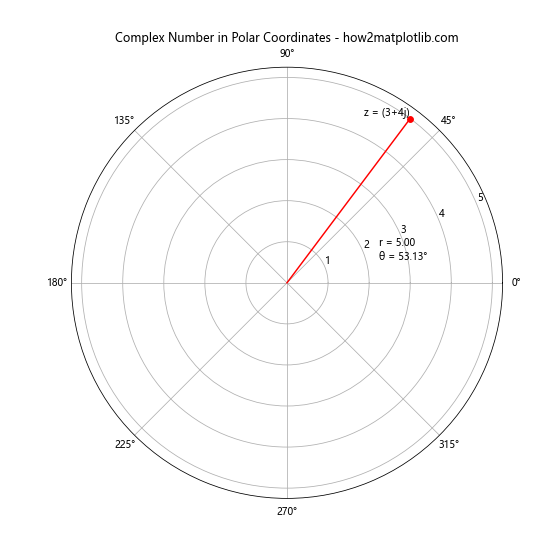
在这个例子中，我们使用 abs 和 angle 函数计算了复数的模和辐角，然后使用极坐标系统绘制了复数点。我们还添加了一条从原点到复数点的线，以及相关的标签信息。

6. 复数的指数形式

复数的指数形式（也称为欧拉形式）是 z = r * e^(iθ)，其中 r 是复数的模，θ 是辐角。这种形式在某些数学和物理应用中特别有用。以下是一个展示复数指数形式的例子：

import matplotlib.pyplot as plt
import numpy as np

# 创建一个复数
z = 2 * np.exp(1j * np.pi/4)

# 计算模和辐角
r = np.abs(z)
theta = np.angle(z)

# 创建图形
fig, ax = plt.subplots(figsize=(10, 8))

# 绘制单位圆
circle = plt.Circle((0, 0), 1, fill=False)
ax.add_artist(circle)

# 绘制复数向量
ax.quiver(0, 0, z.real, z.imag, angles='xy', scale_units='xy', scale=1, color='red')

# 绘制辐角弧
arc = np.linspace(0, theta, 100)
ax.plot(np.cos(arc), np.sin(arc), 'b--')

# 添加标签
ax.text(z.real, z.imag, f'z = {r:.2f}e^({theta:.2f}i)', ha='right', va='bottom')
ax.text(0.5*np.cos(theta/2), 0.5*np.sin(theta/2), f'θ = {np.degrees(theta):.2f}°', ha='center', va='center')

ax.set_xlim(-2.5, 2.5)
ax.set_ylim(-2.5, 2.5)
ax.set_aspect('equal')
ax.grid(True)
ax.set_title('Complex Number in Exponential Form - how2matplotlib.com')
ax.set_xlabel('Real')
ax.set_ylabel('Imaginary')

plt.show()

Output:

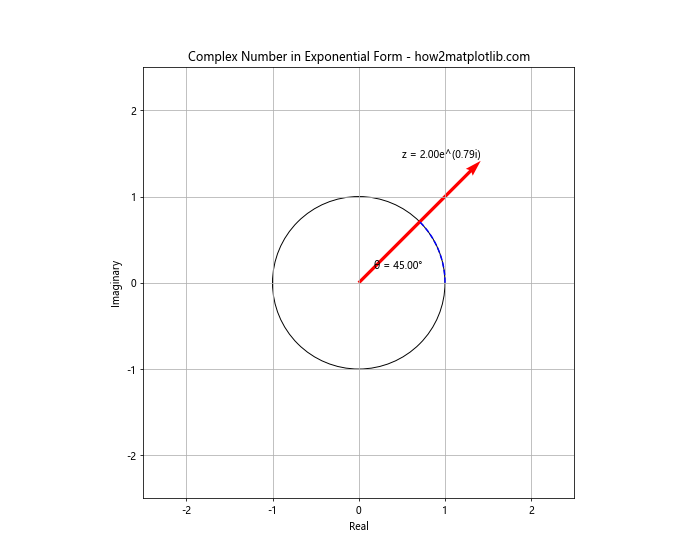
在这个例子中，我们创建了一个复数 z = 2 * e^(iπ/4)，然后在复平面上绘制了它。我们还绘制了单位圆和表示辐角的弧，以更好地展示复数的指数形式。

7. 复数的旋转

复数乘法可以用来表示旋转。当我们将一个复数乘以 e^(iθ) 时，它会围绕原点旋转 θ 弧度。以下是一个展示复数旋转的例子：

import matplotlib.pyplot as plt
import numpy as np

# 初始复数
z = 2 + 1j

# 旋转角度（弧度）
angles = np.linspace(0, 2*np.pi, 8, endpoint=False)

# 创建图形
fig, ax = plt.subplots(figsize=(10, 10))

# 绘制原始复数
ax.quiver(0, 0, z.real, z.imag, angles='xy', scale_units='xy', scale=1, color='red', label='Original')

# 绘制旋转后的复数
for i, angle in enumerate(angles):
    rotated_z = z * np.exp(1j * angle)
    ax.quiver(0, 0, rotated_z.real, rotated_z.imag, angles='xy', scale_units='xy', scale=1, 
              color=plt.cm.viridis(i/len(angles)), label=f'Rotated {np.degrees(angle):.0f}°')

ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)
ax.set_aspect('equal')
ax.grid(True)
ax.set_title('Complex Number Rotation - how2matplotlib.com')
ax.set_xlabel('Real')
ax.set_ylabel('Imaginary')
ax.legend(loc='upper left', bbox_to_anchor=(1, 1))

plt.tight_layout()
plt.show()

Output:

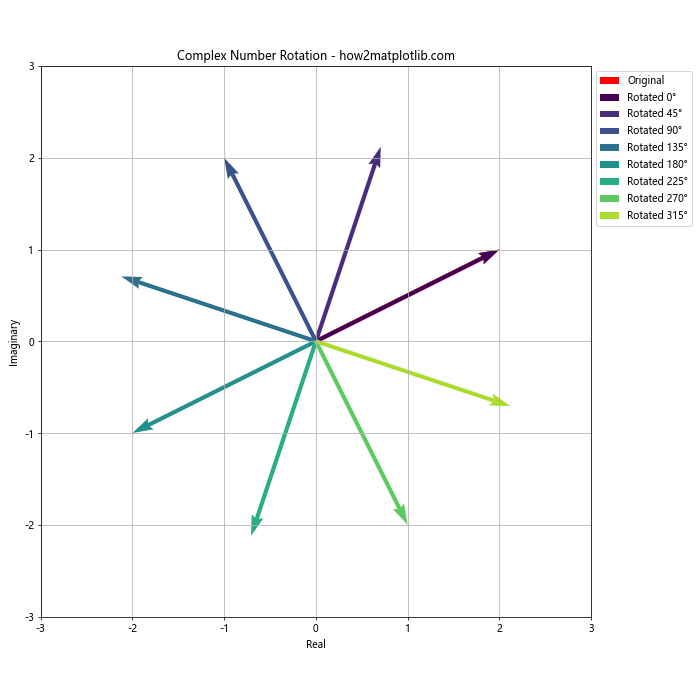
在这个例子中，我们从一个初始复数开始，然后将其旋转不同的角度。我们使用 quiver 函数绘制了原始复数和旋转后的复数，使用不同的颜色来区分不同的旋转角度。

8. 复数的幂函数

复数的幂函数可以产生有趣的图案。以下是一个绘制复数幂函数的例子：

import matplotlib.pyplot as plt
import numpy as np

def complex_power(z, n):
    return z**n

# 创建复平面上的点
x = np.linspace(-2, 2, 400)
y = np.linspace(-2, 2, 400)
X, Y = np.meshgrid(x, y)
Z = X + Y*1j

# 计算幂函数
n = 3  # 幂
W = complex_power(Z, n)

# 绘制幂函数
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

# 绘制实部
c1 = ax1.imshow(np.real(W), extent=[-2, 2, -2, 2], cmap='viridis', origin='lower')
ax1.set_title(f'Real Part of z^{n} - how2matplotlib.com')
ax1.set_xlabel('Real')
ax1.set_ylabel('Imaginary')
fig.colorbar(c1, ax=ax1)

# 绘制虚部
c2 = ax2.imshow(np.imag(W), extent=[-2, 2, -2, 2], cmap='plasma', origin='lower')
ax2.set_title(f'Imaginary Part of z^{n} - how2matplotlib.com')
ax2.set_xlabel('Real')
ax2.set_ylabel('Imaginary')
fig.colorbar(c2, ax=ax2)

plt.tight_layout()
plt.show()

在这个例子中，我们定义了一个复数幂函数 z^n，然后在复平面上的一个网格上计算了这个函数的值。我们使用 imshow 函数分别绘制了函数的实部和虚部，使用不同的颜色图来区分。这种可视化方法可以帮助我们理解复数幂函数的行为和特性。

9. 复数的根

复数的根是另一个有趣的主题。对于一个复数 z 和一个正整数 n，z 的 n 次根是满足 w^n = z 的所有复数 w。以下是一个绘制复数根的例子：

import matplotlib.pyplot as plt
import numpy as np

def complex_roots(z, n):
    r = np.abs(z)**(1/n)
    theta = np.angle(z)
    roots = [r * np.exp(1j * (theta + 2*k*np.pi) / n) for k in range(n)]
    return roots

# 创建一个复数
z = 1 + 1j

# 计算根
n = 5  # 5次根
roots = complex_roots(z, n)

# 绘制复数根
plt.figure(figsize=(10, 10))
plt.scatter(z.real, z.imag, color='red', s=100, label='Original')
for i, root in enumerate(roots):
    plt.scatter(root.real, root.imag, color='blue', s=100, label=f'Root {i+1}')
    plt.plot([0, root.real], [0, root.imag], 'b--')

plt.axhline(y=0, color='k', linestyle='--')
plt.axvline(x=0, color='k', linestyle='--')
plt.xlabel('Real')
plt.ylabel('Imaginary')
plt.title(f'{n}th Roots of Complex Number - how2matplotlib.com')
plt.legend()
plt.grid(True)
plt.axis('equal')
plt.show()

在这个例子中，我们定义了一个函数来计算复数的 n 次根。然后，我们绘制了原始复数和它的所有 n 次根。虚线表示从原点到每个根的向量。这种可视化可以帮助我们理解复数根的几何意义。

10. 复数的对数

复数的对数是另一个重要的概念。对于一个非零复数 z，它的主对数定义为 log(z) = ln|z| + i*arg(z)，其中 arg(z) 是 z 的主辐角（-π < arg(z) ≤ π）。以下是一个绘制复数对数的例子：

import matplotlib.pyplot as plt
import numpy as np

def complex_log(z):
    return np.log(np.abs(z)) + 1j * np.angle(z)

# 创建复平面上的点
x = np.linspace(-3, 3, 300)
y = np.linspace(-3, 3, 300)
X, Y = np.meshgrid(x, y)
Z = X + Y*1j

# 计算对数
W = complex_log(Z)

# 绘制对数函数
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

# 绘制实部
c1 = ax1.imshow(np.real(W), extent=[-3, 3, -3, 3], cmap='viridis', origin='lower')
ax1.set_title('Real Part of log(z) - how2matplotlib.com')
ax1.set_xlabel('Real')
ax1.set_ylabel('Imaginary')
fig.colorbar(c1, ax=ax1)

# 绘制虚部
c2 = ax2.imshow(np.imag(W), extent=[-3, 3, -3, 3], cmap='plasma', origin='lower')
ax2.set_title('Imaginary Part of log(z) - how2matplotlib.com')
ax2.set_xlabel('Real')
ax2.set_ylabel('Imaginary')
fig.colorbar(c2, ax=ax2)

plt.tight_layout()
plt.show()

在这个例子中，我们定义了一个复数对数函数，然后在复平面上的一个网格上计算了这个函数的值。我们使用 imshow 函数分别绘制了函数的实部和虚部。这种可视化可以帮助我们理解复数对数函数的行为，包括它的分支切割。

11. 复数的三角函数

复数也可以应用于三角函数。复数的正弦、余弦等函数有着有趣的性质。以下是一个绘制复数正弦函数的例子：

import matplotlib.pyplot as plt
import numpy as np

# 创建复平面上的点
x = np.linspace(-2*np.pi, 2*np.pi, 300)
y = np.linspace(-2, 2, 300)
X, Y = np.meshgrid(x, y)
Z = X + Y*1j

# 计算复数正弦
W = np.sin(Z)

# 绘制复数正弦函数
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

# 绘制实部
c1 = ax1.imshow(np.real(W), extent=[-2*np.pi, 2*np.pi, -2, 2], cmap='viridis', origin='lower', aspect='auto')
ax1.set_title('Real Part of sin(z) - how2matplotlib.com')
ax1.set_xlabel('Real')
ax1.set_ylabel('Imaginary')
fig.colorbar(c1, ax=ax1)

# 绘制虚部
c2 = ax2.imshow(np.imag(W), extent=[-2*np.pi, 2*np.pi, -2, 2], cmap='plasma', origin='lower', aspect='auto')
ax2.set_title('Imaginary Part of sin(z) - how2matplotlib.com')
ax2.set_xlabel('Real')
ax2.set_ylabel('Imaginary')
fig.colorbar(c2, ax=ax2)

plt.tight_layout()
plt.show()

在这个例子中，我们在复平面上计算了正弦函数的值，并分别绘制了它的实部和虚部。这种可视化可以帮助我们理解复数正弦函数的周期性和其他性质。

12. 复数的指数函数

复数的指数函数 e^z 是另一个重要的函数，它与三角函数有着密切的关系。以下是一个绘制复数指数函数的例子：

import matplotlib.pyplot as plt
import numpy as np

# 创建复平面上的点
x = np.linspace(-2, 2, 300)
y = np.linspace(-2, 2, 300)
X, Y = np.meshgrid(x, y)
Z = X + Y*1j

# 计算复数指数
W = np.exp(Z)

# 绘制复数指数函数
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

# 绘制实部
c1 = ax1.imshow(np.real(W), extent=[-2, 2, -2, 2], cmap='viridis', origin='lower')
ax1.set_title('Real Part of exp(z) - how2matplotlib.com')
ax1.set_xlabel('Real')
ax1.set_ylabel('Imaginary')
fig.colorbar(c1, ax=ax1)

# 绘制虚部
c2 = ax2.imshow(np.imag(W), extent=[-2, 2, -2, 2], cmap='plasma', origin='lower')
ax2.set_title('Imaginary Part of exp(z) - how2matplotlib.com')
ax2.set_xlabel('Real')
ax2.set_ylabel('Imaginary')
fig.colorbar(c2, ax=ax2)

plt.tight_layout()
plt.show()

在这个例子中，我们计算了复平面上的指数函数值，并分别绘制了它的实部和虚部。这种可视化可以帮助我们理解复数指数函数的周期性和增长特性。

结论

通过本文，我们详细探讨了如何使用Matplotlib在Python中绘制复数。我们涵盖了从基本的复平面表示到复杂的复变函数可视化等多个方面。这些可视化技术不仅可以帮助我们更好地理解复数的性质，还能在实际应用中提供直观的洞察。

复数的可视化在许多领域都有重要应用，如信号处理、电气工程、量子力学等。通过掌握这些绘图技巧，我们可以更有效地分析和展示涉及复数的数据和模型。

希望这篇文章能够帮助你更好地理解和应用复数的可视化技术。随着你对Matplotlib和复数理论的深入学习，你将能够创建更加复杂和有洞察力的可视化效果。