Matplotlib中检测和可视化异常点的全面指南

Matplotlib中检测和可视化异常点的全面指南

参考：Finding the outlier points from Matplotlib

在数据分析和可视化中，识别和处理异常点是一个非常重要的任务。异常点可能代表着数据中的错误、特殊情况或有趣的模式。Matplotlib作为Python中最流行的绘图库之一，提供了多种方法来检测和可视化异常点。本文将详细介绍如何使用Matplotlib来找出并展示数据集中的异常点。

1. 什么是异常点？

异常点，也称为离群点或离群值，是指在数据集中与其他数据点显著不同或偏离预期的数据点。这些点可能由于测量错误、数据录入错误、或者真实的异常现象而产生。识别异常点对于以下几个方面非常重要：

• 数据清洗：帮助识别和处理可能的错误数据。
• 模式发现：异常点可能揭示数据中的有趣模式或特殊情况。
• 模型性能：异常点可能对统计分析和机器学习模型的性能产生显著影响。

2. 使用Matplotlib检测异常点的基本方法

2.1 散点图可视化

散点图是最直观的方法之一，可以帮助我们快速识别可能的异常点。以下是一个简单的示例：

import matplotlib.pyplot as plt
import numpy as np

# 生成示例数据
np.random.seed(42)
x = np.random.normal(0, 1, 100)
y = np.random.normal(0, 1, 100)

# 添加一些异常点
x = np.append(x, [3, -3, 3])
y = np.append(y, [3, 3, -3])

# 创建散点图
plt.figure(figsize=(10, 6))
plt.scatter(x, y, alpha=0.5)
plt.title('Scatter Plot for Outlier Detection - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.grid(True)
plt.show()

Output:

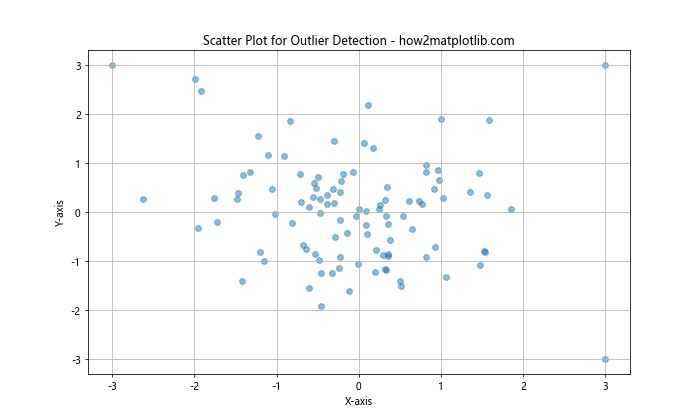
在这个示例中，我们生成了一组正态分布的数据点，并添加了三个明显的异常点。通过散点图，我们可以直观地看到这些异常点与主要数据群的区别。

2.2 箱线图（Box Plot）

箱线图是另一种有效识别异常点的方法，特别适用于单变量数据。

import matplotlib.pyplot as plt
import numpy as np

# 生成示例数据
np.random.seed(42)
data = np.random.normal(0, 1, 100)

# 添加一些异常点
data = np.append(data, [5, -5, 6])

# 创建箱线图
plt.figure(figsize=(10, 6))
plt.boxplot(data)
plt.title('Box Plot for Outlier Detection - how2matplotlib.com')
plt.ylabel('Values')
plt.grid(True)
plt.show()

Output:

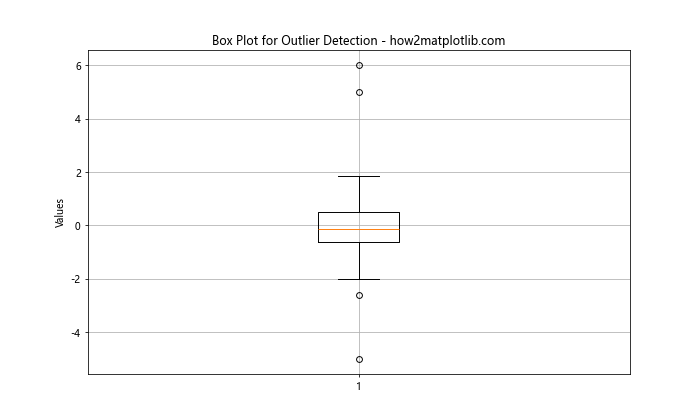
箱线图显示了数据的四分位数，以及超出1.5倍四分位距的点，这些点通常被视为潜在的异常点。

3. 高级异常点检测技术

3.1 Z-score方法

Z-score是一种统计方法，用于识别偏离平均值特定标准差倍数的数据点。

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats

# 生成示例数据
np.random.seed(42)
data = np.random.normal(0, 1, 100)
data = np.append(data, [5, -5, 6])  # 添加异常点

# 计算Z-score
z_scores = np.abs(stats.zscore(data))

# 设置阈值（通常使用3）
threshold = 3

# 找出异常点
outliers = data[z_scores > threshold]

# 绘制散点图
plt.figure(figsize=(10, 6))
plt.scatter(range(len(data)), data, c='b', label='Normal')
plt.scatter(np.where(z_scores > threshold)[0], outliers, c='r', label='Outlier')
plt.title('Z-score Outlier Detection - how2matplotlib.com')
plt.xlabel('Index')
plt.ylabel('Value')
plt.legend()
plt.grid(True)
plt.show()

Output:

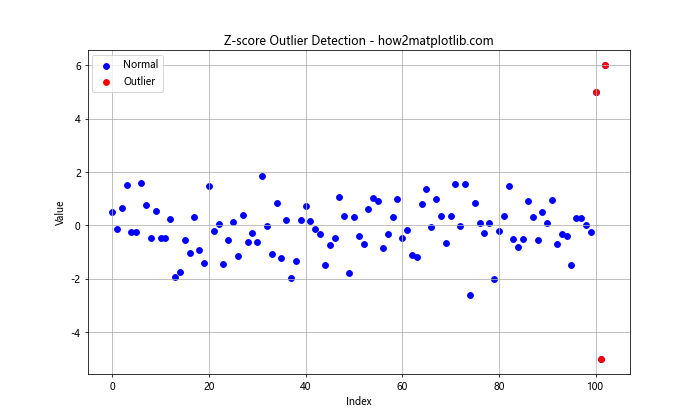
这个示例使用Z-score方法识别异常点，并在散点图中用不同颜色标记出来。

3.2 IQR（四分位距）方法

IQR方法使用四分位数来定义异常点的范围。

import matplotlib.pyplot as plt
import numpy as np

# 生成示例数据
np.random.seed(42)
data = np.random.normal(0, 1, 100)
data = np.append(data, [5, -5, 6])  # 添加异常点

# 计算Q1, Q3和IQR
Q1 = np.percentile(data, 25)
Q3 = np.percentile(data, 75)
IQR = Q3 - Q1

# 定义异常点范围
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR

# 找出异常点
outliers = data[(data < lower_bound) | (data > upper_bound)]

# 绘制散点图
plt.figure(figsize=(10, 6))
plt.scatter(range(len(data)), data, c='b', label='Normal')
plt.scatter(np.where((data < lower_bound) | (data > upper_bound))[0], outliers, c='r', label='Outlier')
plt.axhline(y=lower_bound, color='g', linestyle='--', label='Lower bound')
plt.axhline(y=upper_bound, color='g', linestyle='--', label='Upper bound')
plt.title('IQR Outlier Detection - how2matplotlib.com')
plt.xlabel('Index')
plt.ylabel('Value')
plt.legend()
plt.grid(True)
plt.show()

Output:

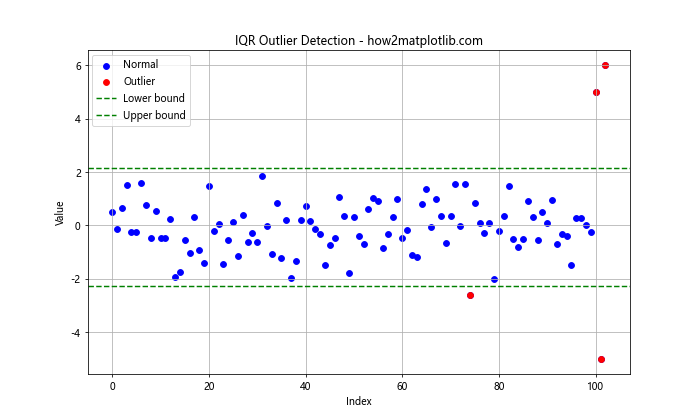
这个示例使用IQR方法来识别异常点，并在图中标记出异常点和边界线。

4. 多维数据的异常点检测

对于多维数据，我们可以使用更复杂的技术来检测异常点。

4.1 马氏距离（Mahalanobis Distance）

马氏距离考虑了数据的协方差结构，适用于多维数据的异常点检测。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import chi2

def mahalanobis(x, data):
    covariance_matrix = np.cov(data, rowvar=False)
    inv_covariance_matrix = np.linalg.inv(covariance_matrix)
    diff = x - np.mean(data, axis=0)
    return np.sqrt(diff.dot(inv_covariance_matrix).dot(diff.T))

# 生成示例数据
np.random.seed(42)
n_samples, n_features = 100, 2
data = np.random.multivariate_normal(mean=[0, 0], cov=[[1, 0.5], [0.5, 1]], size=n_samples)

# 添加异常点
data = np.vstack([data, [[3, 3], [-3, 3], [3, -3]]])

# 计算马氏距离
mahalanobis_distances = [mahalanobis(x, data) for x in data]

# 设置阈值（使用卡方分布的95%分位数）
threshold = np.sqrt(chi2.ppf(0.95, df=n_features))

# 找出异常点
outliers = data[np.array(mahalanobis_distances) > threshold]

# 绘制散点图
plt.figure(figsize=(10, 6))
plt.scatter(data[:, 0], data[:, 1], c='b', label='Normal')
plt.scatter(outliers[:, 0], outliers[:, 1], c='r', label='Outlier')
plt.title('Mahalanobis Distance Outlier Detection - how2matplotlib.com')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid(True)
plt.show()

Output:

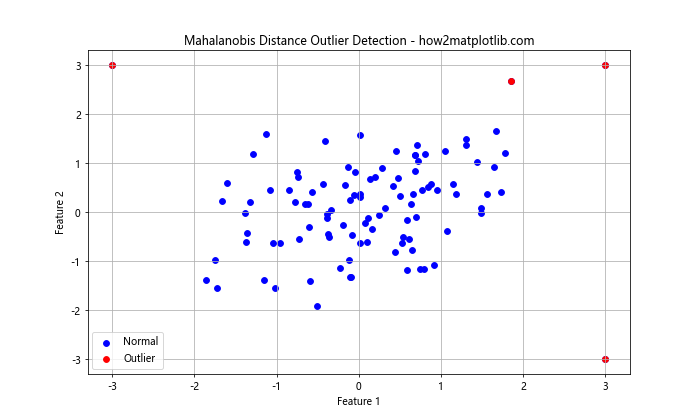
这个示例使用马氏距离来检测二维数据中的异常点。

4.2 局部异常因子（Local Outlier Factor, LOF）

LOF是一种基于密度的异常点检测方法，特别适用于具有不同密度区域的数据集。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.neighbors import LocalOutlierFactor

# 生成示例数据
np.random.seed(42)
X = np.random.normal(0, 1, (100, 2))
X = np.vstack([X, [[3, 3], [-3, 3], [3, -3]]])  # 添加异常点

# 使用LOF检测异常点
lof = LocalOutlierFactor(n_neighbors=20, contamination=0.1)
y_pred = lof.fit_predict(X)

# 绘制散点图
plt.figure(figsize=(10, 6))
plt.scatter(X[y_pred == 1, 0], X[y_pred == 1, 1], c='b', label='Normal')
plt.scatter(X[y_pred == -1, 0], X[y_pred == -1, 1], c='r', label='Outlier')
plt.title('Local Outlier Factor (LOF) Detection - how2matplotlib.com')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid(True)
plt.show()

Output:

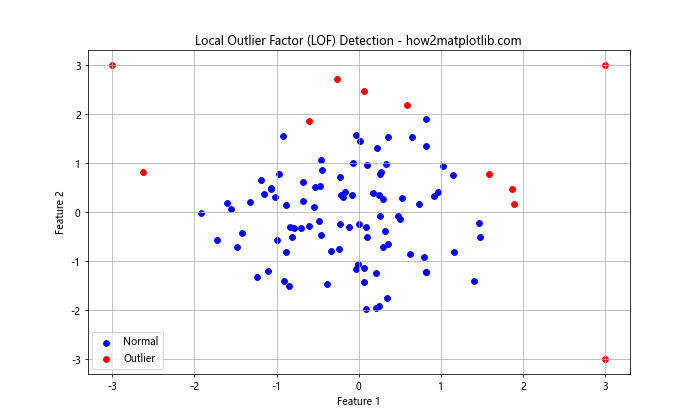
这个示例使用scikit-learn库中的LocalOutlierFactor来检测异常点。

5. 时间序列数据中的异常点检测

对于时间序列数据，我们可以使用移动平均线或指数加权移动平均线来检测异常点。

5.1 移动平均线方法

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

# 生成示例时间序列数据
np.random.seed(42)
dates = pd.date_range(start='2023-01-01', periods=100)
values = np.random.normal(0, 1, 100)
values[50] = 5  # 添加一个异常点

# 创建DataFrame
df = pd.DataFrame({'date': dates, 'value': values})
df.set_index('date', inplace=True)

# 计算移动平均线
window_size = 10
df['MA'] = df['value'].rolling(window=window_size).mean()

# 计算标准差
df['std'] = df['value'].rolling(window=window_size).std()

# 定义异常点
df['is_outlier'] = (df['value'] > df['MA'] + 2*df['std']) | (df['value'] < df['MA'] - 2*df['std'])

# 绘制图形
plt.figure(figsize=(12, 6))
plt.plot(df.index, df['value'], label='Original')
plt.plot(df.index, df['MA'], label='Moving Average')
plt.fill_between(df.index, df['MA'] - 2*df['std'], df['MA'] + 2*df['std'], alpha=0.2, label='2 Std Dev Range')
plt.scatter(df[df['is_outlier']].index, df[df['is_outlier']]['value'], color='red', label='Outlier')
plt.title('Time Series Outlier Detection - how2matplotlib.com')
plt.xlabel('Date')
plt.ylabel('Value')
plt.legend()
plt.grid(True)
plt.show()

Output:

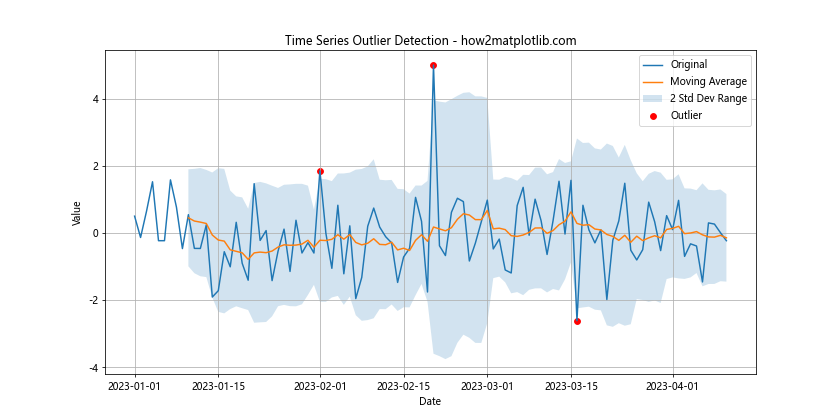
这个示例使用移动平均线和标准差来检测时间序列数据中的异常点。

5.2 季节性分解方法

对于具有季节性的时间序列数据，我们可以使用季节性分解来检测异常点。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from statsmodels.tsa.seasonal import seasonal_decompose

# 生成示例季节性时间序列数据
np.random.seed(42)
dates = pd.date_range(start='2023-01-01', periods=365)
trend = np.linspace(0, 10, 365)
seasonal = 5 * np.sin(np.linspace(0, 2*np.pi, 365))
noise = np.random.normal(0, 1, 365)
values = trend + seasonal + noise
values[180] = 25  # 添加一个异常点

# 创建DataFrame
df = pd.DataFrame({'date': dates, 'value': values})
df.set_index('date', inplace=True)

# 季节性分解
result = seasonal_decompose(df['value'], model='additive', period=30)

# 计算残差
residual = result.resid

# 定义异常点
threshold = 3 * np.std(residual.dropna())
df['is_outlier'] = np.abs(residual) > threshold

# 绘制图形
fig, (ax1, ax2, ax3, ax4) = plt.subplots(4, 1, figsize=(12, 16))

ax1.plot(df.index, df['value'])
ax1.set_title('Original Time Series - how2matplotlib.com')

ax2.plot(result.trend)
ax2.set_title('Trend')

ax3.plot(result.seasonal)
ax3.set_title('Seasonal')

ax4.plot(residual)
ax4.scatter(df[df['is_outlier']].index, residual[df['is_outlier']], color='red')
ax4.set_title('Residual and Outliers')

plt.tight_layout()
plt.show()

Output:

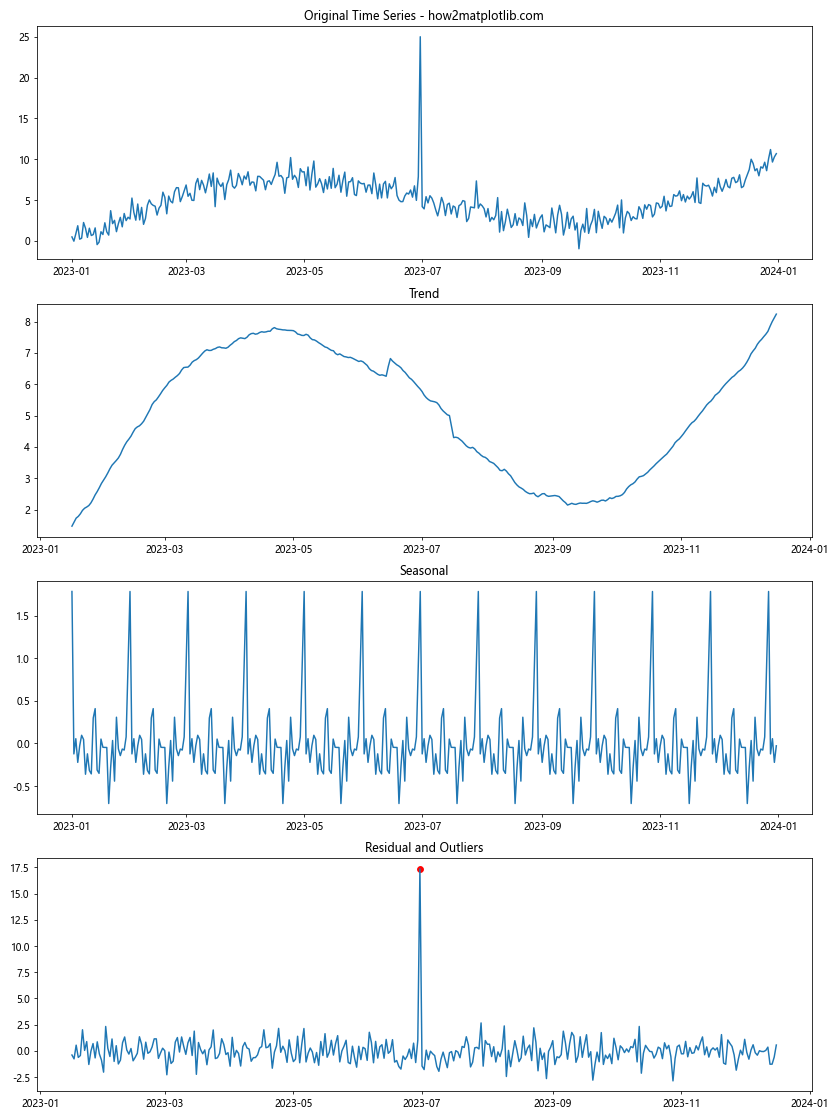
这个示例使用季节性分解方法来检测具有季节性的时间序列数据中的异常点。

6. 异常点检测的可视化技巧

6.1 使用颜色和形状突出显示异常点

import matplotlib.pyplot as plt
import numpy as np

# 生成示例数据
np.random.seed(42)
x = np.random.normal(0, 1, 100)
y = np.random.normal(0, 1, 100)

# 添加一些异常点
x = np.继续上文：

append(x, [3, -3, 3])
y = np.append(y, [3, 3, -3])

# 创建散点图
plt.figure(figsize=(10, 6))
plt.scatter(x[:-3], y[:-3], alpha=0.5, label='Normal')
plt.scatter(x[-3:], y[-3:], color='red', marker='*', s=200, label='Outlier')
plt.title('Highlighting Outliers - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.grid(True)
plt.show()

在这个示例中，我们使用不同的颜色（红色）和形状（星形）来突出显示异常点，使它们在视觉上更加明显。

6.2 使用注释标记异常点

import matplotlib.pyplot as plt
import numpy as np

# 生成示例数据
np.random.seed(42)
x = np.random.normal(0, 1, 100)
y = np.random.normal(0, 1, 100)

# 添加一些异常点
outliers_x = [3, -3, 3]
outliers_y = [3, 3, -3]
x = np.append(x, outliers_x)
y = np.append(y, outliers_y)

# 创建散点图
plt.figure(figsize=(10, 6))
plt.scatter(x, y, alpha=0.5)

# 添加注释
for i, (ox, oy) in enumerate(zip(outliers_x, outliers_y)):
    plt.annotate(f'Outlier {i+1}', (ox, oy), xytext=(5, 5), 
                 textcoords='offset points', ha='left', va='bottom',
                 bbox=dict(boxstyle='round,pad=0.5', fc='yellow', alpha=0.5),
                 arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0'))

plt.title('Annotating Outliers - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.grid(True)
plt.show()

Output:

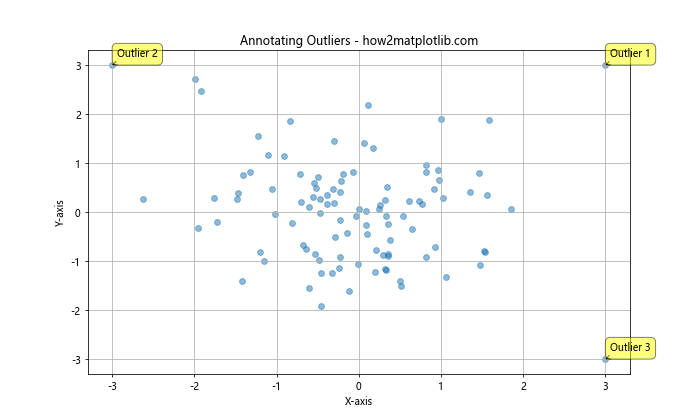
这个示例展示了如何使用注释来标记和描述异常点，使它们更容易被识别和理解。

6.3 使用热力图可视化多维数据中的异常点

对于多维数据，热力图可以帮助我们识别异常模式。

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

# 生成示例数据
np.random.seed(42)
data = np.random.normal(0, 1, (20, 5))
data[5, :] = np.random.normal(3, 1, 5)  # 添加一个异常样本

# 创建热力图
plt.figure(figsize=(10, 8))
sns.heatmap(data, cmap='YlOrRd', annot=True, fmt='.2f')
plt.title('Heatmap for Outlier Detection - how2matplotlib.com')
plt.xlabel('Features')
plt.ylabel('Samples')
plt.show()

Output:

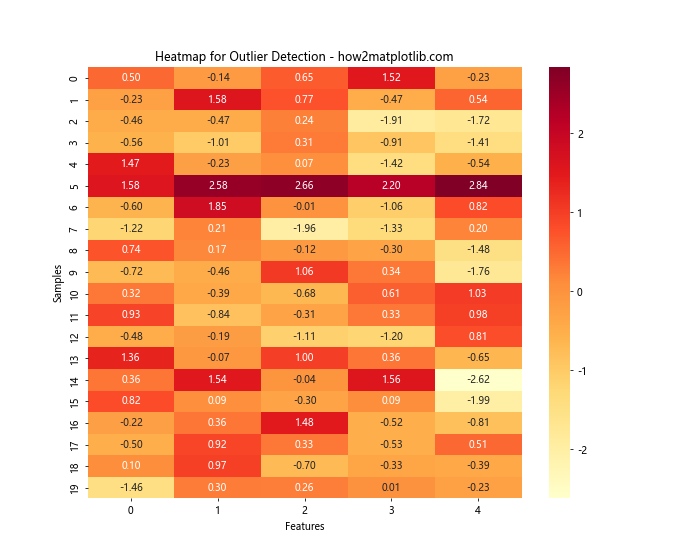
这个热力图可以帮助我们快速识别出与其他样本显著不同的行或列，这些可能代表异常点或异常模式。

7. 处理异常点的策略

识别异常点后，我们需要决定如何处理它们。以下是一些常见的策略：

7.1 移除异常点

在某些情况下，我们可能选择完全移除异常点。这里是一个示例，展示了如何移除异常点并比较结果：

import matplotlib.pyplot as plt
import numpy as np

# 生成示例数据
np.random.seed(42)
x = np.random.normal(0, 1, 100)
y = 2 * x + np.random.normal(0, 1, 100)

# 添加一些异常点
x = np.append(x, [3, -3, 3])
y = np.append(y, [10, -10, -10])

# 定义异常点
outliers = (np.abs(x) > 2.5) | (np.abs(y) > 5)

# 创建两个子图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

# 原始数据
ax1.scatter(x, y)
ax1.set_title('Original Data - how2matplotlib.com')
ax1.set_xlabel('X-axis')
ax1.set_ylabel('Y-axis')

# 移除异常点后的数据
ax2.scatter(x[~outliers], y[~outliers])
ax2.set_title('Data After Removing Outliers - how2matplotlib.com')
ax2.set_xlabel('X-axis')
ax2.set_ylabel('Y-axis')

plt.tight_layout()
plt.show()

Output:

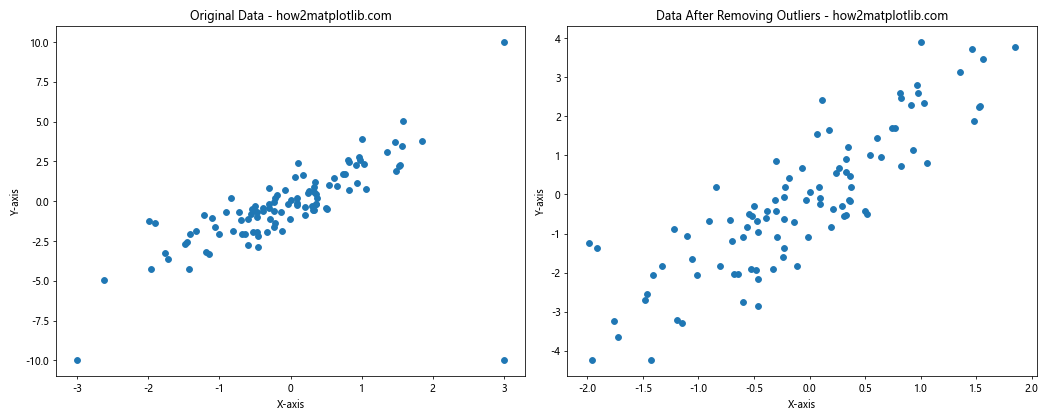
这个示例展示了移除异常点前后的数据分布对比。

7.2 对异常点进行变换

有时，我们可能选择对异常点进行变换而不是完全移除它们。例如，我们可以使用对数变换来减小极端值的影响：

import matplotlib.pyplot as plt
import numpy as np

# 生成示例数据
np.random.seed(42)
data = np.random.lognormal(0, 1, 1000)

# 创建两个子图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

# 原始数据
ax1.hist(data, bins=50)
ax1.set_title('Original Data Distribution - how2matplotlib.com')
ax1.set_xlabel('Value')
ax1.set_ylabel('Frequency')

# 对数变换后的数据
ax2.hist(np.log(data), bins=50)
ax2.set_title('Log-transformed Data Distribution - how2matplotlib.com')
ax2.set_xlabel('Log(Value)')
ax2.set_ylabel('Frequency')

plt.tight_layout()
plt.show()

Output:

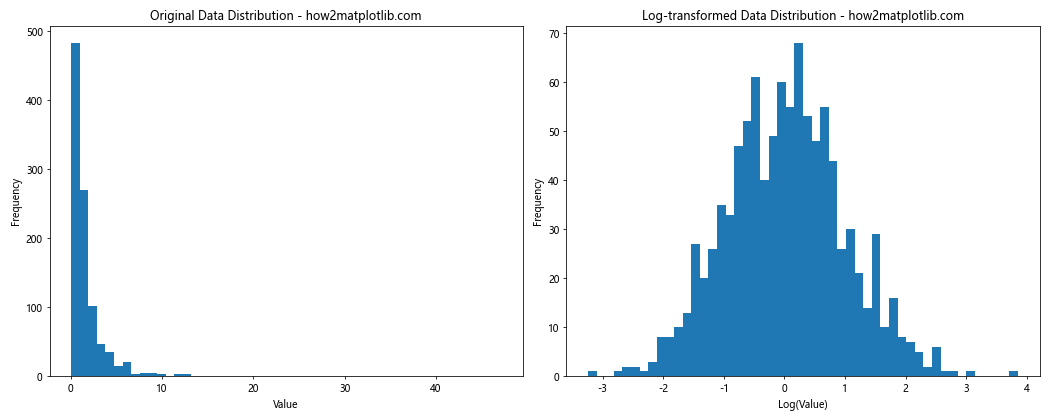
这个示例展示了对数变换如何改变数据分布，使得异常点的影响减小。

7.3 使用稳健统计方法

另一种处理异常点的方法是使用稳健统计方法，这些方法对异常点不敏感。例如，我们可以使用中位数而不是平均值来表示中心趋势：

import matplotlib.pyplot as plt
import numpy as np

# 生成示例数据
np.random.seed(42)
data = np.random.normal(0, 1, 100)
data = np.append(data, [10, -10, 15])  # 添加异常点

# 计算平均值和中位数
mean = np.mean(data)
median = np.median(data)

# 创建直方图
plt.figure(figsize=(10, 6))
plt.hist(data, bins=30, alpha=0.7)
plt.axvline(mean, color='r', linestyle='dashed', linewidth=2, label=f'Mean: {mean:.2f}')
plt.axvline(median, color='g', linestyle='dashed', linewidth=2, label=f'Median: {median:.2f}')
plt.title('Comparison of Mean and Median - how2matplotlib.com')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.legend()
plt.show()

Output:

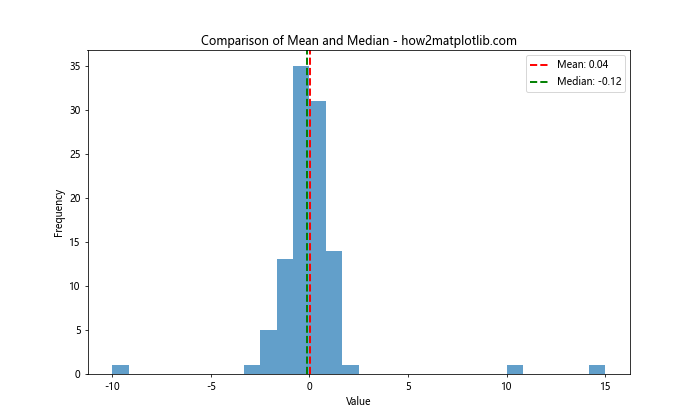
这个示例展示了在存在异常点的情况下，中位数如何提供更稳健的中心趋势估计。

8. 结合机器学习的异常点检测

在某些情况下，我们可能需要使用更复杂的机器学习方法来检测异常点，特别是在处理高维数据或复杂模式时。

8.1 使用隔离森林（Isolation Forest）

隔离森林是一种基于树的异常点检测算法，特别适用于高维数据。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.ensemble import IsolationForest

# 生成示例数据
np.random.seed(42)
X = np.random.normal(0, 1, (100, 2))
X = np.vstack([X, [[3, 3], [-3, 3], [3, -3]]])  # 添加异常点

# 使用隔离森林检测异常点
clf = IsolationForest(contamination=0.1, random_state=42)
y_pred = clf.fit_predict(X)

# 绘制散点图
plt.figure(figsize=(10, 6))
plt.scatter(X[y_pred == 1, 0], X[y_pred == 1, 1], c='b', label='Normal')
plt.scatter(X[y_pred == -1, 0], X[y_pred == -1, 1], c='r', label='Outlier')
plt.title('Isolation Forest Outlier Detection - how2matplotlib.com')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid(True)
plt.show()

Output:

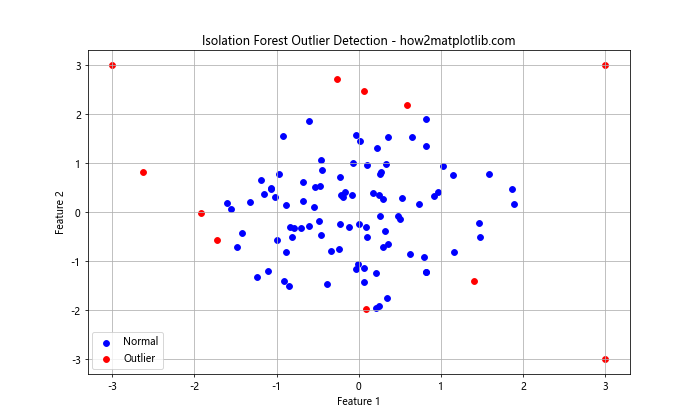
这个示例展示了如何使用隔离森林算法来检测二维数据中的异常点。

8.2 使用One-Class SVM

One-Class SVM是另一种常用的异常点检测算法，特别适用于复杂的数据分布。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.svm import OneClassSVM

# 生成示例数据
np.random.seed(42)
X = np.random.normal(0, 1, (100, 2))
X = np.vstack([X, [[3, 3], [-3, 3], [3, -3]]])  # 添加异常点

# 使用One-Class SVM检测异常点
clf = OneClassSVM(kernel='rbf', nu=0.1)
y_pred = clf.fit_predict(X)

# 绘制散点图和决策边界
xx, yy = np.meshgrid(np.linspace(-4, 4, 50), np.linspace(-4, 4, 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.figure(figsize=(10, 6))
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu)
plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='darkred')
plt.scatter(X[y_pred == 1, 0], X[y_pred == 1, 1], c='b', label='Normal')
plt.scatter(X[y_pred == -1, 0], X[y_pred == -1, 1], c='r', label='Outlier')
plt.title('One-Class SVM Outlier Detection - how2matplotlib.com')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()

Output:

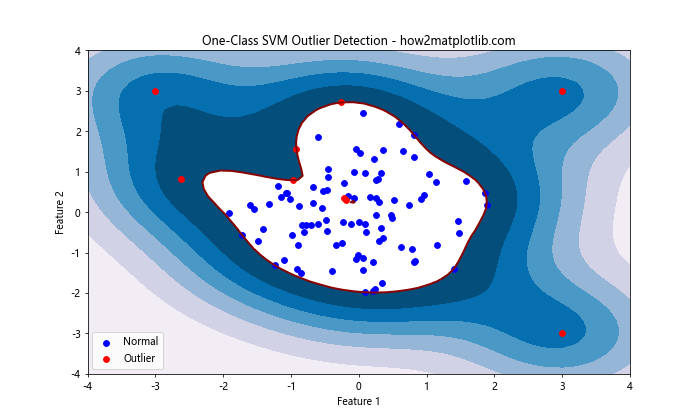
这个示例展示了如何使用One-Class SVM来检测异常点，并可视化决策边界。

9. 总结

在本文中，我们详细探讨了使用Matplotlib检测和可视化异常点的多种方法。从基本的散点图和箱线图，到高级的统计方法如Z-score和IQR，再到机器学习算法如隔离森林和One-Class SVM，我们涵盖了广泛的技术。

关键点总结：

1. 异常点检测是数据分析和可视化中的重要任务。
2. Matplotlib提供了多种工具来可视化和识别异常点。
3. 对于不同类型的数据（单变量、多变量、时间序列），我们需要采用不同的方法。
4. 可视化技巧，如使用不同的颜色、形状和注释，可以帮助更好地展示异常点。
5. 处理异常点的策略包括移除、变换和使用稳健统计方法。
6. 机器学习算法可以用于更复杂的异常点检测任务。

在实际应用中，选择合适的异常点检测和可视化方法取决于具体的数据特征和分析目标。通过结合多种方法和技术，我们可以更全面、准确地识别和理解数据中的异常点，从而做出更informed的决策和洞察。