Java 检查根据给定条件构建的数组图是否包含循环

介绍

在图论中，确定根据数组构建的图是否满足一定条件并包含循环是一项非常重要的任务。图是一种表示事物之间连接关系的想象方式。它在许多地方使用，如计算机网络和社交网络。本文讨论了图构建的条件、BFS和DFS算法，以及如何逐步识别无向图中的循环。

数组表示的图

图论中的数组表示方法将顶点和边存储在数组中，使它们易于处理和在算法中使用。从空图开始，根据数组中的信息逐个添加顶点和边是进一步探索的基础，如循环检测，这对于了解图的连接方式和是否存在循环很重要。

图构建的条件

给定条件的解释

• 图是从一个数组构建的，其中数组表示一组顶点及其连接或边。

• 数组的每个元素对应图中的一个顶点。

• 数组中每个元素的值表示它所连接的顶点的索引（相邻顶点）。

• 数组的索引代表顶点本身，其对应的值表示它所连接的顶点。

验证图构建的条件

• 在构建图之前，检查数组是否有效并满足所需条件。

• 确保数组不为空，并至少包含一个元素以创建一个顶点。

• 验证数组仅包含非负整数，因为负值或无效数据不能表示有效的顶点或边。

• 确保数组索引在适当的范围内。它们应从0到n-1，其中n是图中顶点的总数。

• 确认数组中的值（连接）也在0到n-1的有效范围内，确保它们与现有顶点对应。

• 检查是否存在重复连接或自循环，因为它们违反了有效图的条件。

• 验证没有缺失的连接，即所有顶点都连通以形成完整的图或连接组件。

DFS和BFS算法

• 深度优先搜索（DFS）用于通过尽可能深入每个分支，然后返回，探索图的顶点和边。

伪代码

procedure DFS(graph, start_vertex, visited)
   if start_vertex is not in visited:
      mark start_vertex as visited
      process start_vertex (e.g., check for cycles)
      for each neighbor in graph[start_vertex]:
      if neighbor is not in visited:
      DFS(graph, neighbor, visited)
   end if
end procedure
    pocedure DFS_Traversal(graph)
    visited = empty set
      for each vertex in graph:
      if vertex is not in visited:
         DFS(graph, vertex, visited)
   end for
end procedure

• 广度优先搜索（BFS）是一种图遍历算法，它一次遍历图的所有顶点的一个级别。这使得它成为查找图中循环的一种很好的方法。

伪代码

procedure BFS(graph, start_vertex):
   create an empty queue Q
   create a set visited to keep track of visited vertices

   enqueue start_vertex into Q
   add start_vertex to visited set

   while Q is not empty:
      current_vertex = dequeue from Q
      for each neighbor_vertex of current_vertex:
         if neighbor_vertex is not in visited set:
            enqueue neighbor_vertex into Q
            add neighbor_vertex to visited set
      else:
         // A cycle is detected, return true
         return true
      // No cycle found, return false
      return false

复杂性

• 时间复杂度

BFS和DFS的时间复杂度均为O(V + E)，其中V是顶点的数量，E是边的数量。

• 空间复杂度

BFS和DFS的空间复杂度均为O(V)。

逐步循环检测过程

让我们考虑一个带有图的示例

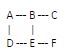
• 从一个空集开始，以监视访问过的顶点

Visited set: {}

• 选择任意一个顶点作为循环检测过程的起始点。让我们选择顶点 A。

Visited set: {A}
Current Vertex: A

• 检查当前顶点(A)的相邻顶点。在这个例子中，A的邻居是B和D。将它们添加到已访问集合，并将A标识为它们的父节点。

Visited set: {A, B, D}
Current Vertex: A
Parent of B: A
Parent of D: A

• B是访问集合中的下一个访问顶点。

Visited set: {A, B, D}
Current Vertex: B
Parent of B: A

• 发现B的周围环境。B的直接邻居是A，C和E。A已经在访问过的顶点集合中，但它不是B的父节点，因此它不构成一个循环。

Visited set: {A, B, D, C, E}
Current Vertex: B

• 继续前往下一个已访问的顶点，即D。

Visited set: {A, B, D, C, E}
Current Vertex: D
Parent of D: A

• 发现D的熟人。A和E是D最亲密的邻居。由于A已经包含在已访问集合中并且是D的父节点，所以D与其父节点之间必定存在一条边(D -> A)，这说明图中存在一个循环。

Cycle detected! There is an edge (D -> A) forming a cycle

该过程到此结束，并且我们使用BFS成功检测出了图中的循环，即(A->B->E->D->A)。

结论

总之，对于许多应用来说，能够根据给定的参数从数组构建的图中找到循环是很重要的。不论你使用DFS还是BFS，该过程有助于找到可能的循环并解决涉及网络、电路和关系的现实世界问题。良好的循环检测可以改善算法的速度，并确保数据的正确性。