C++ 最大化给定半径的半圆的一个值

对于标题中嵌入的问题”最大化给定半径的半圆的一个值”你理解的是什么？

标题”最大化给定半径的半圆的一个值”听起来不清楚，对吧？让我们在下面的文章中讨论它的含义：

根据标题，如果我们有一个半径为R的半圆，我们需要找到表达式F = PS^2 + PQ的最大值，其中P是半圆周上的一个点，而PQ和PS是连接P到直径的两段线段。还是感到困惑吗？看一下下面的图表，然后试着理解。

C++ 最大化给定半径的半圆的一个值

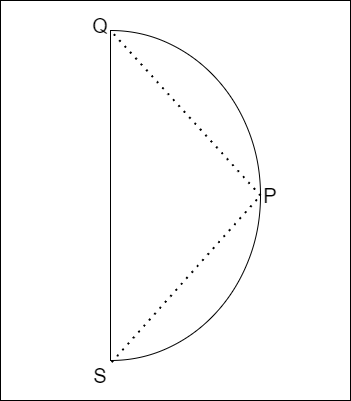
现在你能理解问题了吗？很好，现在让我们转到我们需要实施的逻辑。

如果你仔细观察图表，你会注意到三角形PQS无论点P在圆周上的位置如何，它总是一个直角三角形。

所以，由于PQS是直角的，我们可以使用勾股定理来关联这个三角形的边，如下所示：

QS^2 = PQ^2 + PS^2 (h^2= b^2+p^2)

由于QS是半圆的直径，我们知道QS = 2R。将这个值代入上述等式，我们得到：

4R^2 = PQ^2 + PS^2

我们可以将这个等式重新排列如下：PS^2 = 4R^2 − PQ^2
我们可以将这个表达式代入F的表达式中，得到：F = 4R^2 − PQ^2 + PQ

现在进入下一步，你可能已经了解了关于最大值和最小值的知识。为了找到F的最大值，我们可以使用最大值和最小值的概念。我们将F对PQ求导，并将导数设为零，以找到F的临界点。

dF/dPQ = −2PQ + 1

将导数设为零，我们得到：−2PQ + 1 = 0
解出PQ，我们得到：PQ = ½
将这个PQ的值代入F的表达式中，我们得到：

F = 4R^2 + 1/4

因此，F的最大值是4R^2 + 1/4，当PQ = 1/2时达到。这个最大值与点P在半圆周上的位置无关。

方法

在讨论了解决问题所需的逻辑之后，让我们讨论将上述逻辑转换为可工作代码的逐步方法。

我们将半圆的半径作为输入。
现在，我们将使用上面得出的公式计算最大值（4R^2 + 1/4）。
现在，我们将最大值打印到控制台。

C++代码实现

理论太多？现在我们有了逻辑和方法，让我们将它们转化为可工作的代码。下面是根据给定半径最大化半圆值的C++代码实现。

示例

#include <iostream>
#include <cmath>
using namespace std;double findMaxF(double R) {    
   double F = 4 * R * R + 1.0 / 4.0;    
   return F;
}
int main() {    
   double R = 3.5;    
   double maxF = findMaxF(R);    
   cout << "The maximum value of F is: " << maxF << endl;    
   return 0;
}