C++ 使用随机枢轴的快速排序
快速排序是一种分治算法。在此算法中,我们选择一个枢轴元素,然后围绕该枢轴元素对数组进行划分。两个分区使得一个部分包含所有小于枢轴元素的元素,另一个部分包含所有大于枢轴元素的元素。类似地,每个部分都会围绕该部分中选择的枢轴进行进一步划分,直到达到单个元素为止。
选择枢轴
可以按如下方式在数组中选择枢轴 −
- 随机选择枢轴。
-
将最右侧或最左侧的元素作为枢轴。
-
将中间元素作为枢轴。
在本文中,我们将使用第一种方法选择枢轴并实现快速排序算法。
问题陈述
给定一个数组。使用使用随机枢轴的快速排序算法对数组进行排序。
示例示例1
Input: [3, 1, 7, 2, 10]
Output: [1, 2, 3, 7, 10]
解释 − 假设3被选择为随机的枢纽,将其与10交换,并将3设置为枢纽,使用3作为枢纽来对数组进行划分。在第一次划分后,数组变为[1, 2, 3, 7, 10],其中3在其排序位置上。然后分别对3左边和右边的子数组调用函数来对剩余的数组进行排序。
示例2
Input: [11, 32, 7, 90, 18, 34]
Output: [7, 11, 18, 32, 34, 90]
伪代码
Swap() 的伪代码
procedure swap (*a, *b)
temp = *a
*a = *b
*b = temp
end procedure
pickRandom()的伪代码
procedure pickRandom (arr[], start, end)
num = Random number between start and end
swap arr[num] and arr[end]
end procedure
partition() 的伪代码
procedure partition (arr[], start, end)
pickRandom (arr, start, end)
pivot = arr[end]
i = start
for k = start to end - 1
if arr[k] <= pivot
swap arr[k] and arr[i]
i = i + 1
end if
end for
swap arr[i] and arr[end]
return i
end procedure
伪代码快速排序()
procedure quickSort (arr[], start, end)
if start < end
p = pickRandom (arr[], start, end)
quickSort (arr[], start, p-1)
quickSort (arr[], p+1, end)
end if
end procedure
工作中
让我们取一个未排序的数组,并从开始到结束调用staaquickSort()函数。

从pickRandom()函数开始,
令num = start和end之间的随机数 = 2
交换arr[1]和arr[end],我们得到以下数组,

在调用partition()函数时,
Pivot = arr[end] = 23
由于pivot在末尾,所以算法从开始向末尾移动。在一个循环中将k从start到end – 1,并且i = start
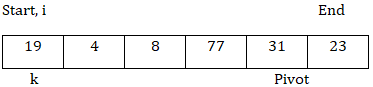
现在,arr[k] < arr[pivot],所以交换arr[k]和arr[i],然后i = i + 1。
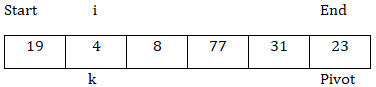
现在,arr[k] < arr[pivot],所以交换arr[k]和arr[i],然后i = i + 1。
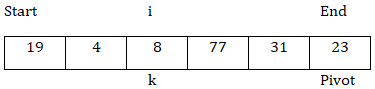
现在,arr[k] < arr[pivot],所以交换arr[k]和arr[i],然后i = i + 1。
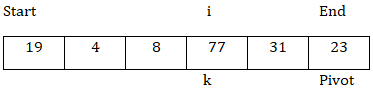
现在,arr[k] > arr[pivot],所以k向前移动。
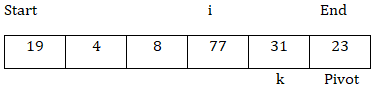
现在,arr[k] > arr[pivot]并且循环结束。
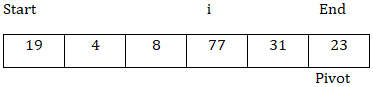
循环结束后,交换arr[i]和arr[pivot]。
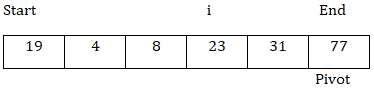
返回i = 3。
因此,下一个quickSort()在从开始到i-1的数组上调用,然后在i+1到末尾的数组上调用。
示例:C++实现
在下面的程序中,为了使用随机选取枢轴进行快速排序,我们首先选择数组的一个随机索引。然后将随机索引上的数字与数组的最后一个元素交换。然后选择最后一个元素作为枢轴。然后围绕这个枢轴对数组进行划分,并在划分的数组上递归调用quickSort,直到每个子数组中只剩下一个元素。
#include <bits/stdc++.h>
using namespace std;
// function to swap values of two variables
void swap(int *x, int *y){
int t = *x;
*x = *y;
*y = t;
}
// This function picks a random index between start and end and swaps the value at that index to the value at end index.
void pickRandom(int arr[], int start, int end){
int num = start + rand() % (end - start + 1);
swap(arr[num], arr[end]);
}
// This function calls the pickRandom() function and then partitions the array into two subarrays
int partition(int arr[], int start, int end){
pickRandom(arr, start, end);
// End element is chosen as pivot
int pivot = arr[end];
int i = start;
for (int k = start; k < end; k++){
if (arr[k] <= pivot){
swap(arr[k], arr[i]);
i++;
}
}
swap(arr[i], arr[end]);
// The array is divided into two sub-parts with the left part having all the elements smaller than the pivot and right part having elements bigger than the pivot.
return i;
}
void quickSort(int arr[], int start, int end){
if (start < end){
// p is the point of partition
int p = partition(arr, start, end);
// Calling quicksort on left subarray
quickSort(arr, start, p - 1);
// Calling quicksort on right subarray
quickSort(arr, p + 1, end);
}
}
int main(){
int arr[6] = {19, 4, 23, 77, 31, 8};
// Before Sorting
cout << "Array before sorting : ";
for (int i = 0; i < 6; i++){
cout << arr[i] << " ";
}
// Applying quick Sort
quickSort(arr, 0, 5);
// After Sorting
cout << "\nArray after sorting : ";
for (int i = 0; i < 6; i++){
cout << arr[i] << " ";
}
return 0;
}
输出
Array before sorting : 19 4 23 77 31 8
Array after sorting : 4 8 19 23 31 77
时间复杂度 – 最坏情况下的复杂度 = O(n2)
平均(预期)情况下的复杂度 = O(nlogn)。
空间复杂度 – 由于使用递归堆栈空间,复杂度为O(nlogn)。
结论
总之,使用快速排序和随机选择枢轴对数组进行排序可以通过O(nlogn)来改善平均或预期时间复杂度,但最坏情况下复杂度仍为O(n2)。
 极客笔记
极客笔记