C++ 程序矩阵行列式

矩阵行列式是线性代数中的重要概念，C++ 程序可以用来求解矩阵行列式。下面将介绍如何用 C++ 程序求解矩阵行列式的方法。

矩阵行列式的定义

矩阵行列式是一个函数，它把一个 n 乘 n 的矩阵映射到一个数。矩阵行列式可以通过递归定义来计算。

对于 1×1 的矩阵，其行列式就是该矩阵元素的值。

对于 2×2 的矩阵：

C++ 程序矩阵行列式

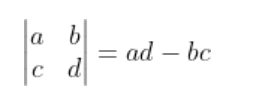
对于 n×n 的矩阵，其行列式可以用递归公式来计算：

C++ 程序矩阵行列式

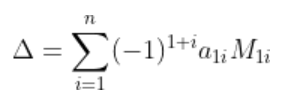
其中 M1i 是把第一行和第 i 列除去后剩余元素组成的 n-1×n-1 矩阵的行列式。

C++ 程序实现矩阵行列式的计算

在 C++ 程序中，可以使用二维数组来表示矩阵，使用递归函数来计算行列式。

下面是一个用 C++ 实现矩阵行列式计算的示例代码，代码中使用了递归函数来计算行列式：

#include <iostream>
using namespace std;

const int MAXN = 100;

int det(int a[MAXN][MAXN], int n) {
    int res = 0;
    if (n == 1) {
        return a[0][0];
    } else {
        for (int j = 0; j < n; j++) {
            int t[MAXN][MAXN];
            for (int i = 1; i < n; i++) {
                int k = 0;
                for (int p = 0; p < n; p++) {
                    if (p == j) {
                        continue;
                    }
                    t[i - 1][k++] = a[i][p];
                }
            }
            res += ((j % 2 == 1) ? -1 : 1) * a[0][j] * det(t, n - 1);
        }
    }
    return res;
}

int main() {
    int n;
    cin >> n; // 输入矩阵的大小
    int a[MAXN][MAXN];
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            cin >> a[i][j];
        }
    }

    cout << det(a, n) << endl; // 求解矩阵行列式并输出

    return 0;
}

上述代码中，函数 det 是递归计算矩阵行列式的函数。在函数中，如果矩阵大小为 1，则返回矩阵元素的值；否则对于每一个列 j 递归计算其剩余元素的行列式 t，然后按照行列式的计算公式计算得到整个矩阵的行列式。