计算机网络 错误纠正

错误纠正码用于在数据从发送方传输到接收方时检测和纠正错误。

错误纠正有两种处理方式：

• 向后错误纠正： 一旦发现错误，接收方会请求发送方重新传输整个数据单元。
• 向前错误纠正： 在这种情况下，接收方使用自动纠错码来自动纠正错误。

一个附加位可以检测错误，但不能纠正错误。

为了纠正错误，必须知道错误的确切位置。例如，如果我们想要计算一个单比特错误，错误纠正码将确定七位中的哪一位出错。为了实现这一点，我们需要添加一些额外的冗余位。

假设r是冗余位的数量，d是数据位的总数。可以使用以下公式计算冗余位r的数量：

2r>=d+r+1

根据上述公式计算r的值。例如，如果d的值为4，则满足上述关系的可能的最小值为3。

为了确定错误位的位置，R.W Hamming开发了一种称为Hamming code的技术，它可以应用于任意长度的数据单元，并使用数据单元和冗余单元之间的关系。

Hamming码

奇偶位： 将附加到二进制位的原始数据中，以便1的总数是偶数或奇数。

偶校验： 为了检查偶校验，如果1的总数是偶数，则奇偶校验位的值为0。如果1的总数是奇数次出现，则奇偶校验位的值为1。

奇校验： 为了检查奇校验，如果1的总数是偶数，则奇偶校验位的值为1。如果1的总数是奇数，则奇偶校验位的值为0。

Hamming码的算法：

• 将’d’位的信息添加到冗余位’r’以形成d+r。
• 为(d+r)位的每个位置分配一个十进制值。
• 将’r’位放置在位置1、2、…..2 k-1 。
• 在接收端，重新计算奇偶校验位。奇偶校验位的十进制值确定错误的位置。

错误位置与二进制数之间的关系。

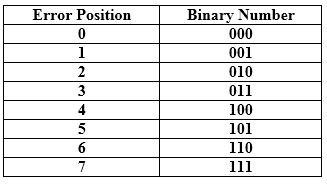
通过一个例子来理解海明码的概念:

假设原始数据是1010，需要发送。

Total number of data bits ‘d’ = 4
Number of redundant bits r : 2r >= d+r+1
2r>= 4+r+1
Therefore, the value of r is 3 that satisfies the above relation.
Total number of bits = d+r = 4+3 = 7;

确定冗余位的位置

冗余位的数量为3。这三个位被表示为r1, r2, r4。冗余位的位置是根据2的乘幂进行计算的。因此，它们对应的位置分别是 **1, 2 1 , 2 2 ** .

The position of r1 = 1
The position of r2 = 2
The position of r4 = 4

加入奇偶校验位的数据表示：

确定奇偶校验位

确定r1位

r1位通过对二进制表示中第一位为1的位置进行奇偶校验计算得出。

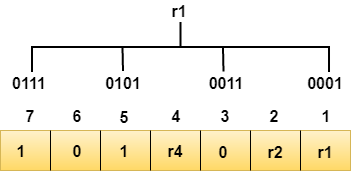
从上面的图中我们可以观察到，第一位中包含1的位位置是1、3、5、7。现在，在这些位位置上进行偶校验检查。在这些位位置上，与r1相对应的1的总数是 偶数 ，因此r1位的值为0。

确定r2位

通过对二进制表示中包含第二位的位位置进行奇偶校验，来计算r2位。

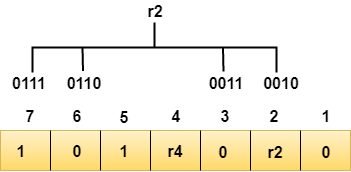
我们观察到从上面的图中，第二位上包含1的位位置有 2、3、6、7 。现在，我们在这些位位置上进行偶校验检查。在这些与r2相对应的位位置上1的总数是 奇数 ，因此，r2位的值为1。

确定r4位

通过对二进制表示中包含1的第三位的位位置进行奇偶校验检查来计算r4位。

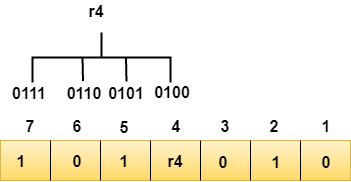
我们观察以上图表，发现第三位包含1的位数是 4, 5, 6, 7 。现在，我们在这些位数上执行偶校验检查。对应r4的这些位数上的1的总数是 偶数 ，因此r4位的值为 0 。

传输的数据如下所示:

假设第4个二进制位在接收端由0变为1，那么校验位将被重新计算。

R1位

r1位的位置分别为1、3、5、7。

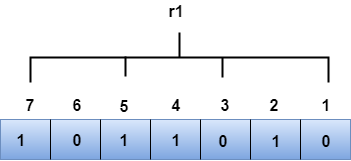
从上图中我们可以观察到r1的二进制表示为1100。现在，我们进行奇偶校验检查，出现在r1位上的1的总数是一个偶数。因此，r1的值是0。

R2位

r2位的位位置是2、3、6、7。

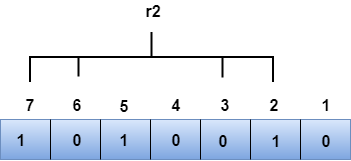
我们从上图中观察到，r2的二进制表示为1001。现在，我们进行偶数校验检查，r2位中出现的1的总数是偶数。因此，r2的值为0。

R4位

r4位的位位置为4,5,6,7。

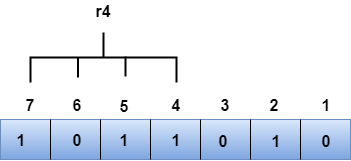
从上图中我们观察到，r4的二进制表示是1011。现在，我们进行偶校验检查，r4位中出现的1的总数是奇数。因此，r4的值是1。

• 冗余位（即r4r2r1）的二进制表示是100，对应的十进制值是4。因此，错误发生在第4位位置。位值必须从1改变为0以纠正错误。