在本章中,我们将了解 K-Means 聚类的概念,以及它是如何工作的,等等。
K-Means 聚类原理
我们将用一个常用的例子来解释原理。
T 恤大小问题
举个例子,有一家公司将向市场推出一种新型 T 恤。显然,他们必须制造不同尺寸的衣服,以满足各种身材的人。为此,公司收集了一份人的身高和体重的数据,并将其绘制成图表,如下所示:
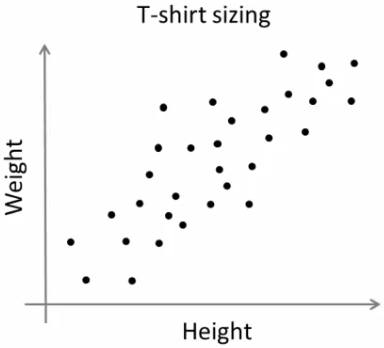
公司不能制作所有尺寸的 T 恤。相反,他们将人们划分为小巧、中等和高大,并且仅制造这 3 种尺寸的衣服,以满足所有人的需求。将人群分为 3 组这种事情可以用 K-Means 聚类算法来完成,并且算法能够给我们找出最合适的 3 个尺寸,让所有人满意。如果不行,公司可以将人们分成更多的组,可能是 5 组,或者其它。查看下图:
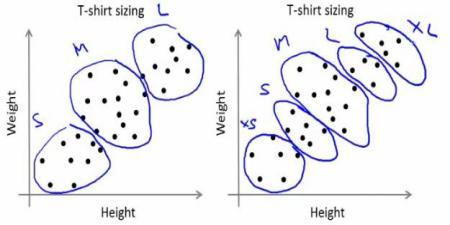
如何工作的?
该算法是一个迭代过程,我们将在图像的帮助下逐步解释它。
考虑如下的一组数据(你可以将其视为 T 恤问题)。我们需要将这些数据分成两组。
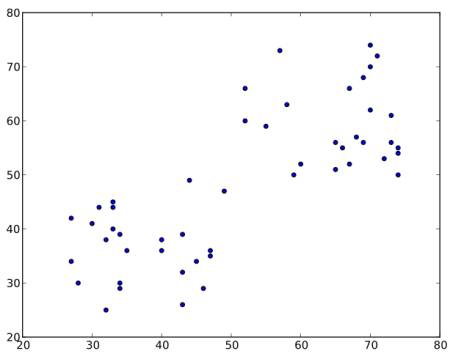
步骤一: 算法随机选择两个中心点 C1 和 C2(有时,任何两个数据都可以被选为中心点)。
步骤二: 计算从每个点到两个中心点的距离。如果测试数据更接近 C1,则该数据标记为’0’。如果它更接近 C2,则标记为’1’(如果有更多中心点,标记为’2’,’3’等)。
在这个例子中,我们用红色标记所有的’0’,用蓝色标记所有的’1’。在上述操作之后,我们得到了下图:
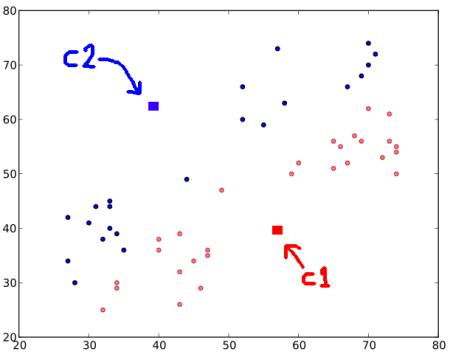
步骤三: 接下来,我们分别计算所有蓝点和红点的平均值,这将是我们的新中心点。将 C1 和 C2 移过去。(要记住,这个图像所显示的并不是真正的值,也不是真正的规模,它仅用于演示)。
再来一次,使用新的中心点执行步骤二,并将数据标记为’0’和’1’。
然后我们得到了如下结果:
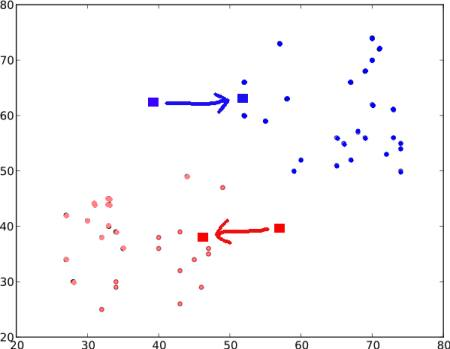
现在,迭代 步骤二 和 步骤三,直到两个中心点收敛到固定点。*( 或者可能根据我们所给的条件停止,如最大迭代次数,或达到特定的准去率等。) 这些点使得测试数据与其对应的中心点之间的距离之和最小。 或者简单地说,C1↔红色点 和 C2↔蓝色点 之间的距离之和最小。
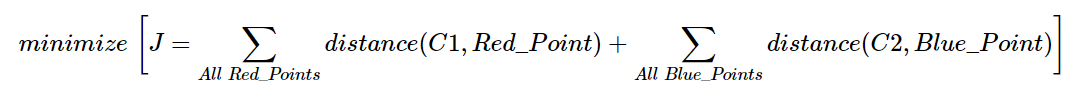
最终结果大概如下所示:
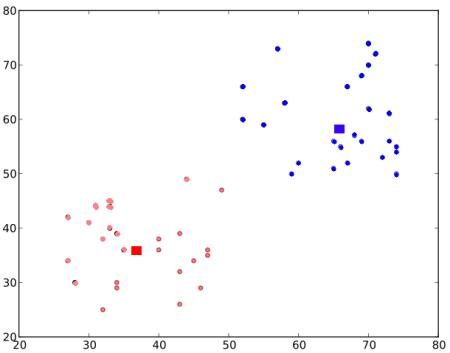
这只是对 K-Means 聚类的直观理解。有关更多详细信息和数学解释,请阅读任何规范的机器学习教科书或阅读额外资源中的链接。这只是 K-Means 聚类的顶层。这个算法有很多修改,如如何选择初始中心点,如何加速迭代过程等。
 极客笔记
极客笔记