在本教程中:
- 你会学到简单阈值法,自适应阈值法,以及 Otsu 阈值法(俗称大津法)等。
- 你会学到如下函数:cv.threshold,cv.adaptiveThreshold 等。
OpenCV简单阈值法
此方法是直截了当的。如果像素值大于阈值,则会被赋为一个值(可能为白色),否则会赋为另一个值(可能为黑色)。使用的函数是 cv.threshold。第一个参数是源图像,它应该是灰度图像。第二个参数是阈值,用于对像素值进行分类。第三个参数是 maxval,它表示像素值大于(有时小于)阈值时要给定的值。opencv 提供了不同类型的阈值,由函数的第四个参数决定。不同的类型有:
文档清楚地解释了每种类型的含义。请查看文档。
获得两个输出。第一个是 retval,稍后将解释。第二个输出是我们的阈值图像。
代码如下:
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
img = cv.imread('gradient.png',0)
ret,thresh1 = cv.threshold(img,127,255,cv.THRESH_BINARY)
ret,thresh2 = cv.threshold(img,127,255,cv.THRESH_BINARY_INV)
ret,thresh3 = cv.threshold(img,127,255,cv.THRESH_TRUNC)
ret,thresh4 = cv.threshold(img,127,255,cv.THRESH_TOZERO)
ret,thresh5 = cv.threshold(img,127,255,cv.THRESH_TOZERO_INV)
titles = ['Original Image','BINARY','BINARY_INV','TRUNC','TOZERO','TOZERO_INV']
images = [img, thresh1, thresh2, thresh3, thresh4, thresh5]
for i in xrange(6):
plt.subplot(2,3,i+1),plt.imshow(images[i],'gray')
plt.title(titles[i])
plt.xticks([]),plt.yticks([])
plt.show()
注意
绘制多个图像,我们使用 plt.subplot()函数。有关详细信息,请查看 Matplotlib 文档。
结果如下所示:

OpenCV自适应阈值
在前一节中,我们使用一个全局变量作为阈值。但在图像在不同区域具有不同照明条件的条件下,这可能不是很好。在这种情况下,我们采用自适应阈值。在此,算法计算图像的一个小区域的阈值。因此,我们得到了同一图像不同区域的不同阈值,对于不同光照下的图像,得到了更好的结果。
它有三个“特殊”输入参数,只有一个输出参数。
Adaptive Method-它决定如何计算阈值。
- cv.ADAPTIVE_THRESH_MEAN_C 阈值是指邻近地区的平均值。
- cv.ADAPTIVE_THRESH_GAUSSIAN_C 阈值是权重为高斯窗的邻域值的加权和。
Block Size-它决定了计算阈值的窗口区域的大小。
C-它只是一个常数,会从平均值或加权平均值中减去该值。
下面的代码比较了具有不同照明的图像的全局阈值和自适应阈值:
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
img = cv.imread('sudoku.png',0)
img = cv.medianBlur(img,5)
ret,th1 = cv.threshold(img,127,255,cv.THRESH_BINARY)
th2 = cv.adaptiveThreshold(img,255,cv.ADAPTIVE_THRESH_MEAN_C,\
cv.THRESH_BINARY,11,2)
th3 = cv.adaptiveThreshold(img,255,cv.ADAPTIVE_THRESH_GAUSSIAN_C,\
cv.THRESH_BINARY,11,2)
titles = ['Original Image', 'Global Thresholding (v = 127)',
'Adaptive Mean Thresholding', 'Adaptive Gaussian Thresholding']
images = [img, th1, th2, th3]
for i in xrange(4):
plt.subplot(2,2,i+1),plt.imshow(images[i],'gray')
plt.title(titles[i])
plt.xticks([]),plt.yticks([])
plt.show()
结果如下所示:

OpenCV Otsu 二值化
在第一部分中,我告诉过您有一个参数 retval。当我们进行 Otsu 二值化时,它的用途就来了。那是什么?
在全局阈值化中,我们使用一个任意的阈值,对吗?那么,我们如何知道我们选择的值是好的还是不好的呢?答案是,试错法。但是考虑一个双峰图像(简单来说,双峰图像是一个直方图有两个峰值的图像)。对于那个图像,我们可以近似地取这些峰值中间的一个值作为阈值,对吗?这就是 Otsu 二值化所做的。所以简单来说,它会自动从双峰图像的图像直方图中计算出阈值。(对于非双峰图像,二值化将不准确。)
为此,我们使用了 cv.threshold 函数,但传递了一个额外的符号 cv.THRESH_OTSU 。对于阈值,只需传入零。然后,该算法找到最佳阈值,并作为第二个输出返回 retval。如果不使用 otsu 阈值,则 retval 与你使用的阈值相同。
查看下面的示例。输入图像是噪声图像。在第一种情况下,我应用了值为 127 的全局阈值。在第二种情况下,我直接应用 otsu 阈值。在第三种情况下,我使用 5×5 高斯核过滤图像以去除噪声,然后应用 otsu 阈值。查看噪声过滤如何改进结果。
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
img = cv.imread('noisy2.png',0)
# 全局阈值
ret1,th1 = cv.threshold(img,127,255,cv.THRESH_BINARY)
# Otsu 阈值
ret2,th2 = cv.threshold(img,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
# 经过高斯滤波的 Otsu 阈值
blur = cv.GaussianBlur(img,(5,5),0)
ret3,th3 = cv.threshold(blur,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
# 画出所有的图像和他们的直方图
images = [img, 0, th1,
img, 0, th2,
blur, 0, th3]
titles = ['Original Noisy Image','Histogram','Global Thresholding (v=127)',
'Original Noisy Image','Histogram',"Otsu's Thresholding",
'Gaussian filtered Image','Histogram',"Otsu's Thresholding"]
for i in xrange(3):
plt.subplot(3,3,i*3+1),plt.imshow(images[i*3],'gray')
plt.title(titles[i*3]), plt.xticks([]), plt.yticks([])
plt.subplot(3,3,i*3+2),plt.hist(images[i*3].ravel(),256)
plt.title(titles[i*3+1]), plt.xticks([]), plt.yticks([])
plt.subplot(3,3,i*3+3),plt.imshow(images[i*3+2],'gray')
plt.title(titles[i*3+2]), plt.xticks([]), plt.yticks([])
plt.show()
结果如下:

OpenCV Otsu 二值化原理
本节演示了 otsu 二值化的 python 实现,以展示它的实际工作原理。如果你不感兴趣,可以跳过这个。
由于我们使用的是双峰图像,因此 Otsu 的算法试图找到一个阈值(t),该阈值将由下式计算得到的类内加权方差最小化:
\sigma_w^2(t) = q_1(t)\sigma_1^2(t)+q_2(t)\sigma_2^2(t)
其中:
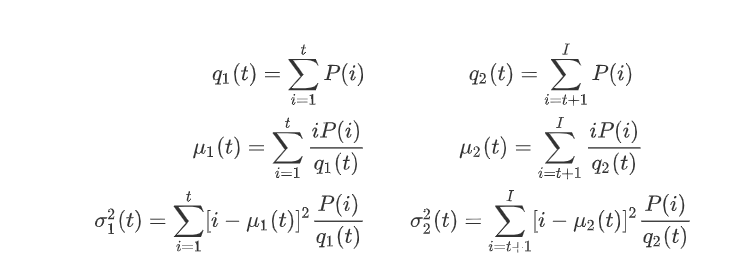
它实际上找到一个 T 值,它位于两个峰值之间,使得两个类的方差最小。它可以简单地在 python 中实现,如下所示:
img = cv.imread('noisy2.png',0)
blur = cv.GaussianBlur(img,(5,5),0)
# 找到归一化直方图还有累计分布函数
hist = cv.calcHist([blur],[0],None,[256],[0,256])
hist_norm = hist.ravel()/hist.max()
Q = hist_norm.cumsum()
bins = np.arange(256)
fn_min = np.inf
thresh = -1
for i in xrange(1,256):
p1,p2 = np.hsplit(hist_norm,[i]) # 概率
q1,q2 = Q[i],Q[255]-Q[i] # 类别总和
b1,b2 = np.hsplit(bins,[i]) # 权重
# f 找到均值与方差
m1,m2 = np.sum(p1*b1)/q1, np.sum(p2*b2)/q2
v1,v2 = np.sum(((b1-m1)**2)*p1)/q1,np.sum(((b2-m2)**2)*p2)/q2
# 计算最小函数
fn = v1*q1 + v2*q2
if fn < fn_min:
fn_min = fn
thresh = i
# 用 OpenCV 函数的 otsu'阈值
ret, otsu = cv.threshold(blur,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
print( "{} {}".format(thresh,ret) )
注意
这其中有很多新的函数,我们会在之后章节讲述。
 极客笔记
极客笔记