Matplotlib.pyplot.semilogy()函数:绘制半对数图的强大工具
参考:matplotlib.pyplot.semilogy() function in Python
Matplotlib是Python中最流行的数据可视化库之一,它提供了丰富的绘图功能。在众多函数中,matplotlib.pyplot.semilogy()是一个非常有用的工具,专门用于绘制半对数图(semi-logarithmic plot)。本文将深入探讨这个函数的用法、特点和应用场景,帮助读者充分掌握这一强大的可视化工具。
1. 什么是半对数图?
在开始介绍semilogy()函数之前,我们需要先了解什么是半对数图。半对数图是一种特殊的二维图表,其中一个轴(通常是y轴)使用对数刻度,而另一个轴(通常是x轴)使用线性刻度。这种图表在处理跨越多个数量级的数据时特别有用,因为它可以在一个图表中同时显示大小差异很大的数值。
半对数图在科学、工程和金融等领域广泛应用,特别适合展示指数增长或衰减的数据,如人口增长、放射性衰变、声音强度等。
2. semilogy()函数的基本用法
semilogy()函数是matplotlib.pyplot模块中的一个函数,用于创建y轴为对数刻度的半对数图。它的基本语法如下:
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 10, 100)
y = np.exp(x)
plt.semilogy(x, y)
plt.title('How2matplotlib.com - Basic Semilogy Plot')
plt.xlabel('X-axis (Linear)')
plt.ylabel('Y-axis (Log)')
plt.show()
Output:
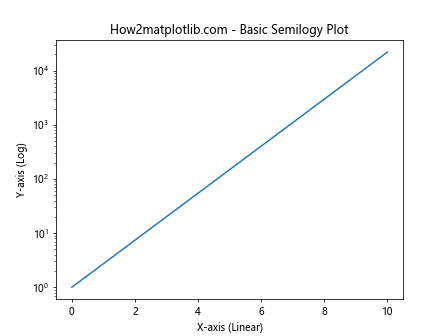
在这个例子中,我们创建了一个简单的半对数图。x轴是线性的,范围从0到10,而y轴是对数刻度的,显示了e^x的值。这个图清晰地展示了指数函数的快速增长特性。
3. 自定义semilogy()图表
semilogy()函数提供了多种自定义选项,让我们能够根据需求调整图表的外观。以下是一些常用的自定义方法:
3.1 设置线条样式和颜色
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y1 = np.exp(x)
y2 = np.exp(x/2)
plt.semilogy(x, y1, 'r--', label='how2matplotlib.com - exp(x)')
plt.semilogy(x, y2, 'b-.', label='how2matplotlib.com - exp(x/2)')
plt.legend()
plt.title('Custom Line Styles in Semilogy Plot')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (Log)')
plt.show()
Output:
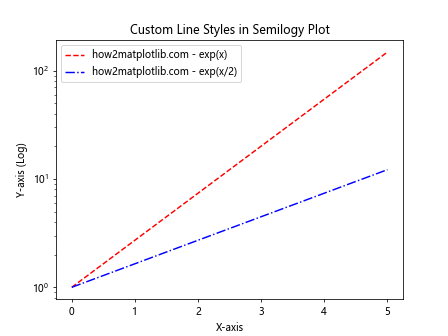
在这个例子中,我们绘制了两条曲线,分别使用红色虚线和蓝色点划线。通过设置不同的线条样式和颜色,我们可以轻松区分不同的数据系列。
3.2 添加网格线
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y = np.exp(x)
plt.semilogy(x, y)
plt.grid(True, which="both", ls="-", color='0.65')
plt.title('How2matplotlib.com - Semilogy Plot with Grid')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (Log)')
plt.show()
Output:
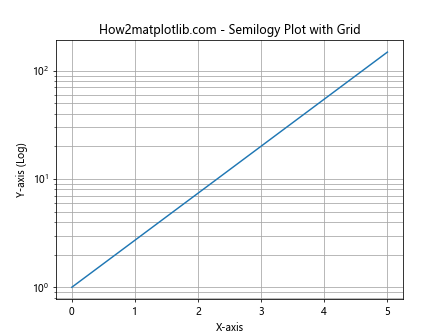
这个例子展示了如何在半对数图中添加网格线。网格线可以帮助读者更准确地读取数据点的值。
3.3 设置y轴的范围
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y = np.exp(x)
plt.semilogy(x, y)
plt.ylim(1, 1000)
plt.title('How2matplotlib.com - Semilogy Plot with Y-axis Limits')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (Log)')
plt.show()
Output:
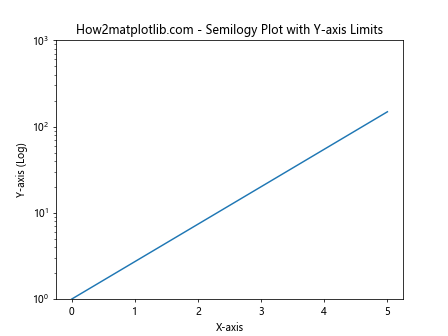
通过使用ylim()函数,我们可以设置y轴的显示范围。这在需要聚焦于特定数值范围时非常有用。
4. 多数据系列的半对数图
semilogy()函数不仅可以绘制单一数据系列,还可以在同一图表中展示多个数据系列,这对于比较不同数据集非常有用。
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y1 = np.exp(x)
y2 = np.exp(x/2)
y3 = np.exp(x/3)
plt.semilogy(x, y1, 'r-', label='how2matplotlib.com - exp(x)')
plt.semilogy(x, y2, 'g--', label='how2matplotlib.com - exp(x/2)')
plt.semilogy(x, y3, 'b:', label='how2matplotlib.com - exp(x/3)')
plt.legend()
plt.title('Multiple Series in Semilogy Plot')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (Log)')
plt.show()
Output:
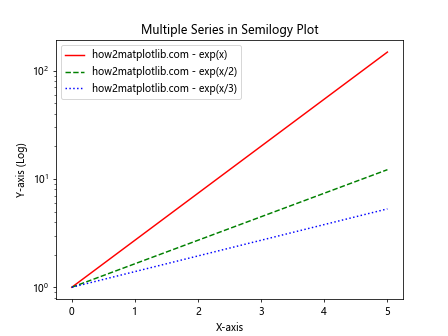
这个例子展示了如何在一个半对数图中绘制三个不同的指数函数。通过使用不同的颜色和线型,我们可以清晰地区分每个数据系列。
5. 结合其他pyplot函数
semilogy()函数可以与其他pyplot函数结合使用,以创建更复杂和信息丰富的图表。
5.1 添加文本注释
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y = np.exp(x)
plt.semilogy(x, y)
plt.annotate('how2matplotlib.com\nExponential growth', xy=(3, np.exp(3)), xytext=(4, 10),
arrowprops=dict(facecolor='black', shrink=0.05))
plt.title('Semilogy Plot with Annotation')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (Log)')
plt.show()
Output:
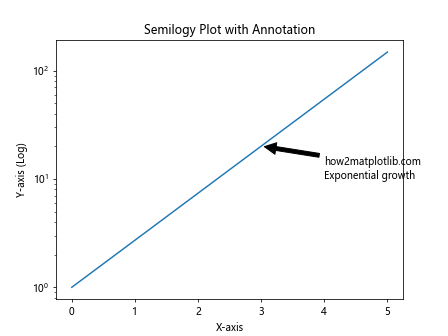
这个例子展示了如何在半对数图中添加文本注释。注释可以帮助解释图表中的特定特征或趋势。
5.2 添加次要刻度
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y = np.exp(x)
fig, ax = plt.subplots()
ax.semilogy(x, y)
ax.set_title('How2matplotlib.com - Semilogy Plot with Minor Ticks')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (Log)')
ax.minorticks_on()
ax.grid(True, which='both', linestyle=':', color='gray')
plt.show()
Output:
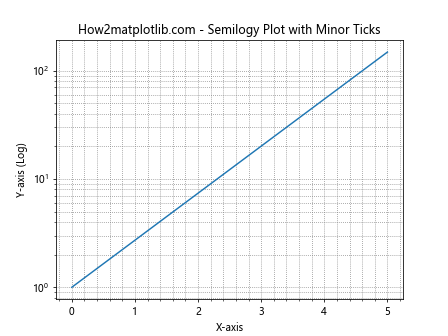
这个例子展示了如何在半对数图中添加次要刻度。次要刻度可以提高图表的精确度,使读者更容易估计数值。
6. 处理实际数据
虽然前面的例子都使用了理论函数,但semilogy()函数在处理实际数据时也非常有用。以下是一个使用真实数据的例子:
import matplotlib.pyplot as plt
import numpy as np
# 模拟某城市10年的人口数据
years = np.arange(2010, 2021)
population = np.array([100000, 120000, 150000, 200000, 280000, 400000, 600000, 900000, 1400000, 2200000, 3500000])
plt.semilogy(years, population, 'bo-')
plt.title('How2matplotlib.com - City Population Growth (2010-2020)')
plt.xlabel('Year')
plt.ylabel('Population (Log Scale)')
plt.grid(True, which="both", ls="-", color='0.65')
plt.show()
Output:
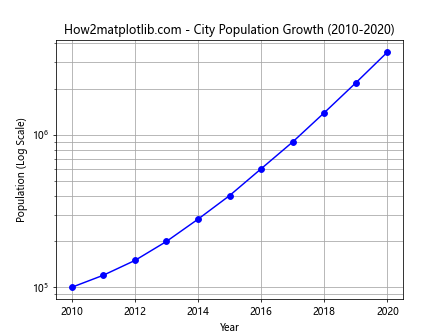
这个例子模拟了一个城市10年的人口增长数据。使用半对数图可以清晰地展示人口的指数增长趋势。
7. 比较线性图和半对数图
为了更好地理解半对数图的优势,我们可以将其与普通的线性图进行比较:
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y = np.exp(x)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# 线性图
ax1.plot(x, y)
ax1.set_title('How2matplotlib.com - Linear Plot')
ax1.set_xlabel('X-axis')
ax1.set_ylabel('Y-axis')
# 半对数图
ax2.semilogy(x, y)
ax2.set_title('How2matplotlib.com - Semilogy Plot')
ax2.set_xlabel('X-axis')
ax2.set_ylabel('Y-axis (Log)')
plt.tight_layout()
plt.show()
Output:
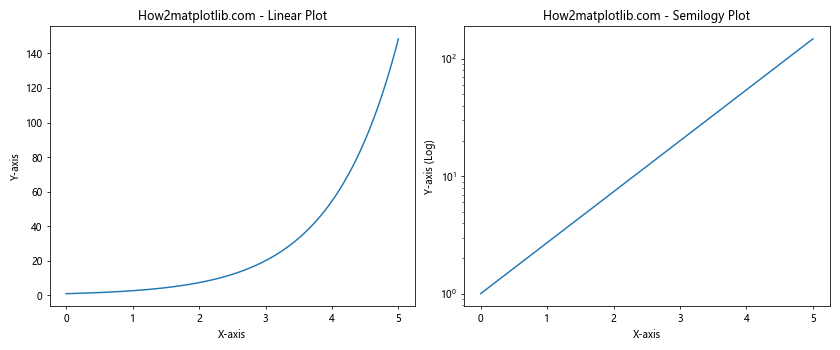
这个例子并排展示了同一数据的线性图和半对数图。通过比较,我们可以看到半对数图如何更好地展示了指数增长的特性。
8. 自定义y轴刻度
有时,我们可能需要自定义y轴的刻度标签。以下是一个例子:
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y = np.exp(x)
fig, ax = plt.subplots()
ax.semilogy(x, y)
ax.set_title('How2matplotlib.com - Custom Y-axis Ticks')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (Log)')
# 自定义y轴刻度
y_ticks = [1, 10, 100, 1000]
ax.set_yticks(y_ticks)
ax.set_yticklabels([f'{tick:,}' for tick in y_ticks])
plt.show()
Output:
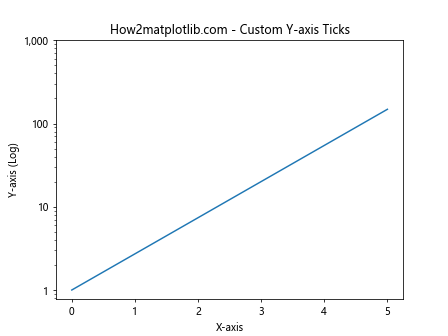
在这个例子中,我们自定义了y轴的刻度,并使用逗号分隔符格式化了刻度标签。
9. 处理负值和零值
半对数图在处理负值和零值时需要特别注意,因为对数函数在这些值上是未定义的。以下是一个处理这种情况的例子:
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-5, 5, 100)
y = x**3 - x
plt.semilogy(x, np.abs(y), label='how2matplotlib.com - |x^3 - x|')
plt.semilogy(x, np.maximum(y, 1e-10), label='how2matplotlib.com - max(x^3 - x, 1e-10)')
plt.legend()
plt.title('Handling Negative and Zero Values in Semilogy Plot')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (Log)')
plt.grid(True)
plt.show()
Output:
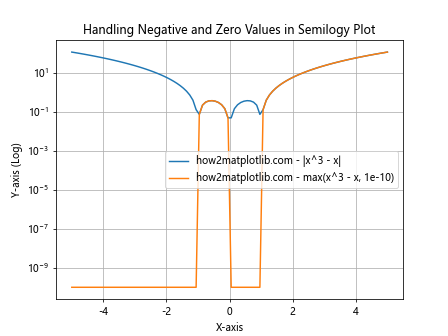
这个例子展示了两种处理负值和零值的方法:取绝对值和使用最小阈值。
10. 结合其他类型的图表
semilogy()函数可以与其他类型的图表结合使用,创建更复杂的可视化效果。以下是一个结合柱状图的例子:
import matplotlib.pyplot as plt
import numpy as np
categories = ['A', 'B', 'C', 'D', 'E']
values = [10, 100, 1000, 10000, 100000]
fig, ax = plt.subplots()
ax.bar(categories, values)
ax.set_yscale('log')
ax.set_title('How2matplotlib.com - Bar Chart with Log Scale Y-axis')
ax.set_xlabel('Categories')
ax.set_ylabel('Values (Log Scale)')
for i, v in enumerate(values):
ax.text(i, v, str(v), ha='center', va='bottom')
plt.show()
Output:
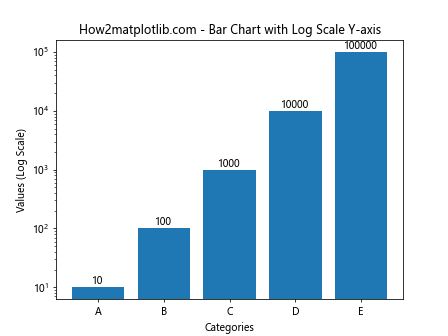
这个例子创建了一个y轴为对数刻度的柱状图,展示了如何将semilogy()的概念应用到其他类型的图表中。
11. 使用subplots创建多个半对数图
当需要比较多个相关但独立的数据集时,创建多个子图可能会很有用。以下是一个使用subplots创建多个半对数图的例子:
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y1 = np.exp(x)
y2 = np.exp(x/2)
y3 = np.exp(x/3)
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(8, 12))
ax1.semilogy(x, y1)
ax1.set_title('How2matplotlib.com - exp(x)')
ax1.set_xlabel('X-axis')
ax1.set_ylabel('Y-axis (Log)')
ax2.semilogy(x, y2)
ax2.set_title('How2matplotlib.com - exp(x/2)')
ax2.set_xlabel('X-axis')
ax2.set_ylabel('Y-axis (Log)')
ax3.semilogy(x, y3)
ax3.set_title('How2matplotlib.com - exp(x/3)')
ax3.set_xlabel('X-axis')
ax3.set_ylabel('Y-axis (Log)')
plt.tight_layout()
plt.show()
Output:
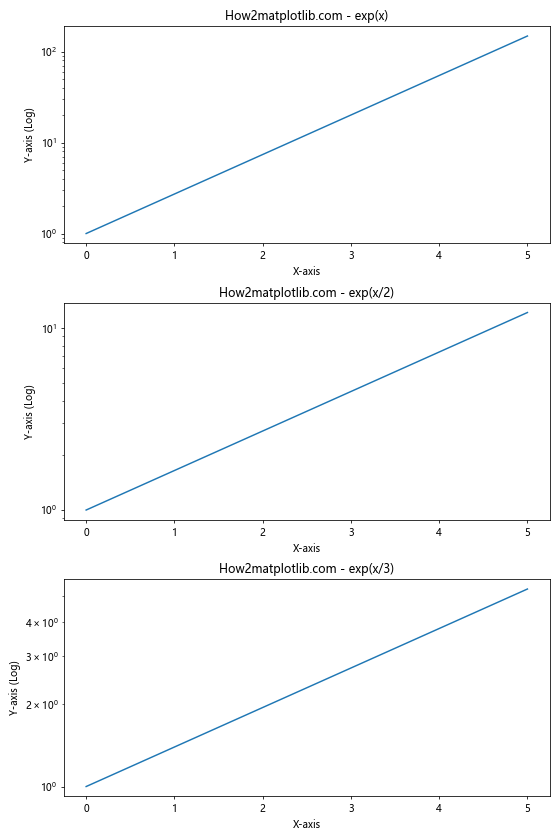
这个例子创建了三个垂直排列的半对数图,每个图表示不同的指数函数。这种布局允许我们直观地比较不同函数的增长率。
12. 使用颜色映射
颜色映射可以为半对数图添加额外的维度,特别是当我们需要表示第三个变量时。以下是一个使用颜色映射的例子:
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y = np.exp(x)
z = x**2
plt.figure(figsize=(10, 6))
scatter = plt.scatter(x, y, c=z, cmap='viridis', s=50)
plt.yscale('log')
plt.colorbar(scatter, label='z = x^2')
plt.title('How2matplotlib.com - Semilogy Plot with Color Mapping')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (Log)')
plt.show()
Output:
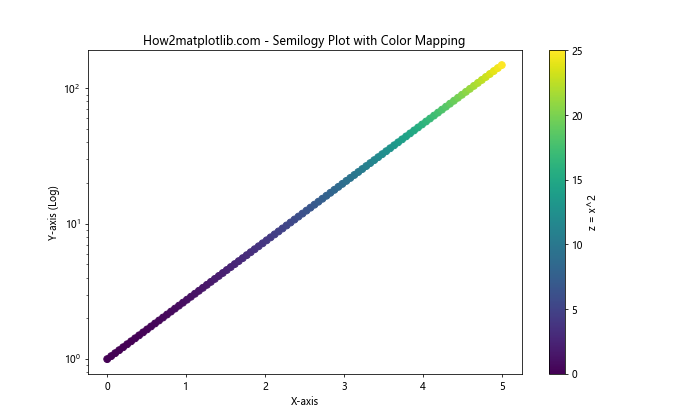
在这个例子中,我们使用散点图和颜色映射来表示三个变量:x、y(在对数刻度上)和z(通过颜色表示)。这种方法可以在二维图表中有效地展示三维数据。
13. 动态更新的半对数图
在某些应用中,我们可能需要实时更新数据并重绘图表。以下是一个简单的动态更新半对数图的例子:
import matplotlib.pyplot as plt
import numpy as np
import time
plt.ion() # 打开交互模式
fig, ax = plt.subplots()
x = np.linspace(0, 2, 100)
line, = ax.semilogy(x, np.exp(x))
ax.set_ylim(1, 1000)
ax.set_title('How2matplotlib.com - Dynamic Semilogy Plot')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (Log)')
for i in range(100):
new_y = np.exp(x * (1 + i/100))
line.set_ydata(new_y)
fig.canvas.draw()
fig.canvas.flush_events()
time.sleep(0.1)
plt.ioff() # 关闭交互模式
plt.show()
Output:
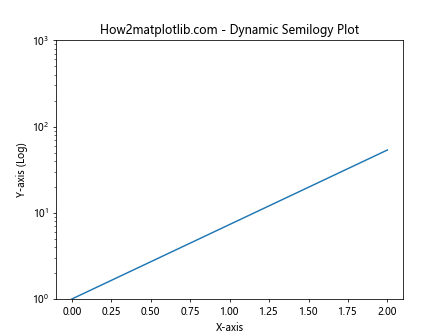
这个例子创建了一个动态更新的半对数图,展示了指数函数随时间变化的情况。
14. 使用填充区域
在某些情况下,我们可能想要强调某个区域或显示数据的不确定性范围。以下是一个使用填充区域的半对数图例子:
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y = np.exp(x)
y_lower = np.exp(x) * 0.9
y_upper = np.exp(x) * 1.1
plt.figure(figsize=(10, 6))
plt.semilogy(x, y, 'r-', label='how2matplotlib.com - exp(x)')
plt.fill_between(x, y_lower, y_upper, alpha=0.2, color='r')
plt.legend()
plt.title('Semilogy Plot with Filled Area')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (Log)')
plt.show()
Output:
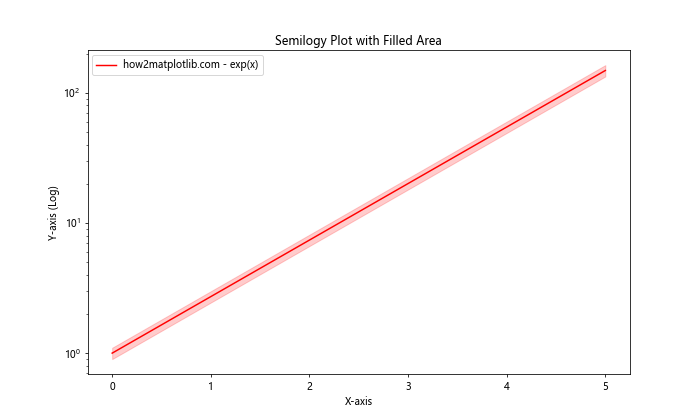
这个例子展示了如何在半对数图中添加填充区域,可以用来表示数据的置信区间或误差范围。
15. 处理日期数据
半对数图也可以用于处理时间序列数据。以下是一个使用日期数据的例子:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# 创建一个日期范围
dates = pd.date_range(start='2020-01-01', end='2020-12-31', freq='D')
values = np.cumsum(np.random.randn(len(dates))) + 100
plt.figure(figsize=(12, 6))
plt.semilogy(dates, values)
plt.title('How2matplotlib.com - Semilogy Plot with Date Data')
plt.xlabel('Date')
plt.ylabel('Value (Log Scale)')
plt.grid(True)
plt.gcf().autofmt_xdate() # 自动格式化x轴日期标签
plt.show()
Output:
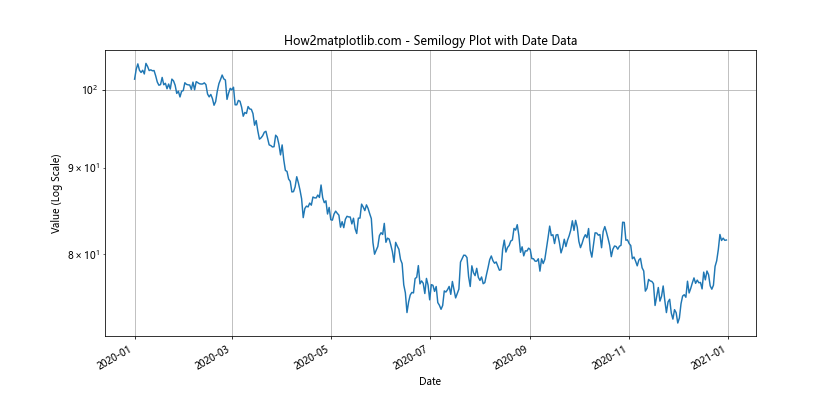
这个例子展示了如何创建一个基于日期的半对数图,适用于展示股票价格、累积收益等随时间变化的数据。
16. 结合极坐标系
虽然semilogy()通常用于笛卡尔坐标系,但我们也可以将其概念应用到极坐标系中:
import matplotlib.pyplot as plt
import numpy as np
theta = np.linspace(0, 2*np.pi, 100)
r = np.exp(theta)
fig, ax = plt.subplots(subplot_kw=dict(projection='polar'))
ax.plot(theta, r)
ax.set_title('How2matplotlib.com - Polar Plot with Log Scale Radius')
ax.set_rscale('log')
ax.set_rticks([1, 10, 100])
plt.show()
Output:
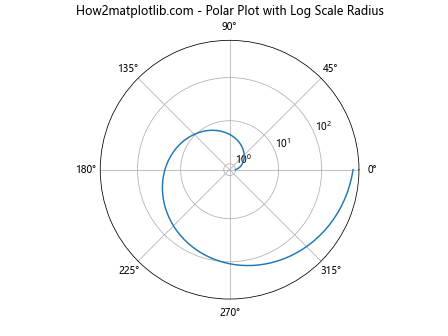
这个例子创建了一个极坐标图,其中径向轴使用对数刻度。这种图表可以用于展示具有周期性和指数增长特性的数据。
17. 使用双对数刻度
虽然semilogy()函数专门用于创建y轴为对数刻度的图表,但有时我们可能需要x轴和y轴都使用对数刻度。这可以通过loglog()函数实现:
import matplotlib.pyplot as plt
import numpy as np
x = np.logspace(0, 5, 100)
y = x**2
plt.figure(figsize=(10, 6))
plt.loglog(x, y, label='how2matplotlib.com - y = x^2')
plt.title('Log-Log Plot')
plt.xlabel('X-axis (Log Scale)')
plt.ylabel('Y-axis (Log Scale)')
plt.legend()
plt.grid(True)
plt.show()
Output:
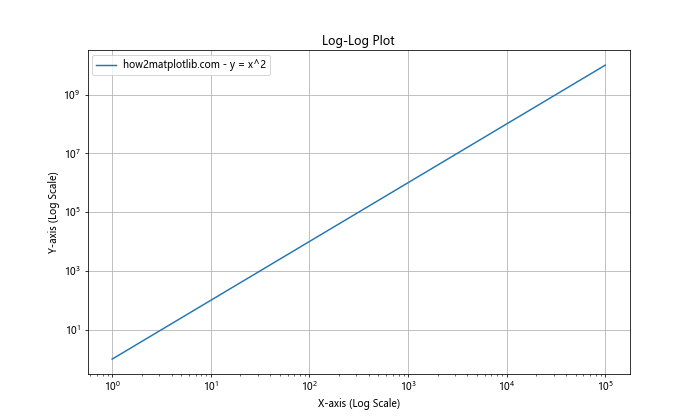
这个例子展示了如何创建双对数图,这种图表在处理幂律关系或跨越多个数量级的数据时特别有用。
18. 自定义刻度格式化器
有时,我们可能需要自定义刻度标签的格式。以下是一个使用自定义格式化器的例子:
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import FuncFormatter
def format_func(value, tick_number):
return f'{value:.0e}'
x = np.linspace(0, 5, 100)
y = np.exp(x)
fig, ax = plt.subplots()
ax.semilogy(x, y)
ax.yaxis.set_major_formatter(FuncFormatter(format_func))
ax.set_title('How2matplotlib.com - Semilogy Plot with Custom Formatter')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (Log)')
plt.show()
Output:
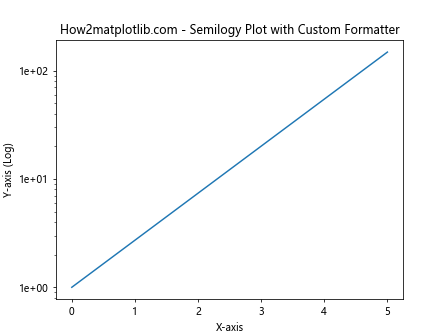
这个例子使用了自定义的格式化函数来将y轴的刻度标签显示为科学记数法。
19. 结合箱线图
半对数刻度也可以应用于其他类型的统计图表,如箱线图:
import matplotlib.pyplot as plt
import numpy as np
data = [np.random.lognormal(0, s, 1000) for s in range(1, 5)]
fig, ax = plt.subplots()
ax.boxplot(data)
ax.set_yscale('log')
ax.set_title('How2matplotlib.com - Box Plot with Log Scale Y-axis')
ax.set_xlabel('Group')
ax.set_ylabel('Value (Log Scale)')
plt.show()
Output:
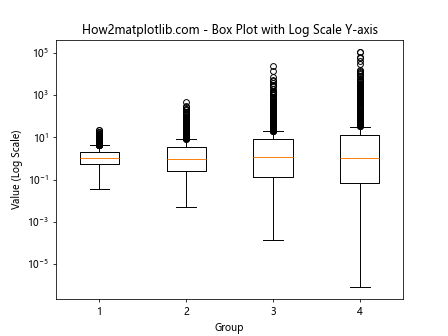
这个例子创建了一个y轴为对数刻度的箱线图,适用于比较不同组之间的对数正态分布数据。
20. 使用样式表
Matplotlib提供了多种预定义的样式表,可以快速改变图表的整体外观:
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
y = np.exp(x)
plt.style.use('seaborn')
plt.figure(figsize=(10, 6))
plt.semilogy(x, y)
plt.title('How2matplotlib.com - Semilogy Plot with Seaborn Style')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (Log)')
plt.grid(True)
plt.show()
这个例子使用了’seaborn’样式,给半对数图带来了更现代化的外观。
总结
matplotlib.pyplot.semilogy()函数是一个强大的工具,用于创建半对数图。它在处理跨越多个数量级的数据、展示指数增长或衰减趋势时特别有用。通过本文的详细介绍和多样化的示例,我们探索了semilogy()函数的各种用法和技巧,从基本绘图到高级定制,再到与其他可视化技术的结合。
半对数图在科学研究、工程分析、金融建模等多个领域都有广泛应用。掌握semilogy()函数不仅能帮助我们更好地理解和展示数据,还能为数据分析和决策提供有力支持。
随着数据可视化在各个领域的重要性日益增加,熟练使用像semilogy()这样的专业工具变得越来越重要。希望本文能够帮助读者深入理解半对数图的概念和应用,并在实际工作中灵活运用这一强大的可视化技术。
 极客笔记
极客笔记