Matplotlib绘制基于离散点的等高线图:从基础到高级技巧
参考:matplotlib contour from points
Matplotlib是Python中最流行的数据可视化库之一,它提供了强大的工具来创建各种类型的图表和可视化效果。在本文中,我们将深入探讨如何使用Matplotlib绘制基于离散点的等高线图。等高线图是一种用于表示三维数据在二维平面上的投影的图形,它在地形图、气象学、物理学等多个领域都有广泛应用。我们将从基础概念开始,逐步深入到更高级的技巧,帮助你掌握这一强大的可视化工具。
1. 等高线图的基本概念
等高线图(Contour Plot)是一种用于表示三维数据在二维平面上的投影的图形。在等高线图中,相同高度(或值)的点被连接成线,这些线就是等高线。等高线图可以帮助我们直观地理解三维数据的分布和变化趋势。
在Matplotlib中,我们可以使用contour()和contourf()函数来绘制等高线图。contour()函数绘制线条等高线,而contourf()函数绘制填充等高线。
让我们从一个简单的例子开始:
import numpy as np
import matplotlib.pyplot as plt
# 创建数据点
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2))
# 绘制等高线图
plt.figure(figsize=(10, 8))
plt.contour(X, Y, Z, levels=20)
plt.title('How2matplotlib.com - Basic Contour Plot')
plt.xlabel('X')
plt.ylabel('Y')
plt.colorbar(label='Z')
plt.show()
Output:
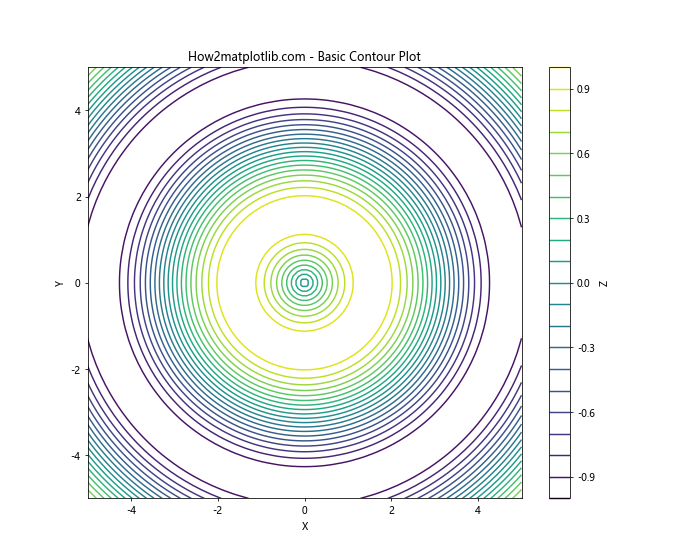
在这个例子中,我们首先创建了一个网格数据,然后使用contour()函数绘制等高线。levels参数指定了等高线的数量。
2. 从离散点生成等高线图
在实际应用中,我们经常需要从离散的数据点生成等高线图。这时,我们需要先将离散点插值到规则网格上,然后再绘制等高线图。
以下是一个从离散点生成等高线图的例子:
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import griddata
# 生成随机离散点
np.random.seed(0)
points = np.random.rand(1000, 2)
values = np.sin(points[:, 0] * 10) + np.cos(points[:, 1] * 10)
# 创建网格
grid_x, grid_y = np.mgrid[0:1:100j, 0:1:100j]
# 插值
grid_z = griddata(points, values, (grid_x, grid_y), method='cubic')
# 绘制等高线图
plt.figure(figsize=(10, 8))
plt.contourf(grid_x, grid_y, grid_z, levels=20, cmap='viridis')
plt.scatter(points[:, 0], points[:, 1], c='red', s=1)
plt.title('How2matplotlib.com - Contour Plot from Scattered Points')
plt.xlabel('X')
plt.ylabel('Y')
plt.colorbar(label='Z')
plt.show()
Output:
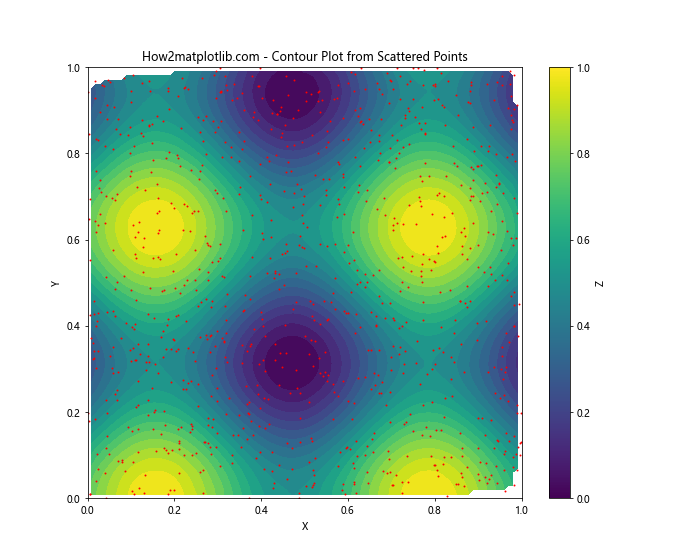
在这个例子中,我们首先生成了1000个随机点,然后使用scipy.interpolate.griddata函数将这些点插值到规则网格上。最后,我们使用contourf()函数绘制填充等高线图,并用红点标记原始数据点的位置。
3. 自定义等高线
Matplotlib提供了多种方法来自定义等高线的外观。我们可以控制等高线的颜色、线型、标签等属性。
以下是一个自定义等高线的例子:
import numpy as np
import matplotlib.pyplot as plt
# 创建数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2
# 绘制等高线图
plt.figure(figsize=(10, 8))
CS = plt.contour(X, Y, Z, levels=[0.5, 1, 2, 4, 8], colors=['r', 'g', 'b', 'c', 'm'])
plt.clabel(CS, inline=True, fontsize=10)
plt.title('How2matplotlib.com - Custom Contour Plot')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
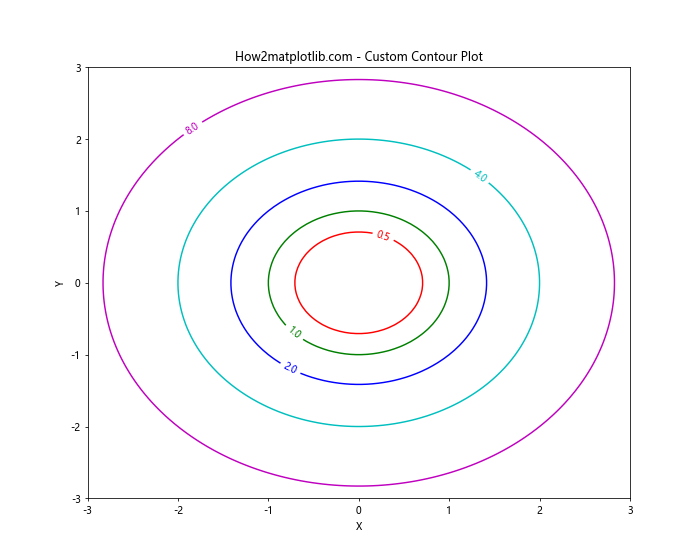
在这个例子中,我们使用levels参数指定了具体的等高线值,使用colors参数指定了每条等高线的颜色。clabel()函数用于在等高线上添加标签。
4. 等高线填充
除了线条等高线,我们还可以绘制填充等高线,这样可以更直观地展示数据的分布。
以下是一个绘制填充等高线的例子:
import numpy as np
import matplotlib.pyplot as plt
# 创建数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)
# 绘制填充等高线图
plt.figure(figsize=(10, 8))
plt.contourf(X, Y, Z, levels=20, cmap='RdYlBu')
plt.colorbar(label='Z')
plt.title('How2matplotlib.com - Filled Contour Plot')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
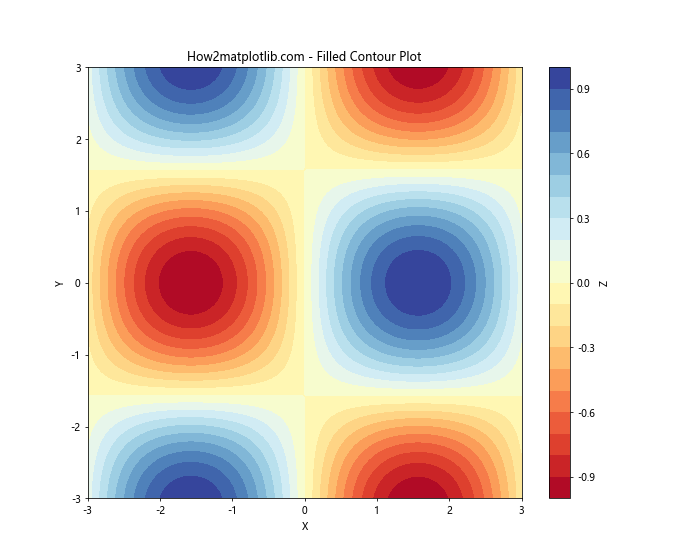
在这个例子中,我们使用contourf()函数绘制填充等高线图。cmap参数用于指定颜色映射。
5. 等高线图与其他图形的组合
等高线图可以与其他类型的图形组合,以提供更丰富的信息。例如,我们可以在等高线图上叠加散点图或向量场。
以下是一个将等高线图与散点图结合的例子:
import numpy as np
import matplotlib.pyplot as plt
# 创建数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)
# 生成随机点
np.random.seed(0)
points = np.random.rand(50, 2) * 6 - 3
values = np.sin(points[:, 0]) * np.cos(points[:, 1])
# 绘制等高线图和散点图
plt.figure(figsize=(10, 8))
plt.contourf(X, Y, Z, levels=20, cmap='viridis', alpha=0.8)
plt.scatter(points[:, 0], points[:, 1], c=values, cmap='viridis', edgecolors='w')
plt.colorbar(label='Z')
plt.title('How2matplotlib.com - Contour Plot with Scatter Points')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
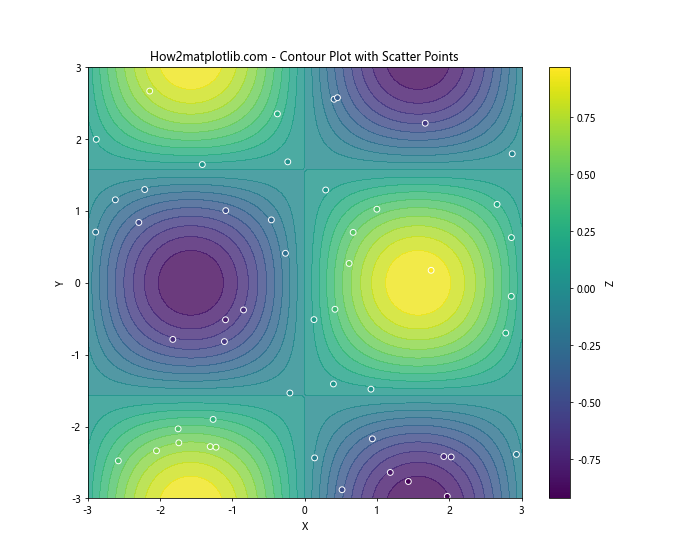
在这个例子中,我们首先绘制了填充等高线图,然后在其上叠加了一个散点图。散点的颜色与等高线图使用相同的颜色映射,以保持一致性。
6. 3D等高线图
虽然等高线图通常用于在2D平面上表示3D数据,但Matplotlib也支持在3D空间中绘制等高线图。这可以帮助我们更直观地理解数据的三维结构。
以下是一个3D等高线图的例子:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 创建数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2))
# 绘制3D等高线图
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.contour(X, Y, Z, levels=20, cmap='viridis')
ax.set_title('How2matplotlib.com - 3D Contour Plot')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
Output:
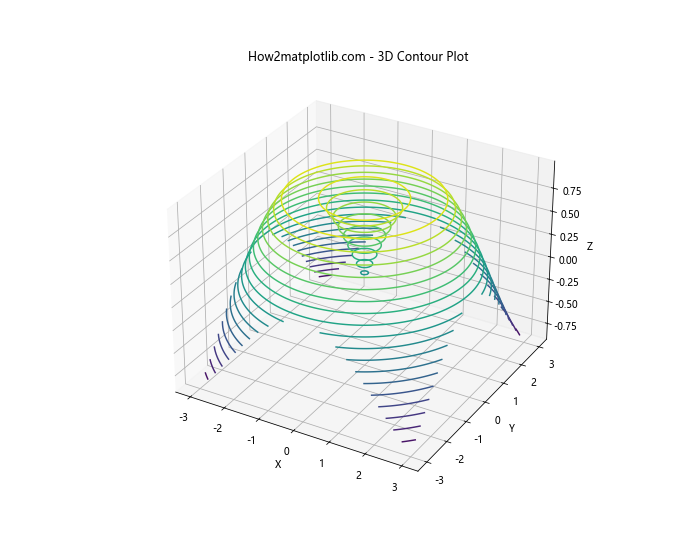
在这个例子中,我们使用mpl_toolkits.mplot3d模块创建了一个3D坐标系,然后在其中绘制了等高线图。
7. 等高线图的动画
动画可以帮助我们展示数据随时间的变化。Matplotlib提供了animation模块,使我们能够轻松创建动画等高线图。
以下是一个简单的等高线图动画例子:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# 创建数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
fig, ax = plt.subplots(figsize=(10, 8))
def update(frame):
ax.clear()
Z = np.sin(np.sqrt(X**2 + Y**2) - frame * 0.1)
cs = ax.contourf(X, Y, Z, levels=20, cmap='viridis')
ax.set_title(f'How2matplotlib.com - Animated Contour Plot (Frame {frame})')
ax.set_xlabel('X')
ax.set_ylabel('Y')
return cs
anim = FuncAnimation(fig, update, frames=100, interval=50)
plt.show()
Output:
在这个例子中,我们定义了一个update函数来更新每一帧的等高线图。FuncAnimation函数用于创建动画,它会重复调用update函数来生成每一帧。
8. 等高线图的标签和注释
为等高线图添加标签和注释可以帮助读者更好地理解数据。Matplotlib提供了多种方法来添加标签和注释。
以下是一个添加标签和注释的例子:
import numpy as np
import matplotlib.pyplot as plt
# 创建数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2
# 绘制等高线图
fig, ax = plt.subplots(figsize=(10, 8))
CS = ax.contour(X, Y, Z, levels=[0.5, 1, 2, 4, 8])
ax.clabel(CS, inline=True, fontsize=10)
# 添加文本注释
ax.text(0, 2, 'How2matplotlib.com\nPeak', ha='center', va='center', bbox=dict(facecolor='white', edgecolor='red', alpha=0.8))
# 添加箭头注释
ax.annotate('Slope', xy=(1, 1), xytext=(2, 2),
arrowprops=dict(facecolor='black', shrink=0.05))
ax.set_title('Contour Plot with Labels and Annotations')
ax.set_xlabel('X')
ax.set_ylabel('Y')
plt.show()
Output:
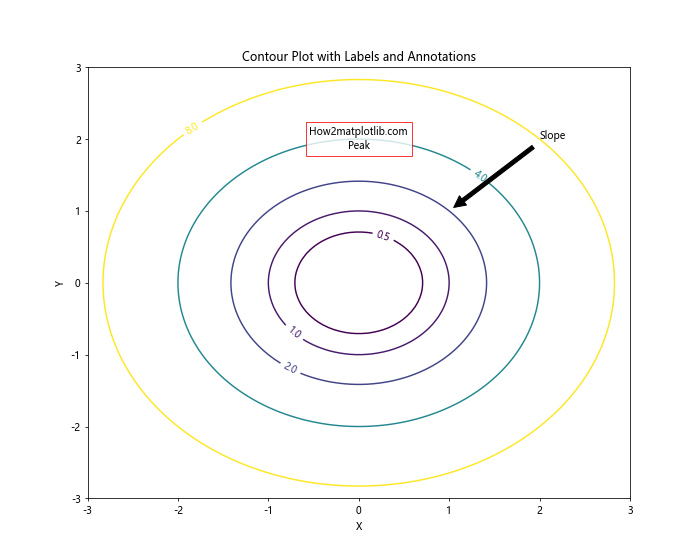
在这个例子中,我们使用clabel()函数为等高线添加标签,使用text()函数添加文本注释,使用annotate()函数添加带箭头的注释。
9. 等高线图的颜色映射
颜色映射(colormap)是等高线图中非常重要的一个元素,它决定了如何将数值映射到颜色。Matplotlib提供了多种内置的颜色映射,我们也可以创建自定义的颜色映射。
以下是一个使用不同颜色映射的例子:
import numpy as np
import matplotlib.pyplot as plt
# 创建数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)
# 创建子图
fig, axs = plt.subplots(2, 2, figsize=(12, 10))
cmaps = ['viridis', 'plasma', 'inferno', 'magma']
for ax, cmap in zip(axs.flat, cmaps):
cs = ax.contourf(X, Y, Z, levels=20, cmap=cmap)
fig.colorbar(cs, ax=ax, label='Z')
ax.set_title(f'How2matplotlib.com - {cmap.capitalize()} Colormap')
ax.set_xlabel('X')
ax.set_ylabel('Y')
plt.tight_layout()
plt.show()
Output:
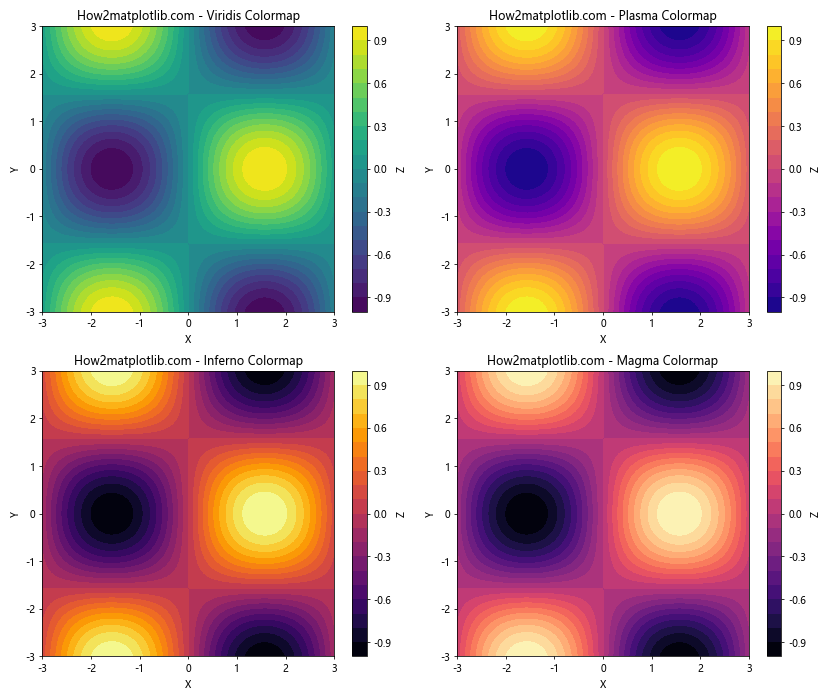
在这个例子中,我们使用了四种不同的颜色映射来绘制相同的等高线图,以展示颜色映射对可视化效果的影响。
10. 等高线图的插值方法
当我们从离散点生成等高线图时,插值方法的选择会影响最终的可视化效果。不同的插值方法适用于不同的数据分布和应用场景。
以下是一个比较不同插值方法的例子:
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import griddata
# 生成随机点
np.random.seed(0)
points = np.random.rand(1000, 2)
values = np.sin(points[:, 0] * 10) + np.cos(points[:, 1] * 10)
# 创建网格
grid_x, grid_y = np.mgrid[0:1:100j, 0:1:100j]
# 不同的插值方法
methods = ['nearest', 'linear', 'cubic']
fig, axs = plt.subplots(1, 3, figsize=(15, 5))
for ax, method in zip(axs, methods):
# 插值
grid_z = griddata(points, values, (grid_x, grid_y), method=method)
# 绘制等高线图
cs = ax.contourf(grid_x, grid_y, grid_z, levels=20, cmap='viridis')
ax.scatter(points[:, 0], points[:, 1], c='red', s=1)
ax.set_title(f'How2matplotlib.com - {method.capitalize()} Interpolation')
ax.set_xlabel('X')
ax.set_ylabel('Y')
fig.colorbar(cs, ax=ax, label='Z')
plt.tight_layout()
plt.show()
Output:
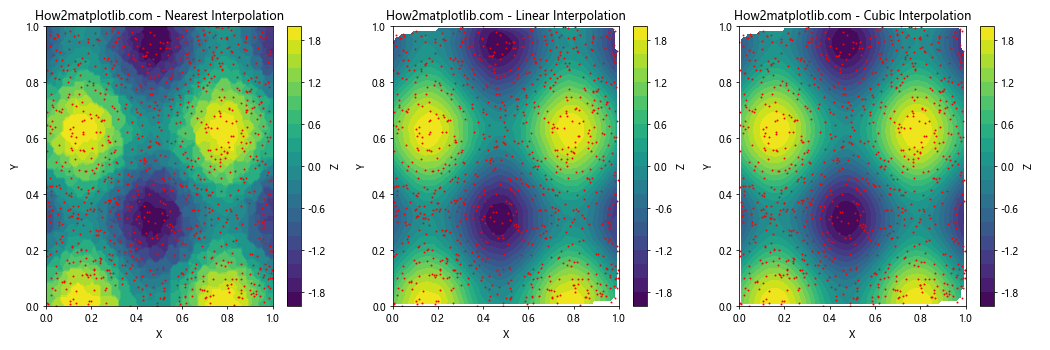
在这个例子中,我们比较了最近邻、线性和三次插值三种不同的插值方法。每种方法都会产生略有不同的等高线图,选择合适的插值方法可以帮助我们更准确地表示原始数据。
11. 等高线图的性能优化
当处理大量数据点时,绘制等高线图可能会变得很慢。以下是一些提高性能的技巧:
- 使用适当的数据采样:如果数据点过多,可以先进行降采样。
-
选择合适的插值方法:对于大型数据集,线性插值通常比三次插值快。
-
使用
tricontour和tricontourf:这些函数专门用于不规则网格,可能比常规的contour和contourf更快。
以下是一个使用tricontour的例子:
import numpy as np
import matplotlib.pyplot as plt
# 生成随机点
np.random.seed(0)
npts = 1000
x = np.random.uniform(-2, 2, npts)
y = np.random.uniform(-2, 2, npts)
z = x*np.exp(-x**2 - y**2)
# 绘制等高线图
plt.figure(figsize=(10, 8))
plt.tricontourf(x, y, z, levels=20, cmap='viridis')
plt.colorbar(label='Z')
plt.title('How2matplotlib.com - Tricontour Plot')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
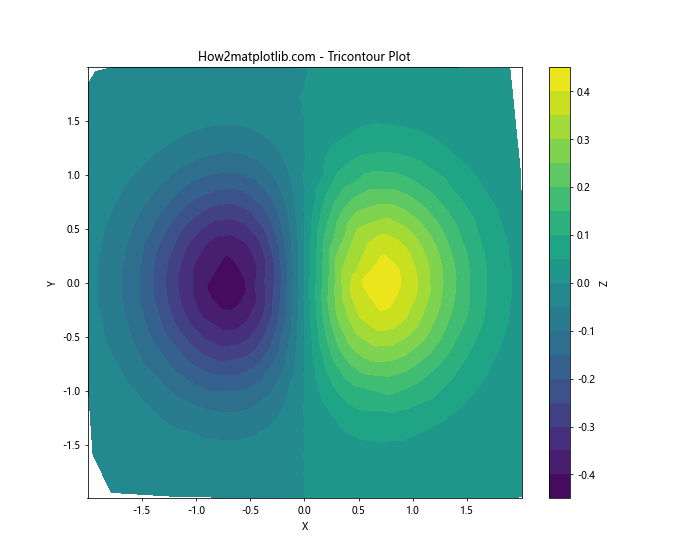
这个例子使用tricontourf直接从不规则点生成填充等高线图,无需先进行网格化。
12. 等高线图的统计分析
等高线图不仅可以用于可视化,还可以用于数据的统计分析。例如,我们可以计算特定等高线内的面积,或者找出数据的峰值和谷值。
以下是一个计算特定等高线内面积的例子:
import numpy as np
import matplotlib.pyplot as plt
from scipy import ndimage
# 创建数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = np.exp(-(X**2 + Y**2))
# 绘制等高线图
plt.figure(figsize=(10, 8))
CS = plt.contour(X, Y, Z, levels=[0.1, 0.5, 0.9])
plt.clabel(CS, inline=True, fontsize=10)
# 计算面积
areas = []
for level in CS.levels:
area = ndimage.measurements.sum(Z > level) * (x[1]-x[0])**2
areas.append(area)
plt.text(2, level, f'Area: {area:.2f}', verticalalignment='center')
plt.title('How2matplotlib.com - Contour Plot with Area Calculation')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
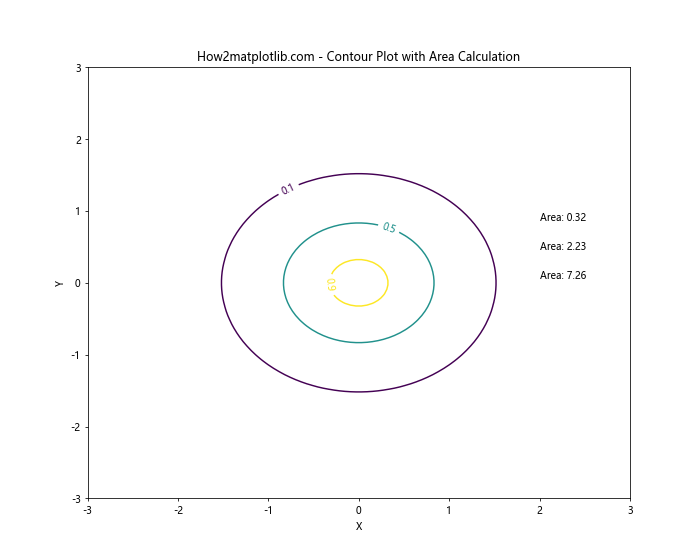
在这个例子中,我们计算了三个不同等高线内的面积,并将结果直接标注在图上。
13. 等高线图的误差分析
在科学和工程应用中,了解数据的不确定性和误差范围非常重要。我们可以使用等高线图来可视化数据的误差分布。
以下是一个展示数据及其误差范围的例子:
import numpy as np
import matplotlib.pyplot as plt
# 创建数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)
# 添加随机误差
np.random.seed(0)
error = np.random.normal(0, 0.1, Z.shape)
Z_with_error = Z + error
# 绘制等高线图
plt.figure(figsize=(10, 8))
CS = plt.contour(X, Y, Z, levels=10, colors='black', linewidths=2)
plt.clabel(CS, inline=True, fontsize=10)
# 绘制误差范围
plt.contourf(X, Y, np.abs(error), levels=10, cmap='Reds', alpha=0.5)
plt.colorbar(label='Error')
plt.title('How2matplotlib.com - Contour Plot with Error Analysis')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
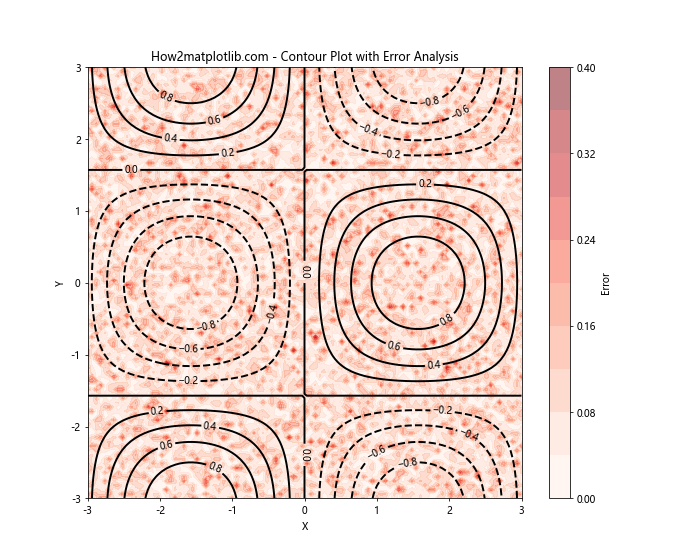
在这个例子中,我们使用黑色线条绘制了原始数据的等高线,然后使用红色填充表示了误差的分布。颜色越深的区域表示误差越大。
14. 等高线图的交互性
Matplotlib提供了一些交互式工具,可以让用户更好地探索等高线图。例如,我们可以添加一个滑块来动态调整等高线的数量。
以下是一个使用滑块调整等高线数量的例子:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider
# 创建数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)
# 创建图形和轴
fig, ax = plt.subplots(figsize=(10, 8))
plt.subplots_adjust(bottom=0.25)
# 初始绘制
contour = ax.contourf(X, Y, Z, levels=20, cmap='viridis')
plt.colorbar(contour, label='Z')
# 创建滑块
ax_slider = plt.axes([0.2, 0.1, 0.6, 0.03])
slider = Slider(ax_slider, 'Levels', 5, 50, valinit=20, valstep=1)
# 更新函数
def update(val):
ax.clear()
contour = ax.contourf(X, Y, Z, levels=int(slider.val), cmap='viridis')
ax.set_title(f'How2matplotlib.com - Contour Plot with {int(slider.val)} Levels')
ax.set_xlabel('X')
ax.set_ylabel('Y')
slider.on_changed(update)
plt.show()
Output:
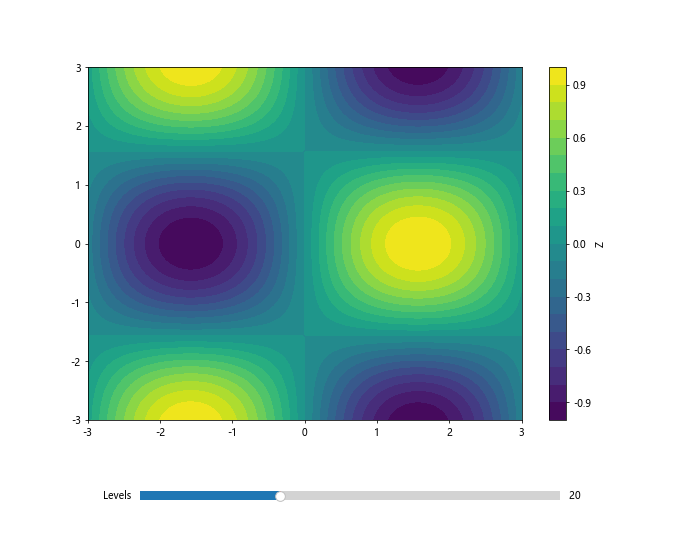
在这个例子中,我们创建了一个滑块,允许用户动态调整等高线的数量。当滑块值改变时,update函数会重新绘制等高线图。
15. 等高线图的导出和保存
在完成等高线图的绘制后,我们通常需要将其保存为图像文件或将数据导出以供进一步分析。Matplotlib提供了多种方式来保存图形。
以下是一个保存等高线图为不同格式的例子:
import numpy as np
import matplotlib.pyplot as plt
# 创建数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)
# 绘制等高线图
plt.figure(figsize=(10, 8))
plt.contourf(X, Y, Z, levels=20, cmap='viridis')
plt.colorbar(label='Z')
plt.title('How2matplotlib.com - Contour Plot for Export')
plt.xlabel('X')
plt.ylabel('Y')
# 保存为不同格式
plt.savefig('contour_plot.png', dpi=300) # PNG格式
plt.savefig('contour_plot.pdf') # PDF格式
plt.savefig('contour_plot.svg') # SVG格式
plt.show()
Output:
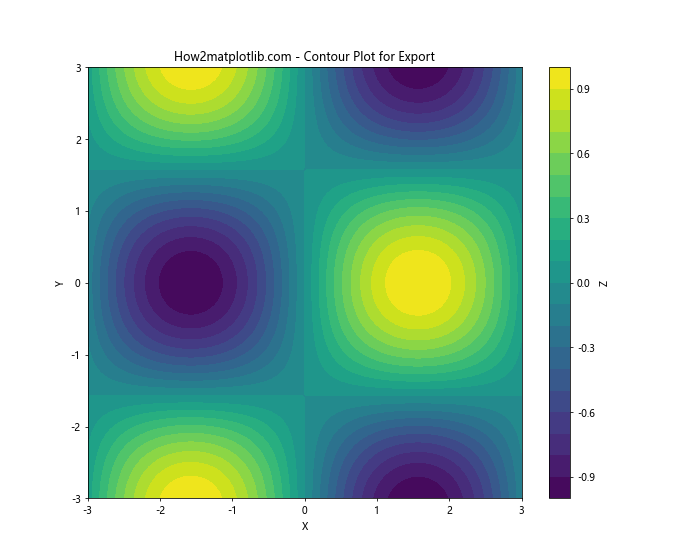
在这个例子中,我们将同一个等高线图保存为PNG、PDF和SVG三种不同的格式。PNG适合网页显示,PDF和SVG适合打印或进一步编辑。
结论
通过本文,我们详细探讨了如何使用Matplotlib绘制基于离散点的等高线图。我们从基本概念开始,逐步深入到更高级的技巧,包括自定义等高线、3D等高线图、动画、颜色映射、插值方法、性能优化、统计分析、误差分析、交互性以及图形的导出和保存。
等高线图是一种强大的数据可视化工具,可以帮助我们直观地理解三维数据的分布和变化趋势。通过掌握这些技巧,你将能够创建更加精美和信息丰富的等高线图,为你的数据分析和科学研究提供有力支持。
记住,创建优秀的等高线图不仅需要技术skills,还需要对数据有深入的理解。选择合适的参数、颜色映射和插值方法,可以帮助你更好地展示数据的特征和模式。同时,考虑到图形的受众,适当添加标签、注释和图例也是非常重要的。
 极客笔记
极客笔记