Matplotlib绘制简单矢量场:全面指南与实例
参考:How to plot a simple vector field in Matplotlib
矢量场是物理学、数学和工程学中的重要概念,它可以用来描述空间中每一点的方向和大小。在数据可视化中,矢量场的绘制能够直观地展示复杂的空间分布情况。Matplotlib作为Python中强大的绘图库,提供了丰富的工具来绘制矢量场。本文将详细介绍如何使用Matplotlib绘制简单的矢量场,并通过多个示例来展示不同的绘制技巧和方法。
1. 矢量场的基本概念
在开始绘制矢量场之前,我们需要理解什么是矢量场。矢量场是在空间中的每一点都定义了一个矢量的函数。在二维平面上,矢量场可以用箭头来表示,箭头的方向表示矢量的方向,箭头的长度表示矢量的大小。
以下是一个简单的矢量场示例:
import numpy as np
import matplotlib.pyplot as plt
# 创建网格点
x = np.linspace(-2, 2, 20)
y = np.linspace(-2, 2, 20)
X, Y = np.meshgrid(x, y)
# 定义矢量场函数
U = -Y
V = X
# 绘制矢量场
plt.figure(figsize=(8, 6))
plt.quiver(X, Y, U, V)
plt.title('Simple Vector Field - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
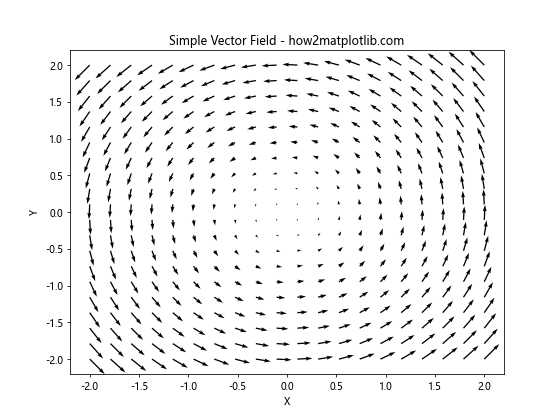
在这个例子中,我们创建了一个20×20的网格,并定义了一个简单的矢量场,其中U和V分别表示x和y方向上的分量。plt.quiver()函数用于绘制矢量场,它接受X和Y坐标以及对应的U和V分量作为参数。
2. Matplotlib中绘制矢量场的基本方法
Matplotlib提供了两个主要函数来绘制矢量场:quiver()和quiverkey()。
2.1 quiver()函数
quiver()函数是绘制矢量场的核心函数。它的基本语法如下:
plt.quiver(X, Y, U, V, **kwargs)
其中:
– X和Y是网格点的坐标
– U和V是对应点的矢量分量
– kwargs是可选参数,用于控制箭头的外观等
以下是一个使用quiver()函数的更复杂示例:
import numpy as np
import matplotlib.pyplot as plt
# 创建网格点
x = np.linspace(-3, 3, 30)
y = np.linspace(-3, 3, 30)
X, Y = np.meshgrid(x, y)
# 定义矢量场函数
U = X**2 - Y**2
V = 2*X*Y
# 计算矢量的大小
magnitude = np.sqrt(U**2 + V**2)
# 绘制矢量场
plt.figure(figsize=(10, 8))
q = plt.quiver(X, Y, U, V, magnitude, cmap='viridis', scale=50)
plt.colorbar(q)
plt.title('Complex Vector Field - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
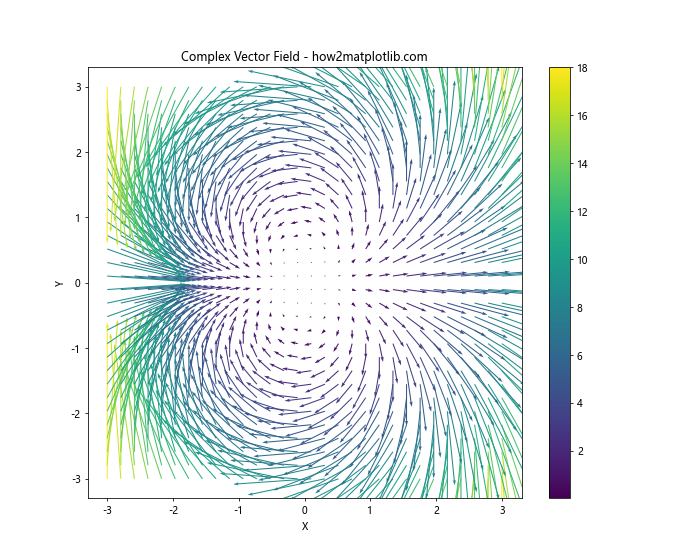
在这个例子中,我们定义了一个更复杂的矢量场,并使用矢量的大小来给箭头着色。scale参数用于控制箭头的长度,cmap参数指定了颜色映射。
2.2 quiverkey()函数
quiverkey()函数用于为矢量场添加图例。它的基本语法如下:
plt.quiverkey(Q, X, Y, U, label, **kwargs)
其中:
– Q是quiver()函数返回的对象
– X和Y是图例的位置
– U是图例箭头代表的大小
– label是图例的文本标签
以下是一个使用quiverkey()函数的示例:
import numpy as np
import matplotlib.pyplot as plt
# 创建网格点
x = np.linspace(-2, 2, 20)
y = np.linspace(-2, 2, 20)
X, Y = np.meshgrid(x, y)
# 定义矢量场函数
U = X
V = Y
# 绘制矢量场
plt.figure(figsize=(8, 6))
Q = plt.quiver(X, Y, U, V, scale=15)
plt.quiverkey(Q, X=0.85, Y=1.05, U=1, label='1 m/s', labelpos='E')
plt.title('Vector Field with Legend - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
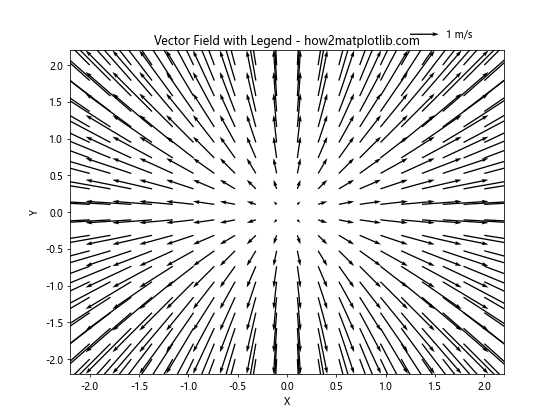
在这个例子中,我们添加了一个图例,表示箭头长度为1代表1 m/s的速度。
3. 自定义矢量场的外观
Matplotlib提供了多种方法来自定义矢量场的外观,包括箭头的颜色、大小、形状等。
3.1 调整箭头的颜色
我们可以使用color参数来设置箭头的颜色:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 2, 20)
y = np.linspace(-2, 2, 20)
X, Y = np.meshgrid(x, y)
U = -Y
V = X
plt.figure(figsize=(8, 6))
plt.quiver(X, Y, U, V, color='red')
plt.title('Red Vector Field - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
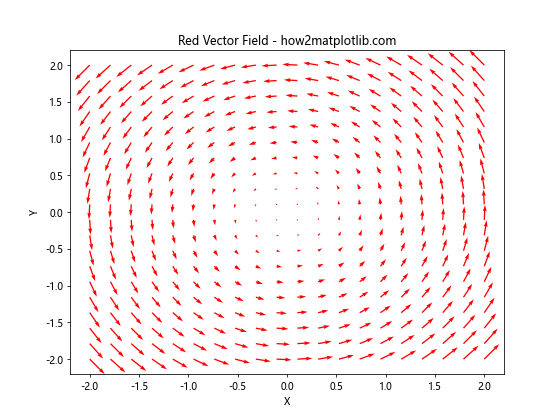
这个例子将所有箭头设置为红色。
3.2 根据矢量大小设置颜色
我们还可以根据矢量的大小来设置箭头的颜色:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 2, 20)
y = np.linspace(-2, 2, 20)
X, Y = np.meshgrid(x, y)
U = -Y
V = X
magnitude = np.sqrt(U**2 + V**2)
plt.figure(figsize=(8, 6))
q = plt.quiver(X, Y, U, V, magnitude, cmap='cool')
plt.colorbar(q)
plt.title('Color-coded Vector Field - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
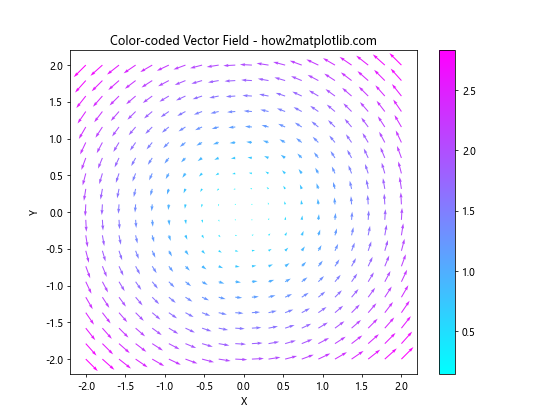
在这个例子中,箭头的颜色根据矢量的大小变化,使用了’cool’颜色映射。
3.3 调整箭头的大小和形状
我们可以使用scale、width和headwidth等参数来调整箭头的大小和形状:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 2, 10)
y = np.linspace(-2, 2, 10)
X, Y = np.meshgrid(x, y)
U = -Y
V = X
plt.figure(figsize=(8, 6))
plt.quiver(X, Y, U, V, scale=10, width=0.005, headwidth=5)
plt.title('Customized Arrow Shape - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
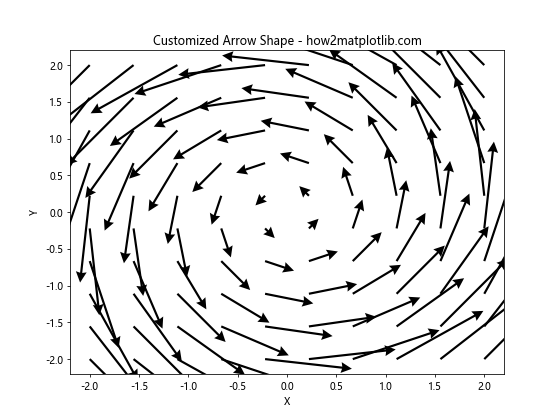
这个例子展示了如何调整箭头的大小和形状。
4. 绘制特殊类型的矢量场
除了基本的矢量场,Matplotlib还支持绘制一些特殊类型的矢量场,如流线图和极坐标矢量场。
4.1 绘制流线图
流线图是矢量场的另一种表示方式,它显示了场中的连续路径:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 2, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)
U = -Y
V = X
plt.figure(figsize=(8, 6))
plt.streamplot(X, Y, U, V, density=1, color='blue')
plt.title('Streamplot - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
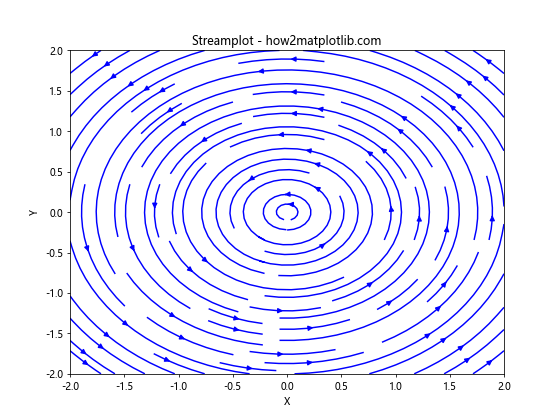
这个例子使用streamplot()函数绘制了流线图。
4.2 极坐标矢量场
我们还可以在极坐标系中绘制矢量场:
import numpy as np
import matplotlib.pyplot as plt
r = np.linspace(0, 2, 20)
theta = np.linspace(0, 2*np.pi, 20)
R, Theta = np.meshgrid(r, theta)
U = R * np.cos(Theta)
V = R * np.sin(Theta)
plt.figure(figsize=(8, 8))
ax = plt.subplot(111, projection='polar')
ax.quiver(Theta, R, U, V)
plt.title('Polar Vector Field - how2matplotlib.com')
plt.show()
Output:
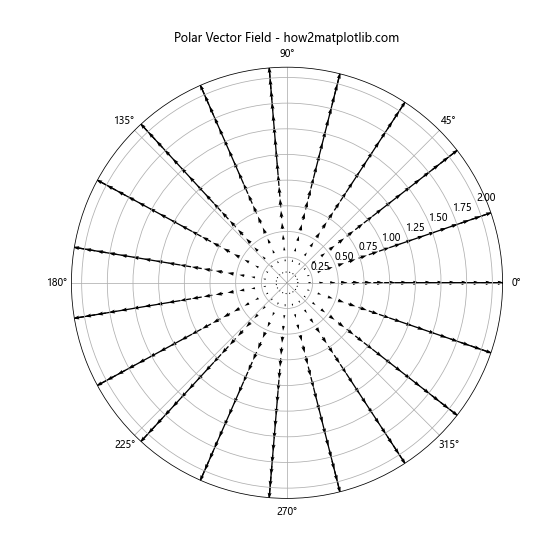
这个例子展示了如何在极坐标系中绘制矢量场。
5. 结合等高线图和矢量场
有时,将矢量场与等高线图结合可以提供更多信息:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 2, 30)
y = np.linspace(-2, 2, 30)
X, Y = np.meshgrid(x, y)
U = -Y
V = X
Z = X**2 + Y**2
plt.figure(figsize=(10, 8))
plt.contourf(X, Y, Z, cmap='viridis', alpha=0.5)
plt.quiver(X, Y, U, V, color='white')
plt.colorbar(label='Z value')
plt.title('Vector Field with Contour Plot - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
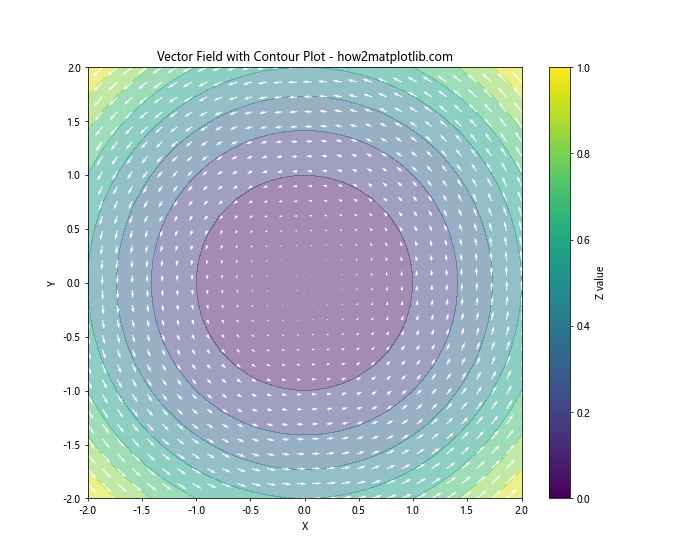
这个例子展示了如何将矢量场与等高线图结合。
6. 3D矢量场
Matplotlib还支持绘制3D矢量场:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x = np.linspace(-2, 2, 10)
y = np.linspace(-2, 2, 10)
z = np.linspace(-2, 2, 10)
X, Y, Z = np.meshgrid(x, y, z)
U = -Y
V = X
W = Z
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.quiver(X, Y, Z, U, V, W, length=0.1, normalize=True)
ax.set_title('3D Vector Field - how2matplotlib.com')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
Output:
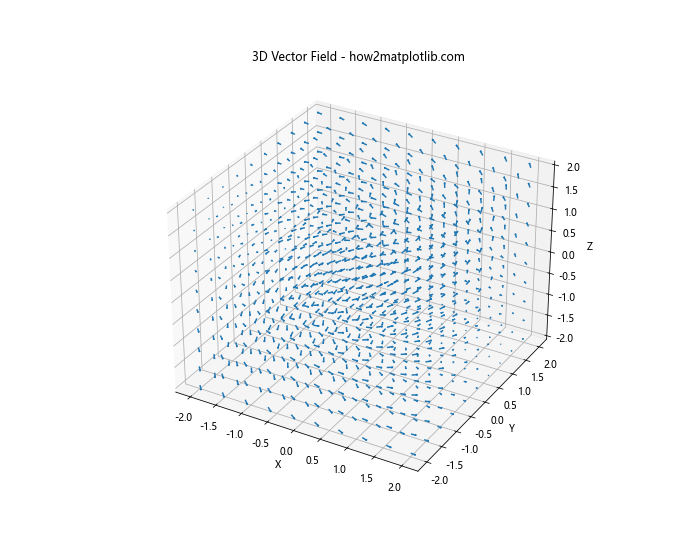
这个例子展示了如何绘制3D矢量场。
7. 动画矢量场
我们还可以创建动画矢量场来展示随时间变化的情况:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
x = np.linspace(-2, 2, 20)
y = np.linspace(-2, 2, 20)
X, Y = np.meshgrid(x, y)
fig, ax = plt.subplots(figsize=(8, 6))
Q = ax.quiver(X, Y, np.zeros_like(X), np.zeros_like(Y))
ax.set_title('Animated Vector Field - how2matplotlib.com')
ax.set_xlabel('X')
ax.set_ylabel('Y')
def update(frame):
U = -Y * np.cos(frame)
V = X * np.sin(frame)
Q.set_UVC(U, V)
return Q,
anim = FuncAnimation(fig, update, frames=np.linspace(0, 2*np.pi, 100), interval=50, blit=True)
plt.show()
Output:
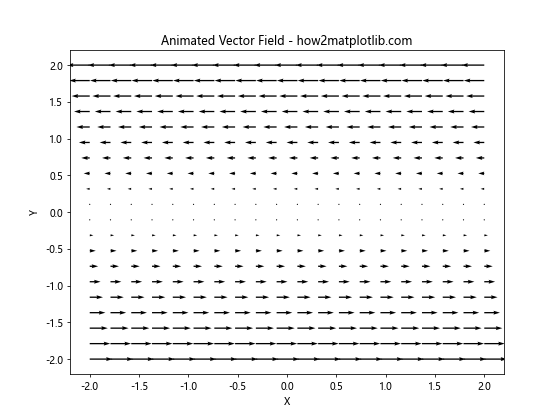
这个例子创建了一个随时间变化的动画矢量场。
8. 高级技巧:矢量场插值
有时,我们可能需要对稀疏的矢量场数据进行插值,以获得更平滑的可视化效果:
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import griddata
# 创建稀疏数据
x = np.random.rand(50) * 4 - 2
y = np.random.rand(50) * 4 - 2
u = -y
v = x
# 创建网格
xi = np.linspace(-2, 2, 30)
yi = np.linspace(-2, 2, 30)
X, Y = np.meshgrid(xi, yi)
# 插值
U = griddata((x, y), u, (X, Y), method='cubic')
V = griddata((x, y), v, (X, Y), method='cubic')
plt.figure(figsize=(10, 8))
plt.quiver(X, Y, U, V)
plt.scatter(x, y, color='red', s=10)
plt.title('Interpolated Vector Field - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
Output:
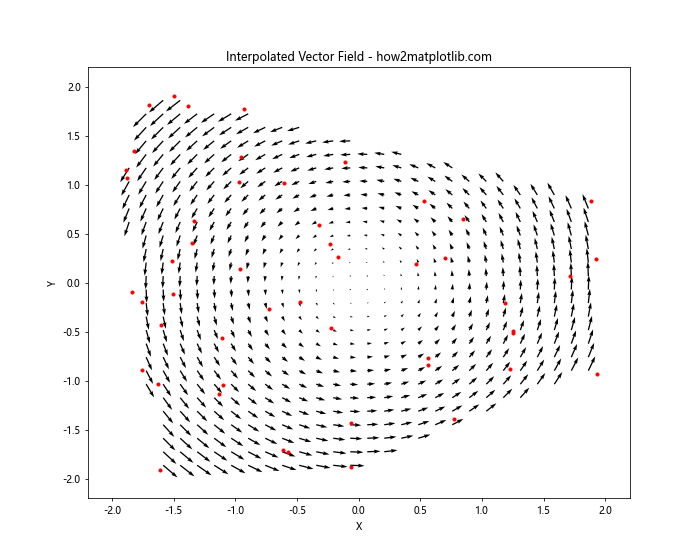
这个例子展示了如何对稀疏的矢量场数据进行插值,并绘制结果。
9. 结合其他可视化技术
矢量场可以与其他可视化技术结合,以提供更丰富的信息:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 2, 20)
y = np.linspace(-2, 2, 20)
X, Y = np.meshgrid(x, y)
U = -Y
V = X
speed = np.sqrt(U**2 + V**2)
plt.figure(figsize=(12, 8))
# 绘制背景热图
plt.pcolormesh(X, Y, speed, cmap='viridis', shading='auto')
plt.colorbar(label='Speed')
# 绘制矢量场
plt.quiver(X, Y, U, V, color='white', alpha=0.8)
# 添加一些流线
plt.streamplot(X, Y, U, V, color='red', linewidth=1, density=0.5, arrowsize=1)
plt.title('Combined Visualization Techniques - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
这个例子展示了如何将矢量场、热图和流线图结合在一起,提供了一个更全面的可视化效果。
10. 处理大规模矢量场数据
当处理大规模矢量场数据时,直接绘制所有箭头可能会导致图像过于拥挤。在这种情况下,我们可以采用一些策略来优化可视化效果:
10.1 降采样
一种简单的方法是对数据进行降采样:
import numpy as np
import matplotlib.pyplot as plt
# 创建大规模数据
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
U = -Y
V = X
# 降采样
step = 5
X_sampled = X[::step, ::step]
Y_sampled = Y[::step, ::step]
U_sampled = U[::step, ::step]
V_sampled = V[::step, ::step]
plt.figure(figsize=(10, 8))
plt.quiver(X_sampled, Y_sampled, U_sampled, V_sampled)
plt.title('Downsampled Vector Field - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
这个例子展示了如何通过降采样来处理大规模矢量场数据。
10.2 使用pivot参数
quiver()函数的pivot参数可以用来控制箭头的锚点位置,这在处理密集数据时很有用:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-5, 5, 50)
y = np.linspace(-5, 5, 50)
X, Y = np.meshgrid(x, y)
U = -Y
V = X
plt.figure(figsize=(15, 5))
# 默认pivot
plt.subplot(131)
plt.quiver(X, Y, U, V)
plt.title('Default Pivot - how2matplotlib.com')
# pivot='mid'
plt.subplot(132)
plt.quiver(X, Y, U, V, pivot='mid')
plt.title('Pivot: Mid - how2matplotlib.com')
# pivot='tip'
plt.subplot(133)
plt.quiver(X, Y, U, V, pivot='tip')
plt.title('Pivot: Tip - how2matplotlib.com')
plt.tight_layout()
plt.show()
这个例子展示了不同pivot值对矢量场可视化的影响。
11. 自定义矢量场函数
有时,我们可能需要绘制由特定函数定义的矢量场。以下是一个例子,展示了如何绘制由复杂函数定义的矢量场:
import numpy as np
import matplotlib.pyplot as plt
def vector_field(x, y):
return np.sin(x) * np.cos(y), np.cos(x) * np.sin(y)
x = np.linspace(-np.pi, np.pi, 30)
y = np.linspace(-np.pi, np.pi, 30)
X, Y = np.meshgrid(x, y)
U, V = vector_field(X, Y)
plt.figure(figsize=(10, 8))
plt.quiver(X, Y, U, V)
plt.title('Custom Vector Field Function - how2matplotlib.com')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
这个例子展示了如何使用自定义函数来定义和绘制矢量场。
12. 矢量场的数学分析
矢量场的可视化不仅可以用于展示数据,还可以用于数学分析。例如,我们可以计算和可视化矢量场的散度和旋度:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 2, 30)
y = np.linspace(-2, 2, 30)
X, Y = np.meshgrid(x, y)
U = X**2 - Y**2
V = 2*X*Y
# 计算散度
div = np.gradient(U, x, axis=1) + np.gradient(V, y, axis=0)
# 计算旋度(在2D中,旋度是标量)
curl = np.gradient(V, x, axis=1) - np.gradient(U, y, axis=0)
plt.figure(figsize=(15, 5))
# 原始矢量场
plt.subplot(131)
plt.quiver(X, Y, U, V)
plt.title('Original Field - how2matplotlib.com')
# 散度
plt.subplot(132)
plt.contourf(X, Y, div, cmap='RdBu')
plt.colorbar(label='Divergence')
plt.title('Divergence - how2matplotlib.com')
# 旋度
plt.subplot(133)
plt.contourf(X, Y, curl, cmap='RdBu')
plt.colorbar(label='Curl')
plt.title('Curl - how2matplotlib.com')
plt.tight_layout()
plt.show()
这个例子展示了如何计算和可视化矢量场的散度和旋度。
13. 矢量场在实际应用中的可视化
矢量场在许多实际应用中都有重要作用。以下是一个简化的风场可视化示例:
import numpy as np
import matplotlib.pyplot as plt
def wind_field(x, y):
return y * np.sin(x), -x * np.cos(y)
x = np.linspace(-5, 5, 40)
y = np.linspace(-5, 5, 40)
X, Y = np.meshgrid(x, y)
U, V = wind_field(X, Y)
speed = np.sqrt(U**2 + V**2)
plt.figure(figsize=(12, 9))
# 背景颜色表示风速
plt.contourf(X, Y, speed, cmap='YlOrRd')
plt.colorbar(label='Wind Speed')
# 箭头表示风向
plt.quiver(X, Y, U, V, scale=50)
plt.title('Simplified Wind Field Visualization - how2matplotlib.com')
plt.xlabel('Longitude')
plt.ylabel('Latitude')
plt.show()
这个例子展示了如何使用矢量场来可视化风场,其中箭头表示风向,背景颜色表示风速。
14. 结合地理信息的矢量场可视化
在地理信息系统(GIS)中,矢量场可视化常常需要结合地理背景。以下是一个简化的例子,展示如何在地图背景上绘制矢量场:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.basemap import Basemap
def ocean_current(lon, lat):
return np.sin(lat) * np.cos(lon), np.cos(lat) * np.sin(lon)
# 创建地图
m = Basemap(projection='mill', llcrnrlat=-60, urcrnrlat=60,
llcrnrlon=-180, urcrnrlon=180, resolution='c')
# 创建经纬度网格
lon = np.linspace(-180, 180, 60)
lat = np.linspace(-60, 60, 40)
LON, LAT = np.meshgrid(lon, lat)
# 计算海流
U, V = ocean_current(np.radians(LON), np.radians(LAT))
# 绘制地图
plt.figure(figsize=(15, 10))
m.drawcoastlines()
m.fillcontinents(color='lightgray', lake_color='aqua')
m.drawparallels(np.arange(-60, 61, 30), labels=[1, 0, 0, 0])
m.drawmeridians(np.arange(-180, 181, 60), labels=[0, 0, 0, 1])
# 绘制海流
x, y = m(LON, LAT)
m.quiver(x, y, U, V, scale=50, alpha=0.5)
plt.title('Simplified Ocean Current Visualization - how2matplotlib.com')
plt.show()
这个例子展示了如何在世界地图上绘制简化的海洋洋流矢量场。注意,这需要安装basemap库。
15. 总结
通过本文的详细介绍和多个示例,我们全面探讨了如何使用Matplotlib绘制简单的矢量场。从基本概念到高级技巧,我们涵盖了以下主要内容:
- 矢量场的基本概念和Matplotlib中的基本绘制方法
- 自定义矢量场的外观,包括颜色、大小和形状
- 特殊类型的矢量场,如流线图和极坐标矢量场
- 结合其他可视化技术,如等高线图和热图
- 3D矢量场的绘制
- 动画矢量场的创建
- 处理大规模矢量场数据的策略
- 自定义矢量场函数的使用
- 矢量场的数学分析,如散度和旋度的可视化
- 矢量场在实际应用中的可视化,如风场和海洋洋流
通过这些内容,读者应该能够掌握使用Matplotlib绘制各种类型矢量场的技能,并能够根据具体需求进行自定义和优化。矢量场可视化是一个强大的工具,可以帮助我们理解和分析复杂的空间数据,在科学研究、工程应用和数据分析等多个领域都有广泛的应用。
 极客笔记
极客笔记