当前位置：极客笔记 > Matplotlib > Matplotlib 问答 > 如何使用Python的Matplotlib绘制正态分布图

如何使用Python的Matplotlib绘制正态分布图

如何使用Python的Matplotlib绘制正态分布图

参考：How to plot a normal distribution with Matplotlib in Python

正态分布，也称为高斯分布，是统计学和概率论中最重要的概率分布之一。在数据分析和可视化中，能够绘制正态分布图是一项非常有用的技能。本文将详细介绍如何使用Python的Matplotlib库来绘制正态分布图，包括基本的正态分布图、自定义参数的正态分布图、多个正态分布的对比图等多种情况。我们将通过多个示例来展示Matplotlib的强大功能，帮助读者掌握绘制正态分布图的各种技巧。

1. 基本的正态分布图

首先，让我们从最基本的正态分布图开始。我们将使用NumPy库生成正态分布的数据，然后使用Matplotlib绘制直方图和概率密度函数（PDF）曲线。

import numpy as np
import matplotlib.pyplot as plt

# 生成正态分布数据
mu, sigma = 0, 1  # 均值和标准差
data = np.random.normal(mu, sigma, 1000)

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制直方图
ax.hist(data, bins=30, density=True, alpha=0.7, color='skyblue', edgecolor='black')

# 生成用于绘制PDF的x值
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 100)

# 计算PDF
pdf = (1 / (sigma * np.sqrt(2 * np.pi))) * np.exp(-(x - mu)**2 / (2 * sigma**2))

# 绘制PDF曲线
ax.plot(x, pdf, 'r-', lw=2, label='Normal PDF')

# 设置标题和标签
ax.set_title('Normal Distribution (how2matplotlib.com)', fontsize=16)
ax.set_xlabel('Value', fontsize=12)
ax.set_ylabel('Density', fontsize=12)

# 添加图例
ax.legend(fontsize=10)

# 显示网格
ax.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

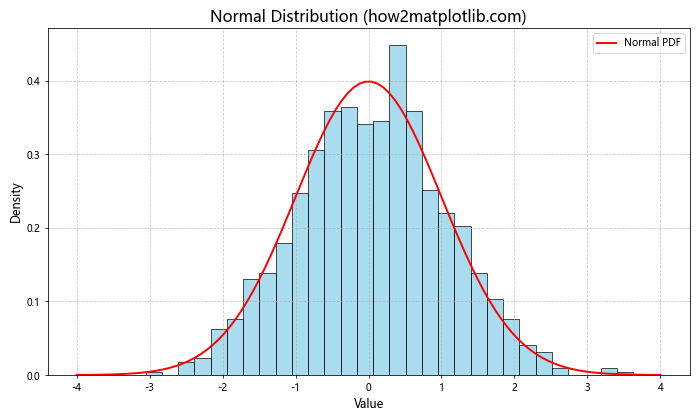
在这个示例中，我们首先使用np.random.normal()生成了1000个服从正态分布的随机数。然后，我们创建了一个图形和坐标轴，使用ax.hist()绘制了数据的直方图。接下来，我们计算了理论上的概率密度函数（PDF），并使用ax.plot()绘制了PDF曲线。最后，我们添加了标题、标签和图例，并显示了网格线以增强可读性。

2. 自定义参数的正态分布图

在实际应用中，我们可能需要绘制具有不同均值和标准差的正态分布图。下面的示例展示了如何绘制三个不同参数的正态分布图。

import numpy as np
import matplotlib.pyplot as plt

# 定义三组不同的均值和标准差
params = [(0, 1), (2, 1.5), (-1, 0.5)]
colors = ['blue', 'green', 'red']

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(12, 7))

# 为每组参数绘制正态分布
for (mu, sigma), color in zip(params, colors):
    # 生成x值
    x = np.linspace(mu - 4*sigma, mu + 4*sigma, 100)

    # 计算PDF
    pdf = (1 / (sigma * np.sqrt(2 * np.pi))) * np.exp(-(x - mu)**2 / (2 * sigma**2))

    # 绘制PDF曲线
    ax.plot(x, pdf, color=color, lw=2, label=f'μ={mu}, σ={sigma}')

# 设置标题和标签
ax.set_title('Multiple Normal Distributions (how2matplotlib.com)', fontsize=16)
ax.set_xlabel('Value', fontsize=12)
ax.set_ylabel('Density', fontsize=12)

# 添加图例
ax.legend(fontsize=10)

# 显示网格
ax.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

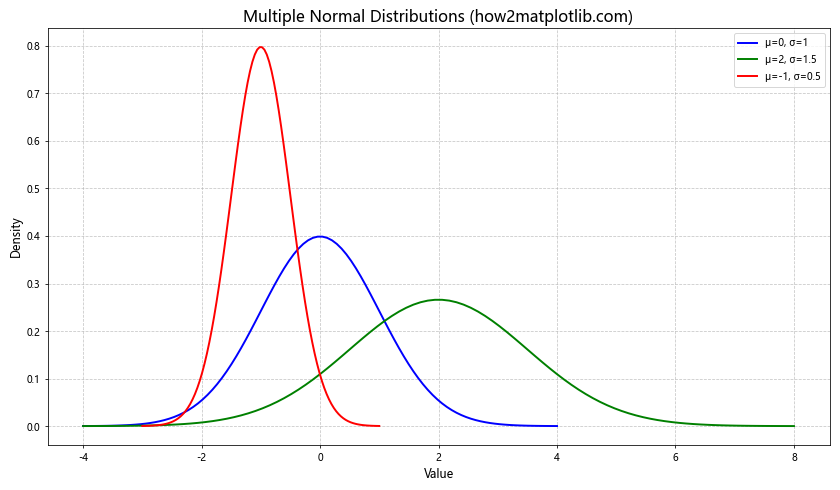
在这个示例中，我们定义了三组不同的均值和标准差参数。我们使用循环为每组参数计算并绘制了相应的PDF曲线。通过使用不同的颜色和标签，我们可以清楚地区分不同的正态分布。

3. 累积分布函数（CDF）的绘制

除了概率密度函数，累积分布函数（CDF）也是描述正态分布的重要工具。以下示例展示了如何绘制正态分布的CDF。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(10, 6))

# 生成x值
x = np.linspace(-4, 4, 100)

# 计算CDF
cdf = norm.cdf(x)

# 绘制CDF曲线
ax.plot(x, cdf, 'b-', lw=2, label='Normal CDF')

# 设置标题和标签
ax.set_title('Cumulative Distribution Function (how2matplotlib.com)', fontsize=16)
ax.set_xlabel('Value', fontsize=12)
ax.set_ylabel('Cumulative Probability', fontsize=12)

# 添加图例
ax.legend(fontsize=10)

# 显示网格
ax.grid(True, linestyle='--', alpha=0.7)

# 设置y轴范围
ax.set_ylim(0, 1.1)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

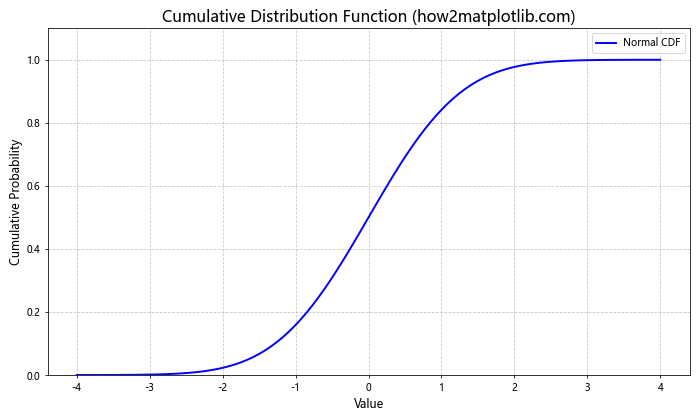
在这个示例中，我们使用了SciPy库的norm.cdf()函数来计算正态分布的累积分布函数。CDF表示随机变量小于或等于某个值的概率，因此y轴的范围被设置为0到1。

4. Q-Q图（Quantile-Quantile Plot）

Q-Q图是用于比较两个概率分布的图形方法，特别适用于检验数据是否服从正态分布。以下示例展示了如何使用Matplotlib绘制Q-Q图。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 生成正态分布数据
np.random.seed(42)
data = np.random.normal(0, 1, 1000)

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(10, 10))

# 绘制Q-Q图
stats.probplot(data, dist="norm", plot=ax)

# 设置标题和标签
ax.set_title('Q-Q Plot (how2matplotlib.com)', fontsize=16)
ax.set_xlabel('Theoretical Quantiles', fontsize=12)
ax.set_ylabel('Sample Quantiles', fontsize=12)

# 显示网格
ax.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

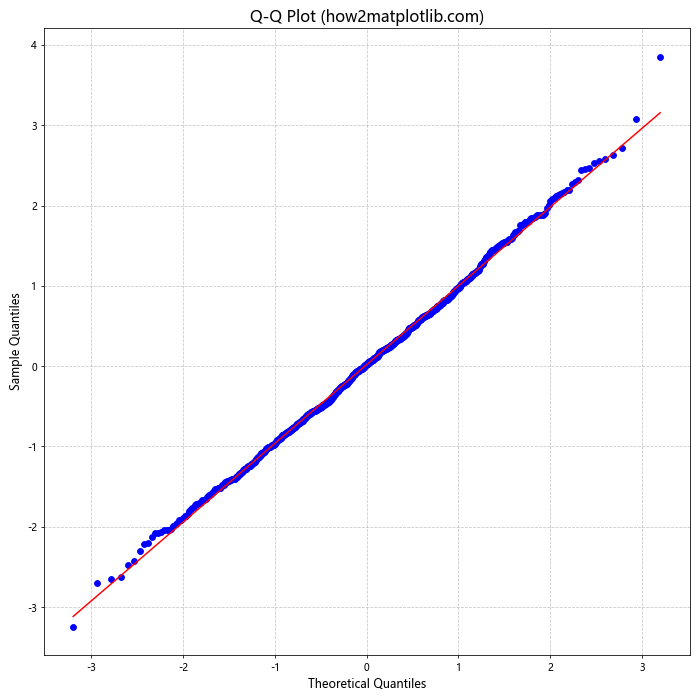
在这个示例中，我们使用SciPy的stats.probplot()函数来生成Q-Q图。如果数据点大致落在对角线上，则表明数据近似服从正态分布。

5. 3D正态分布图

Matplotlib还支持绘制3D图形，我们可以用它来可视化二维正态分布。以下示例展示了如何创建3D正态分布图。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建网格点
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)

# 计算Z值（概率密度）
Z = (1 / (2 * np.pi)) * np.exp(-0.5 * (X**2 + Y**2))

# 创建3D图形
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制3D表面
surf = ax.plot_surface(X, Y, Z, cmap='viridis')

# 设置标题和标签
ax.set_title('3D Normal Distribution (how2matplotlib.com)', fontsize=16)
ax.set_xlabel('X', fontsize=12)
ax.set_ylabel('Y', fontsize=12)
ax.set_zlabel('Density', fontsize=12)

# 添加颜色条
fig.colorbar(surf, shrink=0.5, aspect=5)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

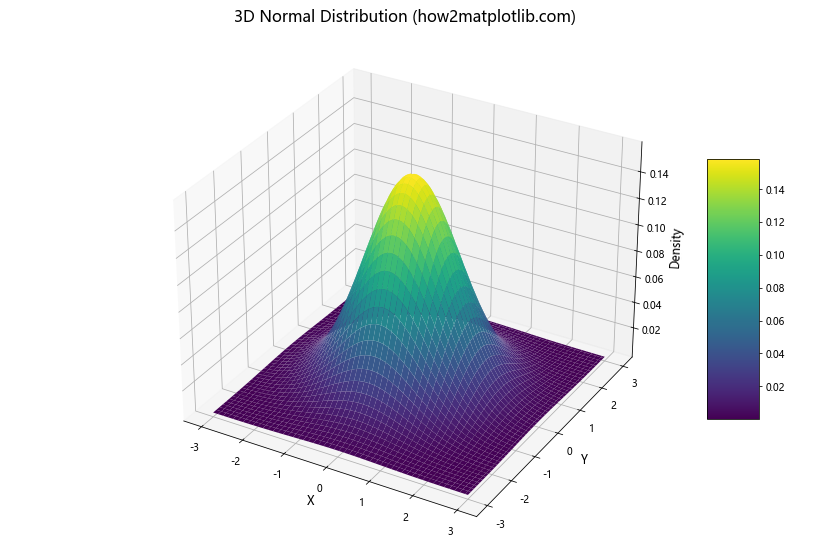
在这个示例中，我们使用np.meshgrid()创建了一个二维网格，然后计算了每个网格点上的概率密度。使用ax.plot_surface()函数，我们绘制了一个3D表面图，展示了二维正态分布的形状。

6. 正态分布的置信区间

在统计分析中，置信区间是一个重要的概念。以下示例展示了如何在正态分布图上标注置信区间。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 设置参数
mu, sigma = 0, 1
confidence_level = 0.95

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(12, 6))

# 生成x值
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 100)

# 计算PDF
pdf = stats.norm.pdf(x, mu, sigma)

# 绘制PDF曲线
ax.plot(x, pdf, 'b-', lw=2, label='Normal PDF')

# 计算置信区间
ci = stats.norm.interval(confidence_level, mu, sigma)

# 填充置信区间
ax.fill_between(x, pdf, where=(x >= ci[0]) & (x <= ci[1]), color='skyblue', alpha=0.5, 
                label=f'{confidence_level*100:.0f}% Confidence Interval')

# 设置标题和标签
ax.set_title('Normal Distribution with Confidence Interval (how2matplotlib.com)', fontsize=16)
ax.set_xlabel('Value', fontsize=12)
ax.set_ylabel('Density', fontsize=12)

# 添加图例
ax.legend(fontsize=10)

# 显示网格
ax.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

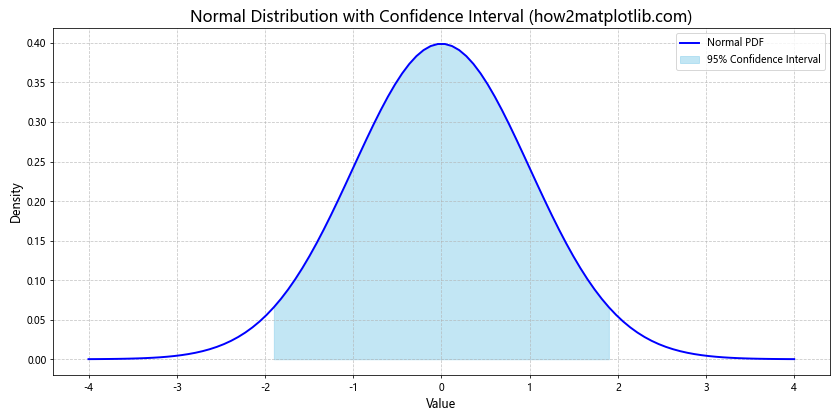
在这个示例中，我们使用stats.norm.interval()函数计算了95%的置信区间，然后使用ax.fill_between()函数在图上填充了这个区间。这种可视化方法可以直观地展示数据的分布和不确定性。

7. 正态分布的概率计算

Matplotlib不仅可以用于绘图，还可以与其他库结合使用来进行概率计算和可视化。以下示例展示了如何计算并可视化正态分布中特定区间的概率。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 设置参数
mu, sigma = 0, 1
lower_bound, upper_bound = -1, 1

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(12, 6))

# 生成x值
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 1000)

# 计算PDF
pdf = stats.norm.pdf(x, mu, sigma)

# 绘制PDF曲线
ax.plot(x, pdf, 'b-', lw=2, label='Normal PDF')

# 填充指定区间
x_fill = np.linspace(lower_bound, upper_bound, 100)
ax.fill_between(x_fill, stats.norm.pdf(x_fill, mu, sigma), color='skyblue', alpha=0.5)

# 计算概率
probability = stats.norm.cdf(upper_bound, mu, sigma) - stats.norm.cdf(lower_bound, mu, sigma)

# 设置标题和标签
ax.set_title(f'Probability between {lower_bound} and {upper_bound}: {probability:.4f} (how2matplotlib.com)', fontsize=16)
ax.set_xlabel('Value', fontsize=12)
ax.set_ylabel('Density', fontsize=12)

# 添加图例
ax.legend(fontsize=10)

# 显示网格
ax.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

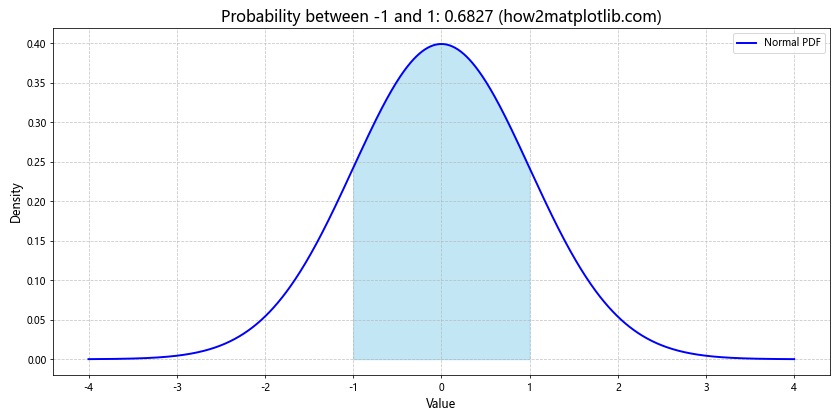
在这个示例中，我们计算并可视化了正态分布中-1到1之间的概率。我们使用stats.norm.cdf()函数计算累积概率，然后用ax.fill_between()函数填充相应的区域。这种方法可以直观地展示特定区间的概率。

8. 正态分布的比较

在某些情况下，我们可能需要比较多个正态分布。以下示例展示了如何在同一图表中比较多个正态分布，并使用不同的线型和颜色来区分它们。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 定义多个正态分布的参数
distributions = [
    {'mu': 0, 'sigma': 1, 'color': 'blue', 'label': 'Standard Normal'},
    {'mu': 1, 'sigma': 1.5, 'color': 'red', 'label': 'Shifted and Wider'},
    {'mu': -1, 'sigma': 0.5, 'color': 'green', 'label': 'Shifted and Narrower'}
]

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(12, 6))

# 生成x值
x = np.linspace(-5,5, 1000)

# 绘制每个分布
for dist in distributions:
    pdf = stats.norm.pdf(x, dist['mu'], dist['sigma'])
    ax.plot(x, pdf, color=dist['color'], lw=2, label=dist['label'])

# 设置标题和标签
ax.set_title('Comparison of Normal Distributions (how2matplotlib.com)', fontsize=16)
ax.set_xlabel('Value', fontsize=12)
ax.set_ylabel('Density', fontsize=12)

# 添加图例
ax.legend(fontsize=10)

# 显示网格
ax.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

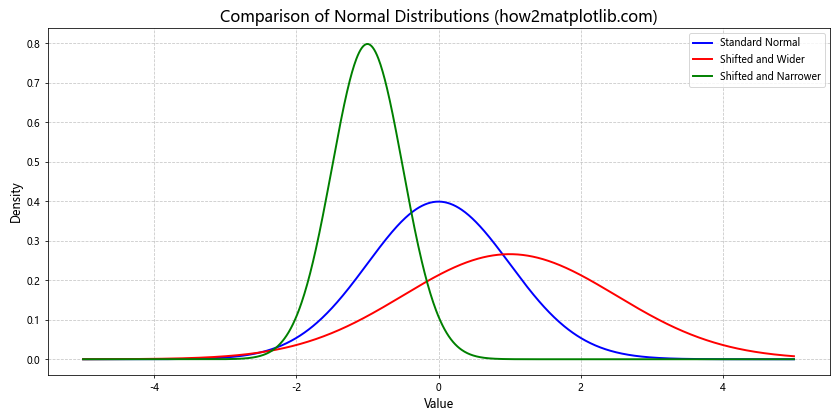
在这个示例中，我们定义了三个不同的正态分布，每个分布都有自己的均值、标准差、颜色和标签。我们使用循环来绘制每个分布的PDF曲线，这样可以方便地比较它们的形状和位置。

9. 正态分布的箱线图

箱线图是另一种用于可视化数据分布的有效工具。以下示例展示了如何为正态分布数据创建箱线图。

import numpy as np
import matplotlib.pyplot as plt

# 生成正态分布数据
np.random.seed(42)
data = np.random.normal(0, 1, 1000)

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制箱线图
ax.boxplot(data, vert=False)

# 设置标题和标签
ax.set_title('Box Plot of Normal Distribution (how2matplotlib.com)', fontsize=16)
ax.set_xlabel('Value', fontsize=12)
ax.set_ylabel('Distribution', fontsize=12)

# 显示网格
ax.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

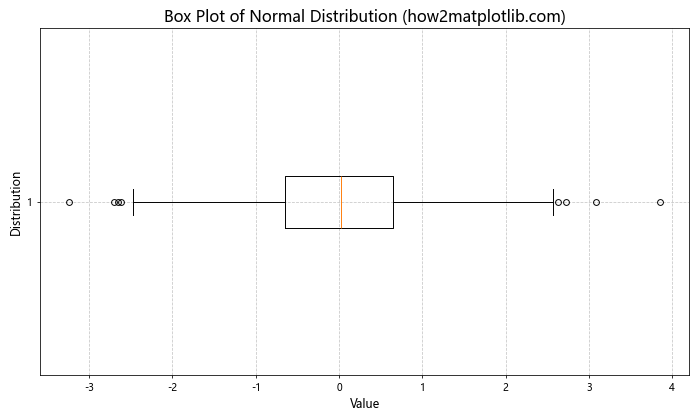
在这个示例中，我们使用ax.boxplot()函数创建了一个水平的箱线图。箱线图显示了数据的中位数、四分位数范围和异常值，提供了数据分布的快速概览。

10. 正态分布的核密度估计

核密度估计（KDE）是一种非参数方法，用于估计随机变量的概率密度函数。以下示例展示了如何使用KDE来可视化正态分布数据。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 生成正态分布数据
np.random.seed(42)
data = np.random.normal(0, 1, 1000)

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(12, 6))

# 绘制直方图
ax.hist(data, bins=30, density=True, alpha=0.7, color='skyblue', edgecolor='black')

# 计算KDE
kde = stats.gaussian_kde(data)
x_range = np.linspace(data.min(), data.max(), 100)
ax.plot(x_range, kde(x_range), 'r-', lw=2, label='KDE')

# 绘制真实的PDF
true_pdf = stats.norm.pdf(x_range, 0, 1)
ax.plot(x_range, true_pdf, 'g--', lw=2, label='True PDF')

# 设置标题和标签
ax.set_title('Kernel Density Estimation vs True PDF (how2matplotlib.com)', fontsize=16)
ax.set_xlabel('Value', fontsize=12)
ax.set_ylabel('Density', fontsize=12)

# 添加图例
ax.legend(fontsize=10)

# 显示网格
ax.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

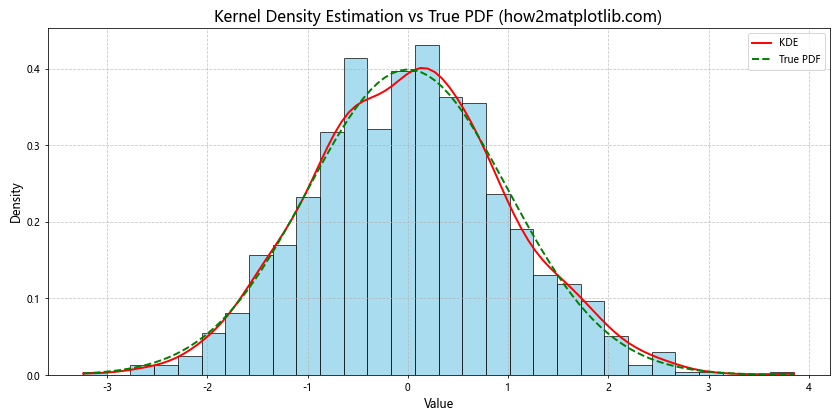
在这个示例中，我们首先绘制了数据的直方图，然后使用stats.gaussian_kde()函数计算了KDE。我们还绘制了真实的PDF曲线以进行比较。这种方法可以帮助我们了解KDE如何近似真实的概率密度函数。

11. 正态分布的残差图

在回归分析中，残差图是一个重要的诊断工具。以下示例展示了如何创建一个模拟的残差图，假设残差服从正态分布。

import numpy as np
import matplotlib.pyplot as plt

# 生成模拟数据
np.random.seed(42)
x = np.linspace(0, 10, 100)
y = 2 * x + 1 + np.random.normal(0, 1, 100)

# 拟合线性模型
coeffs = np.polyfit(x, y, 1)
y_fit = np.polyval(coeffs, x)

# 计算残差
residuals = y - y_fit

# 创建图形和坐标轴
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10), sharex=True)

# 绘制散点图和拟合线
ax1.scatter(x, y, alpha=0.7)
ax1.plot(x, y_fit, 'r-', lw=2)
ax1.set_title('Linear Regression (how2matplotlib.com)', fontsize=16)
ax1.set_ylabel('Y', fontsize=12)

# 绘制残差图
ax2.scatter(x, residuals, alpha=0.7)
ax2.axhline(y=0, color='r', linestyle='--')
ax2.set_title('Residual Plot', fontsize=16)
ax2.set_xlabel('X', fontsize=12)
ax2.set_ylabel('Residuals', fontsize=12)

# 显示网格
ax1.grid(True, linestyle='--', alpha=0.7)
ax2.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

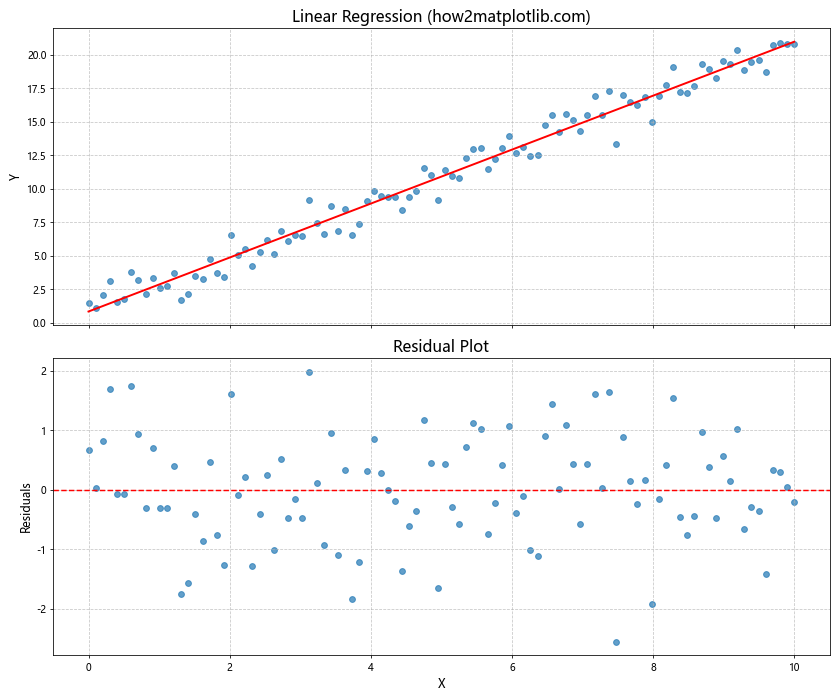
在这个示例中，我们首先生成了一些模拟数据并拟合了一个线性模型。然后，我们计算了残差并创建了两个子图：一个显示原始数据和拟合线，另一个显示残差。如果残差呈现随机分布且大致对称分布在零线周围，这通常表明模型拟合得较好。

12. 正态分布的概率图

概率图是另一种用于检验数据是否服从正态分布的图形方法。以下示例展示了如何创建正态概率图。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 生成正态分布数据
np.random.seed(42)
data = np.random.normal(0, 1, 1000)

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(10, 10))

# 创建概率图
stats.probplot(data, dist="norm", plot=ax)

# 设置标题和标签
ax.set_title('Normal Probability Plot (how2matplotlib.com)', fontsize=16)
ax.set_xlabel('Theoretical Quantiles', fontsize=12)
ax.set_ylabel('Sample Quantiles', fontsize=12)

# 显示网格
ax.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

Output:

如何使用Python的Matplotlib绘制正态分布图

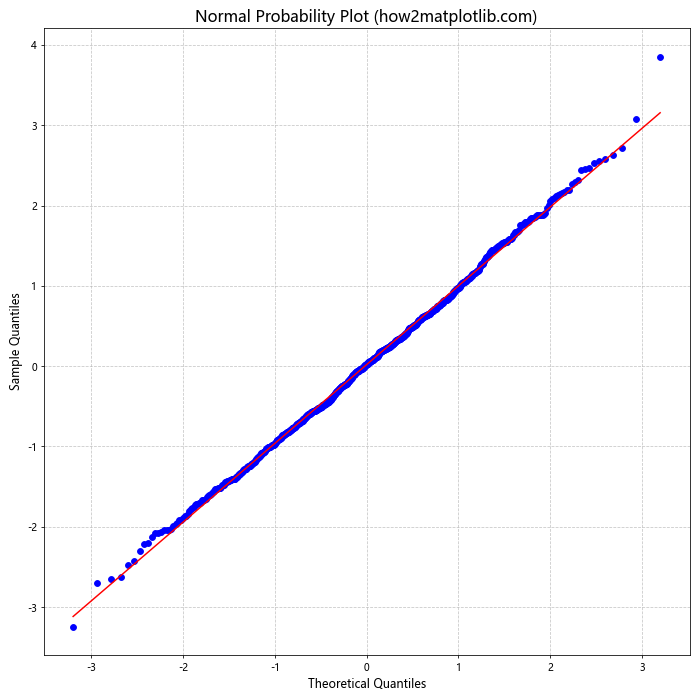
在这个示例中，我们使用stats.probplot()函数创建了一个正态概率图。如果数据点大致落在对角线上，则表明数据近似服从正态分布。这种图形可以帮助我们识别数据中的非正态性或异常值。

结论

通过本文的详细介绍和多个示例，我们展示了如何使用Python的Matplotlib库来绘制各种类型的正态分布图。从基本的概率密度函数和累积分布函数，到更高级的3D图形、置信区间和概率计算，我们涵盖了多个方面。这些技巧不仅适用于正态分布，还可以应用于其他类型的概率分布。

掌握这些可视化技巧对于数据分析、统计学习和机器学习都非常有帮助。通过合适的可视化，我们可以更好地理解数据的分布特征，发现潜在的模式和异常，并为进一步的分析提供直观的指导。

Camera课程

Camera API2 教程

API2 教程
Camera 性能教程

Perf 教程
Camera Native Framework 教程

Native FW 教程
Camera QCOM ISP 教程

ISP 教程
Camera QCOM Sensor 教程

Sensor 教程

Python教程

Python 教程

Python 教程
NumPy 教程

NumPy 教程
Django 教程

Django 教程

Java教程

Java 教程

Java 教程

Web教程

JavaScript 教程

JavaScript 教程
jQuery 教程

jQuery 教程
CSS 教程

CSS 教程
PHP 教程

PHP 教程
Laravel 教程

Laravel 教程
TypeScript 教程

TypeScript 教程
WordPress 教程

WordPress 教程

数据库教程

SQL 教程

SQL 教程
SQLite 教程

SQLite 教程
MySQL 教程

MySQL 教程
PL/SQL 教程

PL/SQL 教程
MongoDB 教程

MongoDB 教程

图形图像教程

OpenCV 教程

OpenCV 教程

办公软件教程

Excel 教程

Excel 教程

Linux教程

Linux命令全集

Linux命令全集
Linux内核API

Linux内核API
LVGL 教程

LVGL 教程

计算机教程

操作系统 教程

操作系统 教程
计算机网络 教程

计算机网络 教程
C语言 教程

C语言 教程
C++ 教程

C++ 教程
Swift 教程

Swift 教程

大数据教程

Hadoop 教程

Hadoop 教程
Spark 教程

Spark 教程
Scala 教程

Scala 教程

开发工具教程

Git 教程

Git 教程
Jenkins 教程

Jenkins 教程
ChatGPT 教程

ChatGPT 教程
IntelliJ 教程

IntelliJ 教程