前面学习了规则图形的填充,可以解决大部分问题了,但是有时候需要进行不规则图形的填充,或者两条曲线相交的部分进行填充,就需要使用另外的方法来解决了,再采用前面用列表的方式来表示点,已经不满足要求了,接着下来采用曲线的方法来构造数据集,然后让系统自动地计算两个数所集的交集。
先来看一个简单的例子,把正弦曲线与X轴围成的区域进行填充,如下图所示:
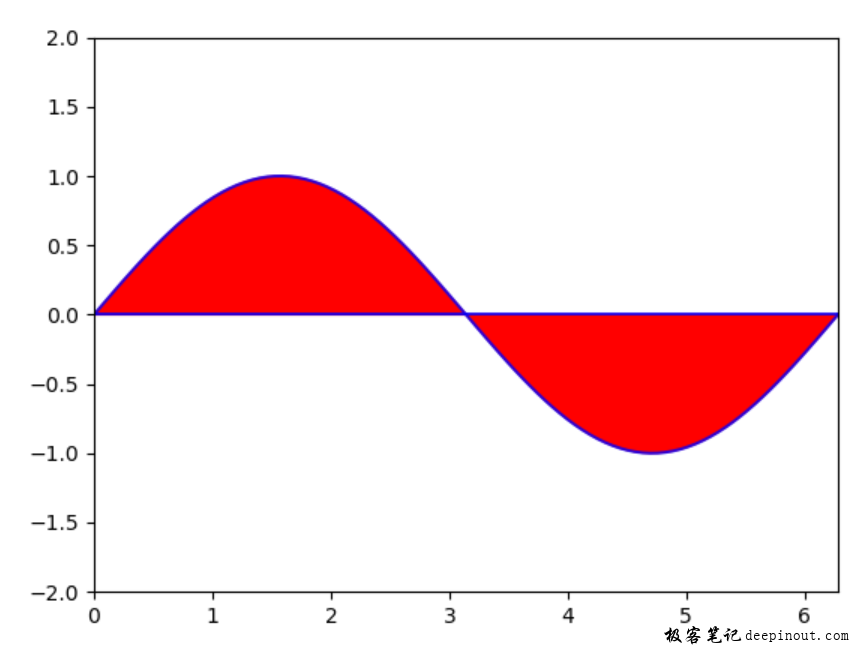
往往不规则的图形填充,都是由曲线生成,或者曲线相交生成。这里是采用正弦曲线与X轴围成,因此在代码计算0到2*np.pi的值,就是正弦曲线的一个周期。下面的代码:
x = np.linspace(0, 2*np.pi, 100)
就是实现了0到2*np.pi分成100个点,然后把这100个点当作X轴的坐标,接着调用函数np.sin(x)来计算100个点对应的正弦值,再把x和 y 放到填充函数里进行填充,如下:
host.fill(x, y, color = 'r')
这时就可以把不规则的区域填充为红色,因为color参数设置为r,就是表示红色。如果你想设置为别的颜色,就可以修改这个参数。
接着下来,就是使用函数对整个图形的轮廓进行画线,如下:
host.plot(x, y, color = 'b', alpha = 0.8)
host.plot([x[0], x[-1]], [y[0], y[-1]], color = 'b', alpha = 0.8)
这里调用的函数host.plot()在前面已经学习过了,比较熟悉,如果还不会请看前面的文章。这里color参数同样是设置线的颜色,alpha是设置透明度,也就是混合线的颜色和背景的颜色,如果设置为1,就完全不透明;如果设置为0,就是完全透明。
整个例子的代码如下:
import numpy as np
import matplotlib.pyplot as plt
#
fig, host = plt.subplots() #创建子图
host.grid(False)
host.set_xlim(0, 2*np.pi)
host.set_ylim(-2, 2)
#填充正弦曲线
x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)
host.fill(x, y, color = 'r')
host.plot(x, y, color = 'b', alpha = 0.8)
host.plot([x[0], x[-1]], [y[0], y[-1]], color = 'b', alpha = 0.8)
plt.show()
接着下来再看一个相交的例子,如下图:
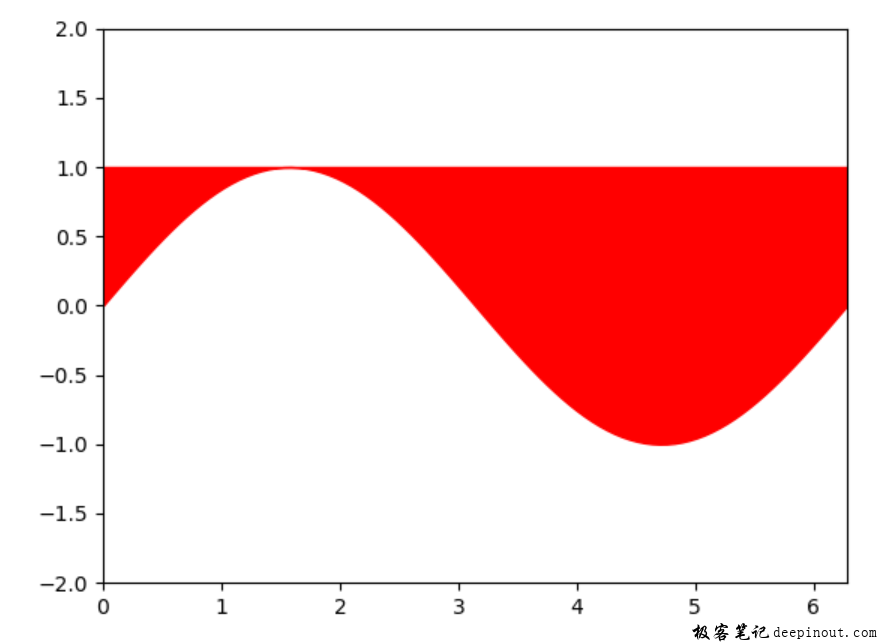
在这个例子里,主要填充正弦曲线与y = 1曲线之间的围成的区域,当然四边个坐标轴当作最大的填充线,就构造了这个图形。这里不是采用host.fill()函数,而是采用函数host.fill_between(),这个函数定义如下:
matplotlib.pyplot.fill_between(x, y1, y2=0, where=None, interpolate=False, step=None, *, data=None, **kwargs)
此函数用来填充两条水平曲线之间的区域,区域在点(x, y1) 和 (x, y2)之间,如果还想有条件地选择区域,可以采用where参数。
这个例子的代码如下:
import numpy as np
import matplotlib.pyplot as plt
#
fig, host = plt.subplots() #创建子图
host.grid(False)
host.set_xlim(0, 2*np.pi)
host.set_ylim(-2, 2)
#填充正弦曲线
x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)
host.fill_between(x,y, 1, color = 'r')
plt.show()
 极客笔记
极客笔记