前面实现两条曲线围成的区域进行指定的颜色填充,可以解决大部分问题了,但是有时候需要指定两条曲线在交叉点作为分界点,比如X轴小于交叉点的使用一种颜色来填充,X轴大于交叉点的区域,又采用另外一种颜色来填充。因为这种情况常常反映了某种条件进行了突变,进行量上的变化,从而达到质的变化。在做实验报告,或者PPT数据显示时,常常要标注出这种变化的关系,否则作为研究报告是不合格的,作为教学课件更加不合格了。
下面来看一个例子,如下图:
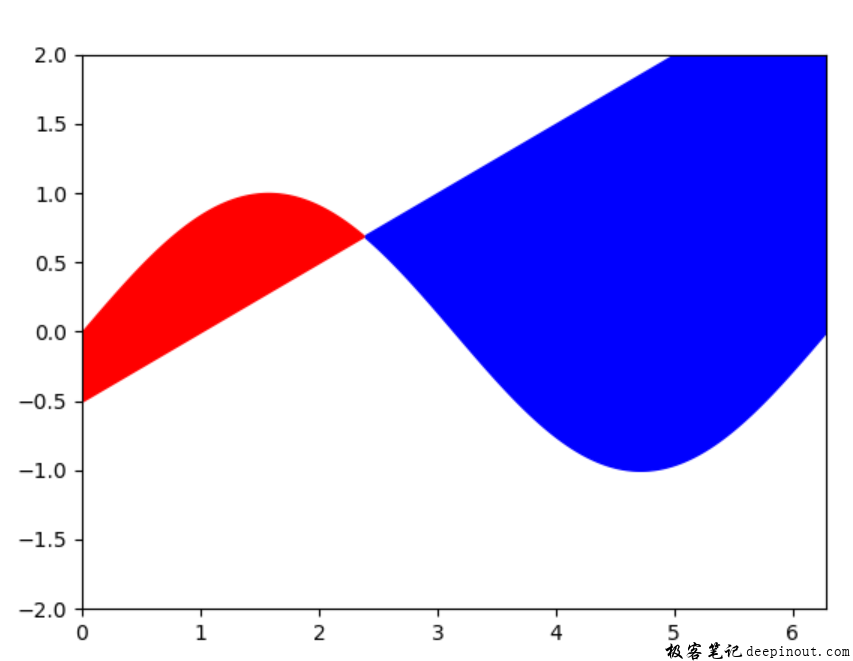
在这个图里,先看到两个区域填充了两种不同的颜色,在左边的区域填充是红色,在右边的区域填充是蓝色,并且这两个区域是不规则的形状,由此可见,它们是由两条曲线相交围成的区域图。一条曲线是正弦曲线,另外一条曲线是y1 = 0.5*x - 0.5的直线。正弦曲线与直线相交一点,这个交点是表示直线值y1比正弦值y小,相反另外一段是表示直线值y1比正弦值y大。要想在代码里实现这个条件判断,需要where条件,虽然在前面的文章到这个条件,但是没有实际的例子,感觉到还是不会使用。下面来看这行代码:
host.fill_between(x,y, y1, where = y1 <= y, color = 'r')
这里where = y1 <= y就是添加了判断条件,如果想要更复杂的条件就需要自己写上去。
其它的代码跟前面的例子是一样的,完整的代码如下:
import numpy as np
import matplotlib.pyplot as plt
#
fig, host = plt.subplots() #创建子图
host.grid(False)
host.set_xlim(0, 2*np.pi)
host.set_ylim(-2, 2)
#正弦曲线
x = np.linspace(0, 2*np.pi, 500)
y = np.sin(x)
#直线
y1 = 0.5*x - 0.5
host.fill_between(x,y, y1, where = y1 <= y, color = 'r')
host.fill_between(x,y, y1, where = y1 > y, color = 'b')
plt.show()
下面再来举一个常常用到的例子,就是显示置信区间。置信区间是指由样本统计量所构造的总体参数的估计区间。在统计学中,一个概率样本的置信区间(Confidence interval)是对这个样本的某个总体参数的区间估计。置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度,其给出的是被测量参数的测量值的可信程度,即前面所要求的“一个概率”。
如果只是使用文字来理解这个概念要比较困难的,那么采用图的方式又会怎么样?如下图:
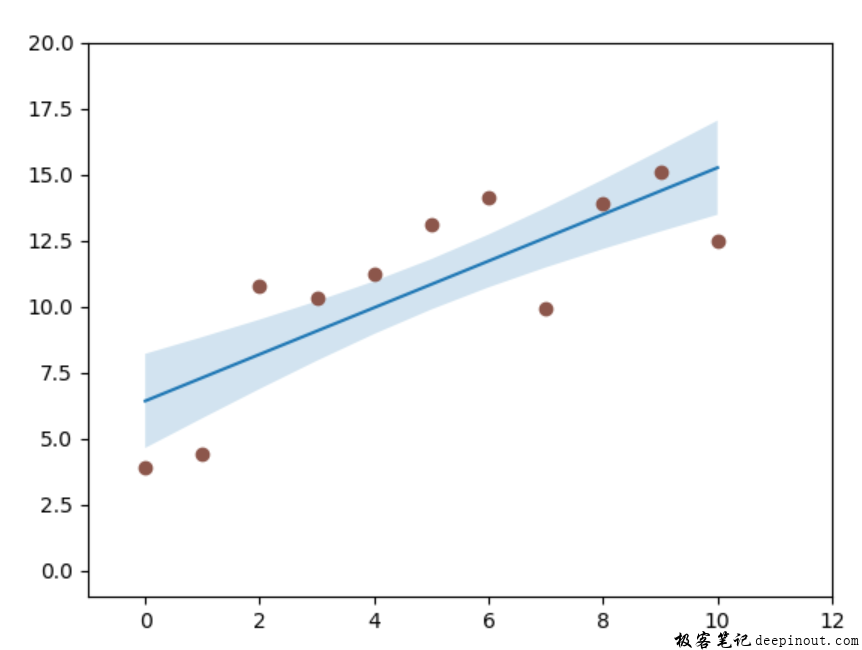
在上图里,采集到11个样本数据,然后进行直线拟合,根据数据的标准差进行置信区间计算,然后显示为半透明的区域。可以明显地看到置信区间在这个数据区域,比直接看一个置信区间值容易得多了,这个就是图像的威力。
如果你需要计算置信区间,也可以参考这种方式来显示,肯定会让更多人明白你的数据。这个例子的完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
#
fig, host = plt.subplots() #创建子图
host.grid(False)
host.set_xlim(-1, 12)
host.set_ylim(-1, 20)
#
x = np.linspace(0, 10, 11)
y = [3.9, 4.4, 10.8, 10.3, 11.2, 13.1, 14.1, 9.9, 13.9, 15.1, 12.5]
# 拟合一条直线,估计y值,并计算误差。
a, b = np.polyfit(x, y, deg=1)
y_est = a * x + b
y_err = x.std() * np.sqrt(1/len(x) +
(x - x.mean())**2 / np.sum((x - x.mean())**2))
host.plot(x, y_est, '-') #连接拟合直线
host.fill_between(x, y_est - y_err, y_est + y_err, alpha=0.2) #置信区间填充
host.plot(x, y, 'o', color='tab:brown') #标记数据点位置
plt.show()
通过图示的方式,肯定比看到95%的数字更加直观,更加形象。
 极客笔记
极客笔记