Java 包含元音字母的最长公共子序列长度
在这个问题中,我们的任务是找到两个字符串中可能存在的最长子序列的长度,其中子序列的每个字母必须是一个元音字母。通过递归算法和迭代算法,可以解决给定的问题陈述。在英文字母表中,存在五个元音字母,分别命名为’A’、’E’、’I’、’O’、’U’。子序列与子字符串的区别:在子序列中,我们可以以非连续的方式取字符,但在子字符串中,我们只能取连续的字符。
例如,在字符串“TutorialsPoint”中,“tri”是一个子序列,但不是一个子字符串。而“tor”既是子序列又是子字符串。
示例
示例1
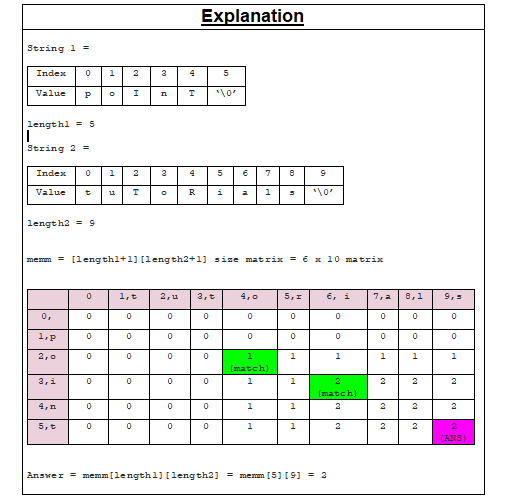
字符串1:“point”
字符串2:“tutorials”
包含元音字母的共同子序列的长度:2
示例2
字符串1:“longestsub”
字符串2:“ohbekhfuo”
包含元音字母的共同子序列的长度:3
递归子结构
If idx_1 = 0 or idx_2 = 0, Then
LCSVowels(idx1, idx2) = 0
Else If str1[idx_1-1] = str2[idx_2-1] and str1[idx_1-1] = Vowel, Then
LCSVowels(idx_1, idx_2) = 1 + LCSVowels(idx_1-1, idx_2-1)
Else
LCSVowels(idx_1, idx_2) = max(LCSVowels(idx_1, idx_2-1), LCSVowels(idx_1-1, idx_2))
多种方法
我们提供了不同的解决方案。
- 迭代算法。
-
递归算法。
方法1:迭代算法
这是基于迭代算法的动态规划方法。
算法:LCSVowels(string1, string2)
步骤-1: length1 = LENGTH(string1)
步骤-2: length2 = LENGTH(string2)
步骤-3: 创建大小为(length1+1)X(length2+1)的二维整数数组“memm”。
步骤-4: 将第一行的所有列都设置为0。
步骤-5: 将第一列的所有行都设置为0。
步骤-6: 使用for循环LOOP(idx_1 = 1到length1)
步骤-7: 使用内部循环LOOP(idx_2 = 1到length2)
步骤-8: 检查条件IF(string1[idx_1-1] string2[idx_2-1] AND string1[idx_1-1] VOWEL),然后
步骤-9: memm[idx_1][idx_2] = 1 + memm[idx_1-1][idx_2-1];
步骤-10: 否则,memm[idx_1][idx_2]=MAX(memm[idx_1][idx_2-1],memm[idx_1-1][idx_2])
步骤-11:返回memm[length1][length2]
代码
#include <iostream>
using namespace std;
/**
* @param ch: character parameter
*
* @return true: if ch == vowel
* @return false: if ch == consonent
*/
bool checkVowel(char chr) {
switch(chr) {
case 'A':
case 'E':
case 'I':
case 'O':
case 'U':
case 'a':
case 'e':
case 'i':
case 'o':
case 'u':
return true;
break;
default:
return false;
break;
}
}
/**
* @param num1: first number
* @param num2: second number
*
* @return maximum number
*/
int maxx(int first, int second) {
if (first >= second)
return first;
else
return second;
}
/**
* @param string1: First String
* @param string2: Second String
*
* @return Length of maximum common subsequence containing vowels
*/
int LCSVowels(string string1, string string2) {
int length1 = string1.length();
int length2 = string2.length();
// create memory array for using Dynamic Programming
int memm[length1+1][length2+2];
// make first column zero
for (int idx_ = 0; idx_ <= length1; ++idx_) {
memm[idx_][0] = 0;
}
// make first row zero
for (int idx_=0; idx_ <= length2; ++idx_) {
memm[0][idx_] = 0;
}
// traverse the DP matrix
for (int idx_1=1; idx_1<=length1; ++idx_1) {
for (int idx_2=1; idx_2<=length2; ++idx_2) {
// if characters are equal and also they are vowels
if (string1[idx_1-1] == string2[idx_2-1] && checkVowel(string1[idx_1-1])) {
memm[idx_1][idx_2] = 1 + memm[idx_1-1][idx_2-1];
} else {
memm[idx_1][idx_2] = maxx(memm[idx_1][idx_2-1], memm[idx_1-1][idx_2]);
}
}
}
return memm[length1][length2];
}
int main() {
string string1, string2;
// Ask string 1
cout << "Enter String 1: ";
cin >> string1;
// Ask String 2
cout << "Enter String 2: ";
cin >> string2;
// call the function
int lcs = LCSVowels(string1, string2);
// display the result
cout << "Length of Longest Common Subsequence containing vowels: " << lcs << endl;
return 0;
}
输出
Enter String 1: point
Enter String 2: tutorials
Length of Longest Common Subsequence containing vowels: 2
程序的时间复杂度 = O(length1 x length2)
程序的空间复杂度 = O(length1 x length2)
方法2:递归算法
这是基于递归算法的动态规划方法。
算法:LCS_Vowels(string1, string2, idx1, idx2, memm)
步骤1 :如果(idx1 -1或者idx2 -1),那么返回0
步骤2 :如果(memm[idx1][idx2] != -1),那么返回memm[idx1][idx2]
步骤3 :如果(string1[idx_1] string2[idx_2]并且string1[idx_1]是元音),那么
步骤4 :memm[idx1][idx2] = 1 + LCS_Vowels(string1, string2, idx1-1, idx2-1, memm)
步骤5 :否则,设置memm[idx1][idx2] = MAX(LCS_Vowels(string1, string2, idx1-1, idx2, memm) , LCS_Vowels(string1, string2, idx1, idx2-1, memm))
步骤7 :结束如果
步骤8 :返回memm[idx1][idx2]
示例
#include <iostream>
using namespace std;
/**
* @param ch: character parameter
*
* @return true: if ch == vowel
* @return false: if ch == consonent
*/
bool check_Vowel(char _chr) {
switch(_chr) {
case 'A':
case 'E':
case 'I':
case 'O':
case 'U':
case 'a':
case 'e':
case 'i':
case 'o':
case 'u':
return true;
break;
default:
return false;
break;
}
}
/**
* @param num1: first number
* @param num2: second number
*
* @return maximum number
*/
int maxx(int first, int second) {
if (first >= second)
return first;
else
return second;
}
/**
* @param ABC: First String
* @param XYZ: Second String
* @param ABC_IDX: index for string-A
* @param XYZ_IDX: index for string-B
* @param memm: DP matrix
*/
int LCS_Vowels(string ABC, string XYZ, int ABC_IDX, int XYZ_IDX, int memm[1000][1000]) {
if (ABC_IDX == -1 || XYZ_IDX == -1)
return 0;
if (memm[ABC_IDX][XYZ_IDX] != -1)
return memm[ABC_IDX][XYZ_IDX];
if (ABC[ABC_IDX] == XYZ[XYZ_IDX] && check_Vowel(ABC[ABC_IDX])) {
memm[ABC_IDX][XYZ_IDX] = LCS_Vowels(ABC, XYZ, ABC_IDX-1, XYZ_IDX-1, memm) + 1;
} else {
memm[ABC_IDX][XYZ_IDX] = maxx(
LCS_Vowels(ABC, XYZ, ABC_IDX-1, XYZ_IDX, memm),
LCS_Vowels(ABC, XYZ, ABC_IDX, XYZ_IDX-1, memm)
);
}
return memm[ABC_IDX][XYZ_IDX];
}
int main() {
string ABC, XYZ;
// Ask string 1
cout << "Enter String 1: ";
cin >> ABC;
// Ask String 2
cout << "Enter String 2: ";
cin >> XYZ;
int LENGTH_1 = ABC.length();
int LENGTH_2 = XYZ.length();
int memm[1000][1000];
for (int p=0; p<1000; ++p) {
for (int q=0; q<1000; ++q) {
memm[p][q] = -1;
}
}
// call the function
int lcs = LCS_Vowels(ABC, XYZ, LENGTH_1-1, LENGTH_2-1, memm);
// display the result
cout << "Length of Longest Common Subsequence containing vowels: " << lcs << endl;
return 0;
}
输出
Enter String 1: longestsub
Enter String 2: ohbekhfuo
Length of Longest Common Subsequence containing vowels: 3
程序的时间复杂度 = O(长度1 x 长度2)
程序的空间复杂度 = O(长度1 x 长度2)
最后,本文成功地使用动态规划解决了给定问题的C++代码。该算法使用了O(长度1 x 长度2)的时间复杂度和空间复杂度来解决问题。
 极客笔记
极客笔记