从连通图中删除一个顶点以获得一个连通子图

问题描述

我有这样的印象，如果我取一个简单的连通图，那么我可以（假设它具有顶点数量大于等于2）删除一个顶点并获得一个连通子图。

但并非所有顶点都适用，有些顶点我不能删除。 例如，

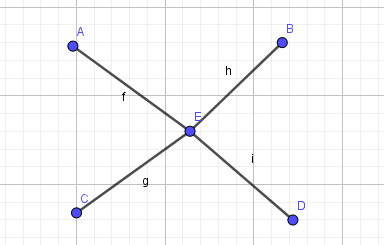
我不能删除E，否则就会丢失连通性，但我可以删除A、B、C或D。

但总有一个我可以排除。你有办法证明这个结果吗？

解决方案

设G为任意连通图。那么G至少有一棵生成树。设T为G的任意生成树。设v为T的任意叶子节点。如果我们删除v，T \ {v}是连通的，并且是G \ {v}的子图，因此G \ {v}是连通的。

这个方案使用了以下已知结果：

• 每个连通图至少有1棵生成树
• 从一棵有n个顶点的树中删除一个叶子节点将得到一棵有(n-1)个顶点的树