如何使用 Pandas 计算相关系数|极客笔记

如何使用 Pandas 计算相关系数

在数据分析中，相关系数是一种用于量化两个变量之间线性关系强度的统计指标。Pandas 是 Python 数据分析库，提供了计算相关系数的功能，非常适合处理和分析大型数据集。本文将详细介绍如何使用 Pandas 计算相关系数，包括不同类型的相关系数计算方法以及相关的应用场景。

1. 理解相关系数

相关系数的值范围从 -1 到 1。值为 1 表示完全正相关，值为 -1 表示完全负相关，值为 0 表示没有线性关系。Pandas 主要支持以下几种类型的相关系数：

Pearson 相关系数
Spearman 秩相关系数
Kendall’s Tau 相关系数

示例代码 1：创建 DataFrame

import pandas as pd
import numpy as np

# 创建一个 DataFrame
data = {
    'A': np.random.randn(100),
    'B': np.random.rand(100)
}
df = pd.DataFrame(data)
print(df.head())

Output:

如何使用 Pandas 计算相关系数

示例代码 2：计算 Pearson 相关系数

import pandas as pd
import numpy as np

data = {
    'A': np.random.randn(100),
    'B': np.random.rand(100)
}
df = pd.DataFrame(data)

# 计算 Pearson 相关系数
pearson_corr = df.corr(method='pearson')
print(pearson_corr)

Output:

如何使用 Pandas 计算相关系数

示例代码 3：计算 Spearman 秩相关系数

import pandas as pd
import numpy as np

data = {
    'A': np.random.randn(100),
    'B': np.random.rand(100)
}
df = pd.DataFrame(data)

# 计算 Spearman 秩相关系数
spearman_corr = df.corr(method='spearman')
print(spearman_corr)

Output:

如何使用 Pandas 计算相关系数

示例代码 4：计算 Kendall’s Tau 相关系数

import pandas as pd
import numpy as np

data = {
    'A': np.random.randn(100),
    'B': np.random.rand(100)
}
df = pd.DataFrame(data)

# 计算 Kendall's Tau 相关系数
kendall_corr = df.corr(method='kendall')
print(kendall_corr)

Output:

如何使用 Pandas 计算相关系数

2. 应用相关系数

相关系数在许多领域都有广泛的应用，例如在金融分析、生物统计、社会科学等领域。通过分析变量之间的相关性，可以帮助我们理解数据特征之间的关系，进行更有效的数据分析和预测。

示例代码 5：分析股票数据的相关性

import pandas as pd
import numpy as np

# 假设有两只股票的收盘价数据
data = {
    'Stock_A': np.random.randn(100) * 100 + 1000,
    'Stock_B': np.random.randn(100) * 50 + 500
}
df = pd.DataFrame(data)

# 计算两只股票收盘价的 Pearson 相关系数
stock_corr = df.corr(method='pearson')
print(stock_corr)

Output:

如何使用 Pandas 计算相关系数

示例代码 6：使用相关系数进行特征选择

import pandas as pd
import numpy as np

# 假设有一个包含多个特征的数据集
data = {
    'Feature_1': np.random.randn(100),
    'Feature_2': np.random.rand(100),
    'Target': np.random.randint(0, 2, 100)
}
df = pd.DataFrame(data)

# 计算特征与目标变量之间的相关系数
feature_corr = df.corr(method='pearson')
print(feature_corr)

Output:

如何使用 Pandas 计算相关系数

示例代码 7：探索数据集中的多变量相关性

import pandas as pd
import numpy as np

data = {
    'Feature_1': np.random.randn(100),
    'Feature_2': np.random.rand(100),
    'Feature_3': np.random.randint(0, 100, 100)
}
df = pd.DataFrame(data)

# 计算所有变量之间的相关系数矩阵
multi_corr = df.corr(method='pearson')
print(multi_corr)

Output:

如何使用 Pandas 计算相关系数

3. 可视化相关系数

可视化是理解相关系数的一个重要工具。通过可视化，我们可以更直观地看到不同变量之间的相关性强度和方向。

示例代码 8：使用热图可视化相关系数矩阵

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

data = {
    'Feature_1': np.random.randn(100),
    'Feature_2': np.random.rand(100),
    'Feature_3': np.random.randint(0, 100, 100)
}
df = pd.DataFrame(data)

# 计算相关系数矩阵
corr_matrix = df.corr(method='pearson')

# 使用 seaborn 绘制热图
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm')
plt.show()

Output:

如何使用 Pandas 计算相关系数

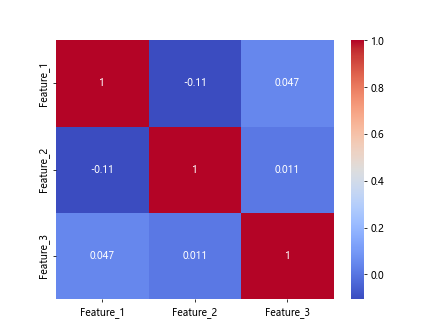
示例代码 9：散点图矩阵

import pandas as pd
import numpy as np
import seaborn as sns

data = {
    'Feature_1': np.random.randn(100),
    'Feature_2': np.random.rand(100),
    'Feature_3': np.random.randint(0, 100, 100)
}
df = pd.DataFrame(data)

# 使用 seaborn 绘制散点图矩阵
sns.pairplot(df)
plt.show()

4. 处理相关系数的注意事项

在使用相关系数时，需要注意一些问题，例如数据的分布、异常值的影响以及变量之间的非线性关系等。

示例代码 10：处理异常值

import pandas as pd
import numpy as np

data = {
    'Feature_1': np.append(np.random.randn(99), 10),  # 添加一个异常值
    'Feature_2': np.random.rand(100)
}
df = pd.DataFrame(data)

# 计算相关系数前处理异常值
df['Feature_1'] = np.where(df['Feature_1'] > 3, np.median(df['Feature_1']), df['Feature_1'])

# 计算相关系数
cleaned_corr = df.corr(method='pearson')
print(cleaned_corr)

Output:

如何使用 Pandas 计算相关系数