当前位置：极客笔记 > Matplotlib > Matplotlib 问答 > 使用Python和Matplotlib绘制参数方程定义的3D曲面

使用Python和Matplotlib绘制参数方程定义的3D曲面

使用Python和Matplotlib绘制参数方程定义的3D曲面

参考：Rendering 3D Surfaces Using Parametric Equations in Python

在科学可视化和数据分析领域，三维曲面的渲染是一个常见且重要的任务。Python作为一种强大的编程语言，结合Matplotlib库，为我们提供了一套灵活而强大的工具来创建和可视化复杂的3D曲面。本文将深入探讨如何使用参数方程在Python中渲染3D曲面，涵盖从基础概念到高级技巧的全面内容。

1. 参数方程与3D曲面的基本概念

在开始实际编码之前，我们需要理解参数方程和3D曲面的基本概念。参数方程是用一组参数来表示曲线或曲面上点的坐标的方程。对于3D曲面，我们通常使用两个参数（例如u和v）来定义空间中的点（x, y, z）。

一般形式如下：
x = f(u, v)
y = g(u, v)
z = h(u, v)

其中u和v是参数，f、g和h是定义曲面形状的函数。

让我们看一个简单的例子，使用参数方程绘制一个球体：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建参数网格
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)
u, v = np.meshgrid(u, v)

# 定义球体的参数方程
r = 2  # 球体半径
x = r * np.sin(v) * np.cos(u)
y = r * np.sin(v) * np.sin(u)
z = r * np.cos(v)

# 创建3D图形
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制曲面
surf = ax.plot_surface(x, y, z, cmap='viridis')

# 设置标题和标签
ax.set_title('Sphere - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

# 添加颜色条
fig.colorbar(surf)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

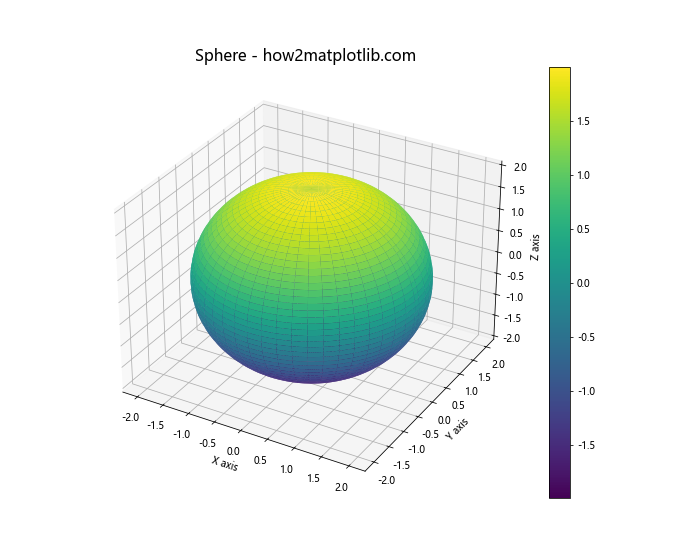
在这个例子中，我们使用了球坐标系的参数方程来定义一个半径为2的球体。np.meshgrid函数用于创建参数网格，这是绘制3D曲面的关键步骤。

2. Matplotlib中的3D绘图基础

Matplotlib是Python中最流行的绘图库之一，它提供了强大的3D绘图功能。要使用Matplotlib绘制3D图形，我们需要导入mpl_toolkits.mplot3d模块。

以下是一个基本的3D图形设置示例：

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 这里添加绘图代码

ax.set_title('3D Surface - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

这段代码创建了一个基本的3D图形环境。fig.add_subplot(111, projection='3d')创建了一个3D坐标系，我们可以在这个坐标系中添加各种3D图形元素。

3. 使用参数方程绘制简单的3D曲面

让我们从一个简单的例子开始，绘制一个抛物面：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建参数网格
u = np.linspace(-2, 2, 100)
v = np.linspace(-2, 2, 100)
u, v = np.meshgrid(u, v)

# 定义抛物面的参数方程
x = u
y = v
z = u**2 + v**2

# 创建3D图形
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制曲面
surf = ax.plot_surface(x, y, z, cmap='coolwarm')

# 设置标题和标签
ax.set_title('Paraboloid - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

# 添加颜色条
fig.colorbar(surf)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

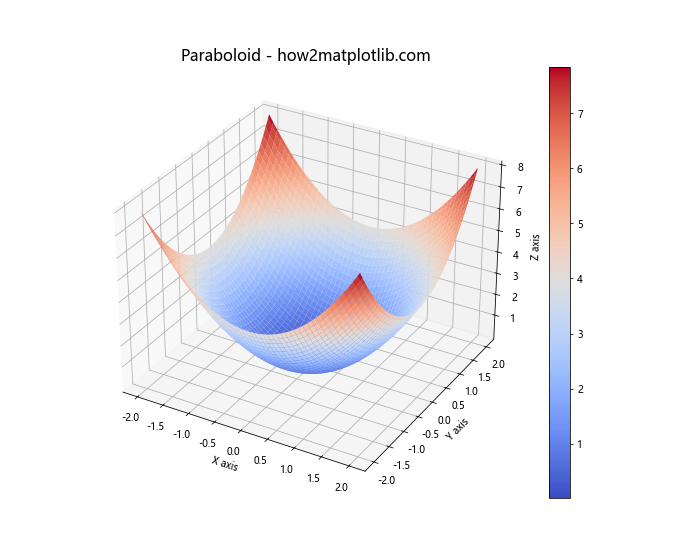
在这个例子中，我们定义了一个简单的抛物面z = x^2 + y^2。plot_surface函数用于绘制3D曲面，cmap参数指定了颜色映射。

4. 复杂曲面的参数方程

现在让我们尝试一些更复杂的曲面。以下是一个螺旋面的例子：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建参数网格
u = np.linspace(0, 4*np.pi, 100)
v = np.linspace(-2, 2, 100)
u, v = np.meshgrid(u, v)

# 定义螺旋面的参数方程
r = 1 + v/4
x = r * np.cos(u)
y = r * np.sin(u)
z = v

# 创建3D图形
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制曲面
surf = ax.plot_surface(x, y, z, cmap='plasma')

# 设置标题和标签
ax.set_title('Helicoid - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

# 添加颜色条
fig.colorbar(surf)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

这个例子展示了如何使用参数方程创建一个螺旋面。通过调整参数方程，我们可以创造出各种有趣的形状。

5. 自定义曲面外观

Matplotlib提供了多种方法来自定义3D曲面的外观。以下是一些常用的技巧：

5.1 更改颜色映射

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建参数网格
u = np.linspace(-2, 2, 100)
v = np.linspace(-2, 2, 100)
u, v = np.meshgrid(u, v)

# 定义曲面方程
x = u
y = v
z = np.sin(np.sqrt(u**2 + v**2))

# 创建3D图形
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制曲面，使用自定义颜色映射
surf = ax.plot_surface(x, y, z, cmap='viridis', alpha=0.8)

# 设置标题和标签
ax.set_title('Custom Colormap - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

# 添加颜色条
fig.colorbar(surf)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

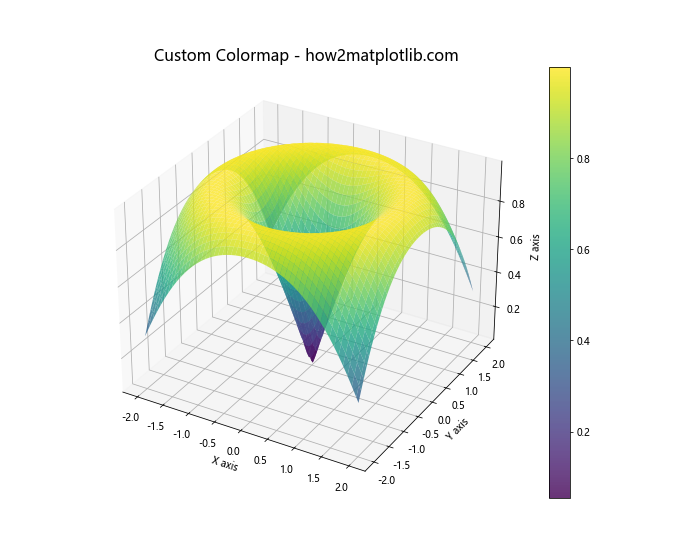
在这个例子中，我们使用了’viridis’颜色映射，并设置了透明度（alpha）为0.8。

5.2 调整视角

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建参数网格
u = np.linspace(-2, 2, 100)
v = np.linspace(-2, 2, 100)
u, v = np.meshgrid(u, v)

# 定义曲面方程
x = u
y = v
z = np.sin(u) * np.cos(v)

# 创建3D图形
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制曲面
surf = ax.plot_surface(x, y, z, cmap='coolwarm')

# 设置视角
ax.view_init(elev=20, azim=45)

# 设置标题和标签
ax.set_title('Adjusted View - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

# 添加颜色条
fig.colorbar(surf)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

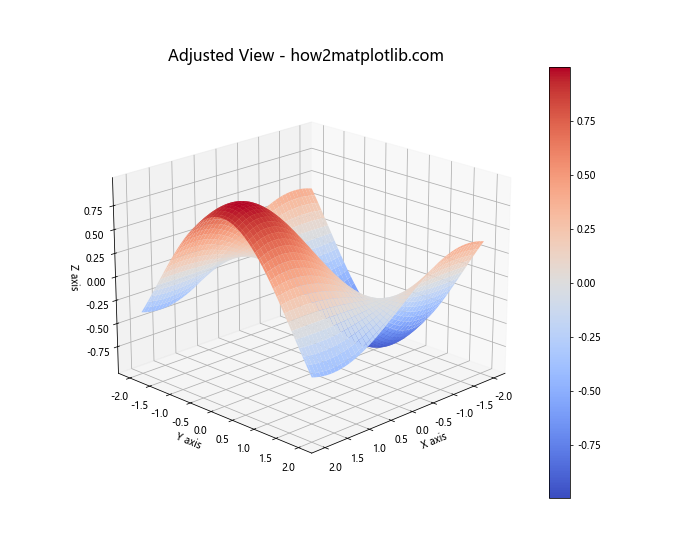
view_init函数用于调整视角，elev参数控制仰角，azim参数控制方位角。

6. 添加等高线

在3D曲面上添加等高线可以帮助更好地理解曲面的形状：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建参数网格
u = np.linspace(-3, 3, 100)
v = np.linspace(-3, 3, 100)
u, v = np.meshgrid(u, v)

# 定义曲面方程
x = u
y = v
z = np.sin(np.sqrt(u**2 + v**2))

# 创建3D图形
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制曲面
surf = ax.plot_surface(x, y, z, cmap='viridis', alpha=0.8)

# 添加等高线
contours = ax.contour(x, y, z, zdir='z', offset=-2, cmap='coolwarm')

# 设置标题和标签
ax.set_title('Surface with Contours - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

# 设置z轴范围
ax.set_zlim(-2, 1)

# 添加颜色条
fig.colorbar(surf)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

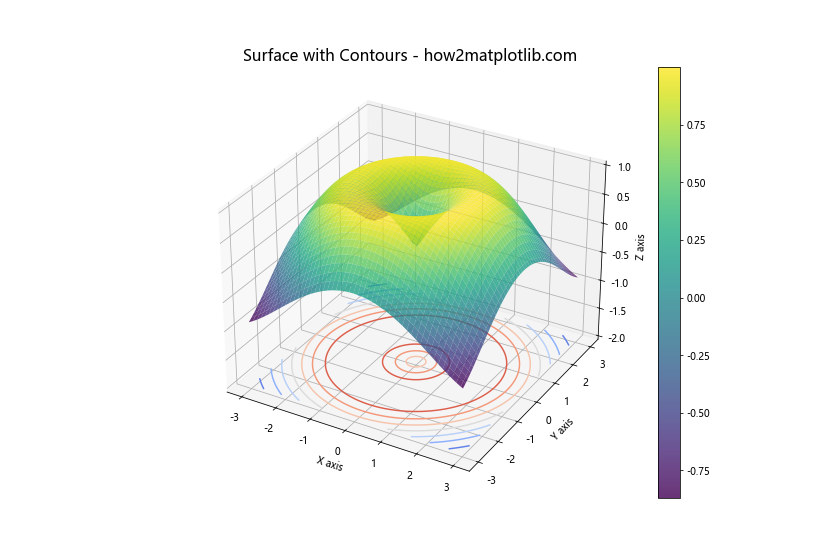
在这个例子中，我们使用contour函数在z=-2的平面上添加了等高线。

7. 组合多个曲面

有时我们需要在同一个图中绘制多个3D曲面。以下是一个例子：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建参数网格
u = np.linspace(-2, 2, 50)
v = np.linspace(-2, 2, 50)
u, v = np.meshgrid(u, v)

# 定义两个曲面
z1 = np.sin(np.sqrt(u**2 + v**2))
z2 = np.cos(np.sqrt(u**2 + v**2))

# 创建3D图形
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制两个曲面
surf1 = ax.plot_surface(u, v, z1, cmap='viridis', alpha=0.7)
surf2 = ax.plot_surface(u, v, z2, cmap='plasma', alpha=0.7)

# 设置标题和标签
ax.set_title('Multiple Surfaces - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

# 添加颜色条
fig.colorbar(surf1, shrink=0.5, aspect=5)
fig.colorbar(surf2, shrink=0.5, aspect=5)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

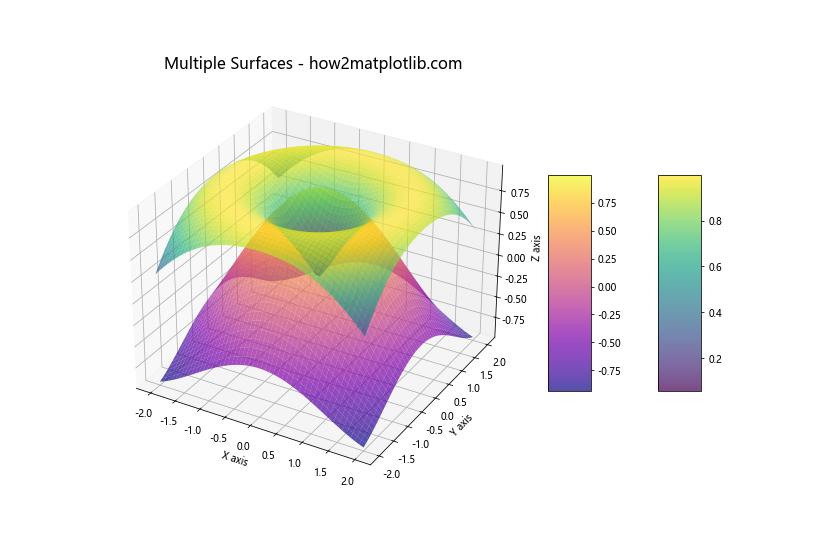
这个例子展示了如何在同一个图中绘制两个不同的3D曲面，并为每个曲面添加单独的颜色条。

8. 动画效果

我们还可以创建3D曲面的动画效果。以下是一个简单的例子：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.animation import FuncAnimation

# 创建参数网格
u = np.linspace(-2, 2, 50)
v = np.linspace(-2, 2, 50)
u, v = np.meshgrid(u, v)

# 创建3D图形
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 初始化曲面
surf = ax.plot_surface(u, v, np.zeros_like(u), cmap='viridis')

# 更新函数
def update(frame):
    z = np.sin(np.sqrt(u**2 + v**2) - frame)
    ax.clear()
    surf = ax.plot_surface(u, v, z, cmap='viridis')
    ax.set_title(f'Animated Surface - Frame {frame} - how2matplotlib.com', fontsize=16)
    ax.set_zlim(-1, 1)
    return surf,

# 创建动画
anim = FuncAnimation(fig, update, frames=np.linspace(0, 2*np.pi, 100),
                     interval=50, blit=False)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

这个例子创建了一个简单的波动曲面动画。FuncAnimation函数用于生成动画，update函数定义了每一帧的更新逻辑。

9. 高级技巧：自定义着色

我们可以使用自定义的着色方法来增强3D曲面的视觉效果。以下是一个使用自定义着色的例子：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import LightSource

# 创建参数网格
u = np.linspace(-3, 3, 100)
v = np.linspace(-3, 3, 100)
u, v = np.meshgrid(u, v)

# 定义曲面方程
x = u
y = v
z = np.sin(np.sqrt(u**2 + v**2))

# 创建3D图形
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 创建光源对象
ls = LightSource(azdeg=315, altdeg=45)

# 使用光源对象创建着色
rgb = ls.shade(z, plt.cm.copper)

# 绘制曲面
surf = ax.plot_surface(x, y, z, rstride=1, cstride=1, facecolors=rgb,
                       linewidth=0, antialiased=False, shade=False)

# 设置标题和标签
ax.set_title('Custom Shading - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

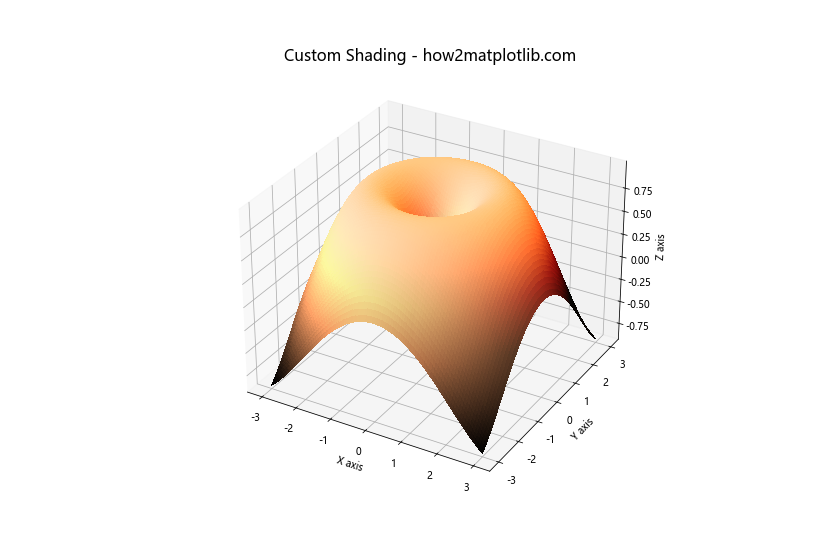
在这个例子中，我们使用LightSource对象来创建自定义的光照效果。这种技术可以增强3D曲面的立体感和细节。

10. 复杂参数方程：莫比乌斯带

莫比乌斯带是一个有趣的数学对象，我们可以用参数方程来绘制它：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建参数网格
u = np.linspace(0, 2*np.pi, 100)
v = np.linspace(-1, 1, 50)
u, v = np.meshgrid(u, v)

# 定义莫比乌斯带的参数方程
R = 2
x = (R + v*np.cos(u/2)) * np.cos(u)
y = (R + v*np.cos(u/2)) * np.sin(u)
z = v * np.sin(u/2)

# 创建3D图形
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制曲面
surf = ax.plot_surface(x, y, z, cmap='viridis', alpha=0.8)

# 设置标题和标签
ax.set_title('Möbius Strip - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

# 添加颜色条
fig.colorbar(surf)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

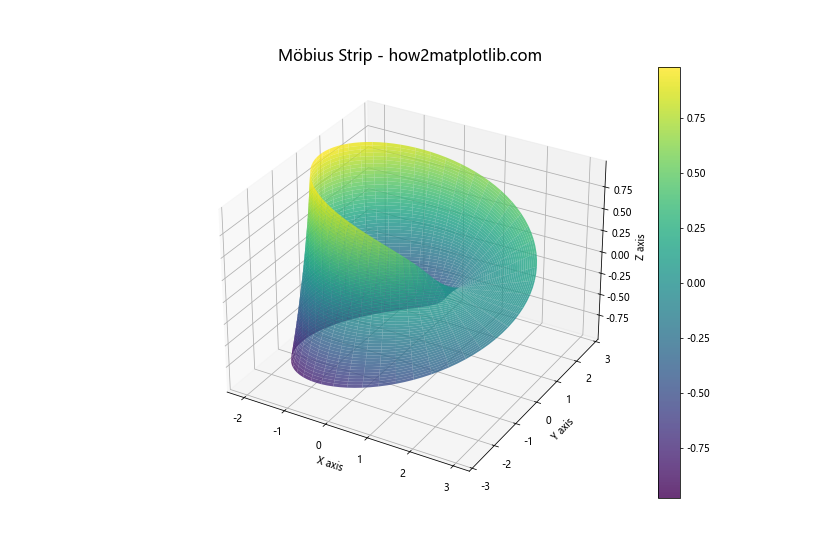
这个例子展示了如何使用参数方程绘制复杂的数学对象。莫比乌斯带是一个单面的曲面，这个特性在3D可视化中可以清楚地看到。

11. 使用极坐标系

有时，使用极坐标系来定义参数方程可能更方便。以下是一个使用极坐标系绘制花瓣形状的例子：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建参数网格
theta = np.linspace(0, 2*np.pi, 100)
phi = np.linspace(0, np.pi, 50)
theta, phi = np.meshgrid(theta, phi)

# 定义花瓣形状的参数方程
r = 2 + np.sin(3*theta)
x = r * np.sin(phi) * np.cos(theta)
y = r * np.sin(phi) * np.sin(theta)
z = r * np.cos(phi)

# 创建3D图形
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制曲面
surf = ax.plot_surface(x, y, z, cmap='coolwarm')

# 设置标题和标签
ax.set_title('Flower Shape in Polar Coordinates - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

# 添加颜色条
fig.colorbar(surf)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

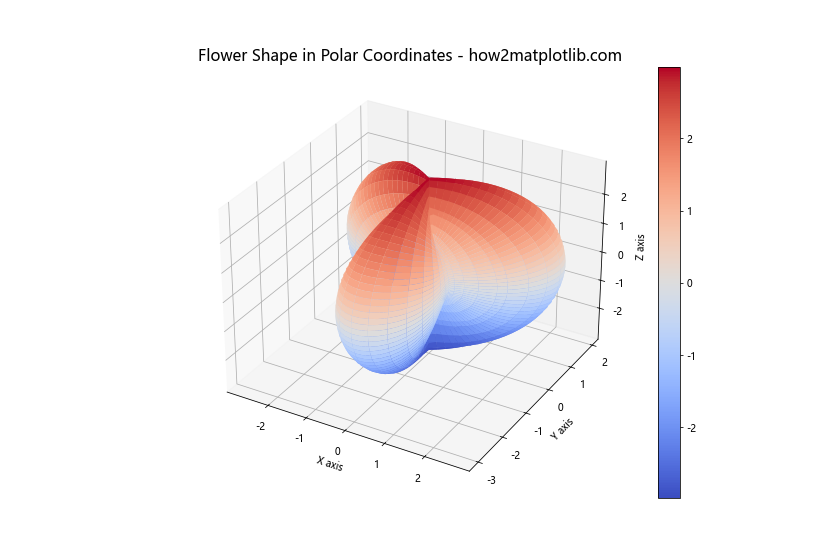
这个例子展示了如何使用极坐标系来创建复杂的3D形状。通过调整r的方程，我们可以创造出各种有趣的形状。

12. 添加交互性

Matplotlib还支持添加交互性到3D图形中。以下是一个简单的交互式3D曲面示例：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.widgets import Slider

# 创建参数网格
u = np.linspace(-2, 2, 100)
v = np.linspace(-2, 2, 100)
u, v = np.meshgrid(u, v)

# 创建3D图形
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')

# 初始参数
freq = 1

# 定义曲面函数
def surface(u, v, freq):
    return np.sin(freq * np.sqrt(u**2 + v**2))

# 初始化曲面
surf = ax.plot_surface(u, v, surface(u, v, freq), cmap='viridis')

# 设置标题和标签
ax.set_title('Interactive Surface - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

# 添加滑块
slider_ax = plt.axes([0.1, 0.02, 0.65, 0.03])
freq_slider = Slider(slider_ax, 'Frequency', 0.1, 5, valinit=freq)

# 更新函数
def update(val):
    ax.clear()
    freq = freq_slider.val
    surf = ax.plot_surface(u, v, surface(u, v, freq), cmap='viridis')
    ax.set_title('Interactive Surface - how2matplotlib.com', fontsize=16)
    ax.set_xlabel('X axis')
    ax.set_ylabel('Y axis')
    ax.set_zlabel('Z axis')
    fig.canvas.draw_idle()

freq_slider.on_changed(update)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

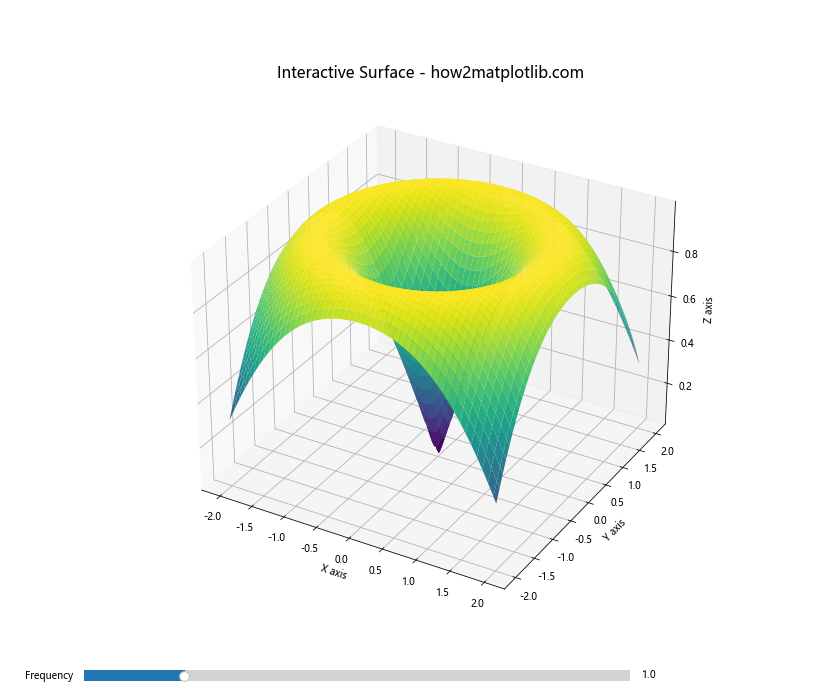
这个例子创建了一个带有滑块的交互式3D曲面。用户可以通过滑块来调整曲面的频率，实时看到曲面形状的变化。

13. 结合其他图形元素

我们可以将3D曲面与其他图形元素结合，以创建更丰富的可视化效果。以下是一个结合散点图的例子：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建参数网格
u = np.linspace(-2, 2, 50)
v = np.linspace(-2, 2, 50)
u, v = np.meshgrid(u, v)

# 定义曲面方程
z = np.sin(np.sqrt(u**2 + v**2))

# 创建3D图形
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制曲面
surf = ax.plot_surface(u, v, z, cmap='viridis', alpha=0.7)

# 生成随机点
n_points = 50
x_points = np.random.uniform(-2, 2, n_points)
y_points = np.random.uniform(-2, 2, n_points)
z_points = np.sin(np.sqrt(x_points**2 + y_points**2)) + np.random.normal(0, 0.1, n_points)

# 绘制散点
ax.scatter(x_points, y_points, z_points, c='red', s=50, alpha=1)

# 设置标题和标签
ax.set_title('Surface with Scattered Points - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

# 添加颜色条
fig.colorbar(surf)

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

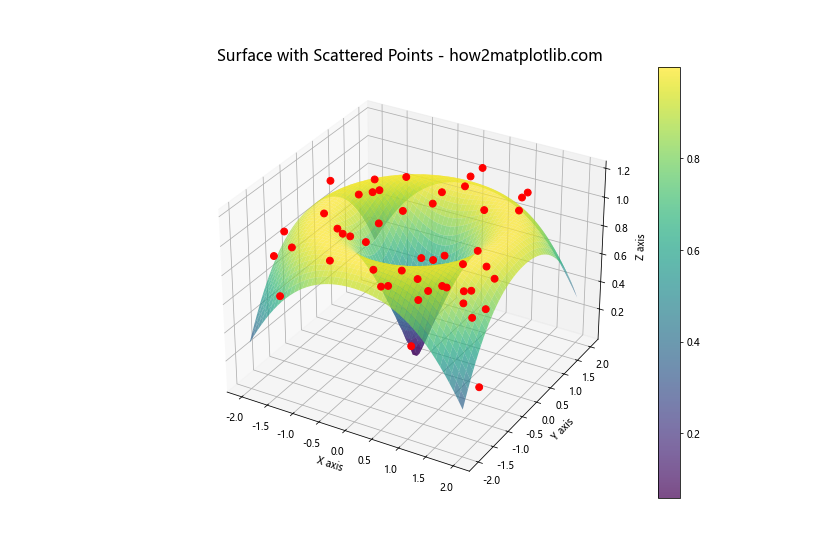
这个例子展示了如何在3D曲面上添加散点。这种技术可以用于显示数据点与理论模型的关系。

14. 优化性能

当处理大量数据点时，3D渲染可能会变得很慢。以下是一些优化性能的技巧：

  1. 减少数据点：使用更大的步长来创建网格。
  2. 使用线框图而不是实体曲面。
  3. 使用rstride和cstride参数来减少渲染的面数。

以下是一个使用这些技巧的例子：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建参数网格（使用更大的步长）
u = np.linspace(-2, 2, 50)
v = np.linspace(-2, 2, 50)
u, v = np.meshgrid(u, v)

# 定义曲面方程
z = np.sin(np.sqrt(u**2 + v**2))

# 创建3D图形
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制线框图
wire = ax.plot_wireframe(u, v, z, rstride=2, cstride=2, color='blue', alpha=0.5)

# 设置标题和标签
ax.set_title('Optimized Wireframe Plot - how2matplotlib.com', fontsize=16)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

plt.show()

Output:

使用Python和Matplotlib绘制参数方程定义的3D曲面

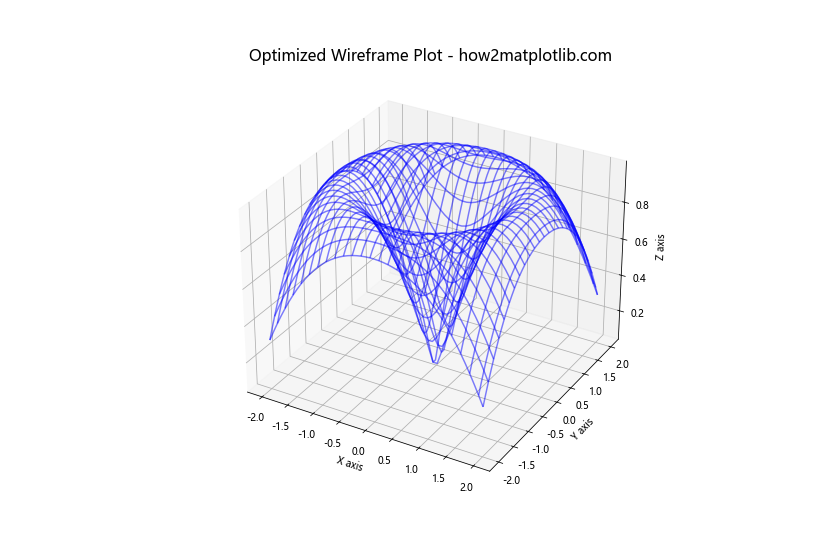
这个例子使用了线框图而不是实体曲面，并通过rstride和cstride参数减少了渲染的线条数量，从而提高了性能。

15. 总结

本文深入探讨了如何使用Python和Matplotlib绘制参数方程定义的3D曲面。我们从基本概念开始，逐步深入到更复杂的技术，包括自定义着色、添加交互性、结合其他图形元素等。通过这些示例，我们展示了Matplotlib强大的3D绘图能力，以及如何利用这些功能来创建丰富、直观的数据可视化。

3D曲面渲染是科学可视化和数据分析中的一个重要工具。它不仅可以帮助我们理解复杂的数学函数和物理现象，还可以用于展示各种实际应用中的数据，如地形建模、金融分析、工程设计等。

通过掌握本文介绍的技术，读者应该能够创建各种复杂的3D曲面图，并根据具体需求进行定制和优化。随着数据可视化在各个领域的重要性不断增加，这些技能将变得越来越有价值。

最后，值得注意的是，虽然Matplotlib提供了强大的3D绘图功能，但对于更复杂的3D渲染任务，可能需要考虑使用专门的3D图形库，如Mayavi或VTK。然而，对于大多数科学可视化和数据分析任务，Matplotlib的3D功能已经足够强大和灵活。

Camera课程

Camera API2 教程

API2 教程
Camera 性能教程

Perf 教程
Camera Native Framework 教程

Native FW 教程
Camera QCOM ISP 教程

ISP 教程
Camera QCOM Sensor 教程

Sensor 教程

Python教程

Python 教程

Python 教程
NumPy 教程

NumPy 教程
Django 教程

Django 教程

Java教程

Java 教程

Java 教程

Web教程

JavaScript 教程

JavaScript 教程
jQuery 教程

jQuery 教程
CSS 教程

CSS 教程
PHP 教程

PHP 教程
Laravel 教程

Laravel 教程
TypeScript 教程

TypeScript 教程
WordPress 教程

WordPress 教程

数据库教程

SQL 教程

SQL 教程
SQLite 教程

SQLite 教程
MySQL 教程

MySQL 教程
PL/SQL 教程

PL/SQL 教程
MongoDB 教程

MongoDB 教程

图形图像教程

OpenCV 教程

OpenCV 教程

办公软件教程

Excel 教程

Excel 教程

Linux教程

Linux命令全集

Linux命令全集
Linux内核API

Linux内核API
LVGL 教程

LVGL 教程

计算机教程

操作系统 教程

操作系统 教程
计算机网络 教程

计算机网络 教程
C语言 教程

C语言 教程
C++ 教程

C++ 教程
Swift 教程

Swift 教程

大数据教程

Hadoop 教程

Hadoop 教程
Spark 教程

Spark 教程
Scala 教程

Scala 教程

开发工具教程

Git 教程

Git 教程
Jenkins 教程

Jenkins 教程
ChatGPT 教程

ChatGPT 教程
IntelliJ 教程

IntelliJ 教程