Matplotlib.pyplot.yscale()：掌握Python中的y轴缩放技巧

Matplotlib.pyplot.yscale()：掌握Python中的y轴缩放技巧

参考：Matplotlib.pyplot.yscale() in Python

Matplotlib是Python中最流行的数据可视化库之一，它提供了丰富的绘图功能和自定义选项。在数据可视化过程中，合适的坐标轴缩放对于正确展示数据至关重要。本文将深入探讨Matplotlib.pyplot.yscale()函数，这是一个用于设置y轴缩放的强大工具。我们将详细介绍其用法、参数选项以及在不同场景下的应用，帮助你更好地掌握数据可视化技巧。

1. yscale()函数简介

yscale()函数是Matplotlib.pyplot模块中的一个重要函数，用于设置y轴的缩放方式。它允许我们改变y轴的刻度显示方式，以适应不同类型的数据分布。通过使用yscale()，我们可以轻松地在线性、对数、指数等不同的缩放方式之间切换，从而更好地展示数据的特征和趋势。

以下是一个简单的示例，展示了如何使用yscale()函数：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(0, 10, 100)
y = np.exp(x)

# 创建图形和坐标轴
plt.figure(figsize=(10, 6))

# 绘制数据
plt.plot(x, y, label='Exponential Growth')

# 设置y轴为对数缩放
plt.yscale('log')

# 添加标题和标签
plt.title('Exponential Growth with Log Scale (how2matplotlib.com)')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (log scale)')

# 添加图例
plt.legend()

# 显示网格
plt.grid(True)

# 显示图形
plt.show()

Output:

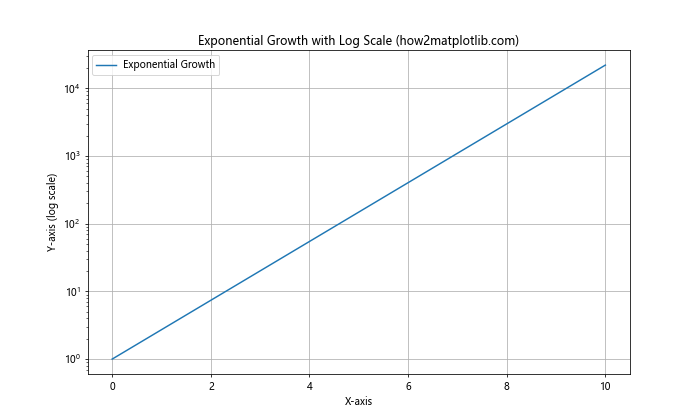
在这个示例中，我们绘制了一个指数增长的曲线，并使用plt.yscale('log')将y轴设置为对数缩放。这样可以更清晰地展示指数增长的特征，即使在数值范围很大的情况下也能看到曲线的变化趋势。

2. yscale()函数的参数

yscale()函数的基本语法如下：

matplotlib.pyplot.yscale(scale, **kwargs)

其中，主要参数包括：

1. scale：字符串，指定缩放类型。常用的选项包括：
   • ‘linear’：线性缩放（默认）
   • ‘log’：对数缩放
   • ‘symlog’：对称对数缩放
   • ‘logit’：logit缩放
   • ‘function’：自定义函数缩放
2. **kwargs：可选的关键字参数，用于进一步自定义缩放行为。

接下来，我们将详细介绍每种缩放类型的使用方法和适用场景。

3. 线性缩放（Linear Scale）

线性缩放是最常见的缩放方式，也是yscale()函数的默认选项。在线性缩放下，y轴上的刻度间隔保持恒定。这种缩放方式适用于大多数数据集，特别是当数据范围相对较小或者需要直观比较数值大小时。

以下是一个使用线性缩放的示例：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(0, 10, 100)
y = 2 * x + 1

# 创建图形和坐标轴
plt.figure(figsize=(10, 6))

# 绘制数据
plt.plot(x, y, label='Linear Function')

# 设置y轴为线性缩放（默认）
plt.yscale('linear')

# 添加标题和标签
plt.title('Linear Function with Linear Scale (how2matplotlib.com)')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (linear scale)')

# 添加图例
plt.legend()

# 显示网格
plt.grid(True)

# 显示图形
plt.show()

Output:

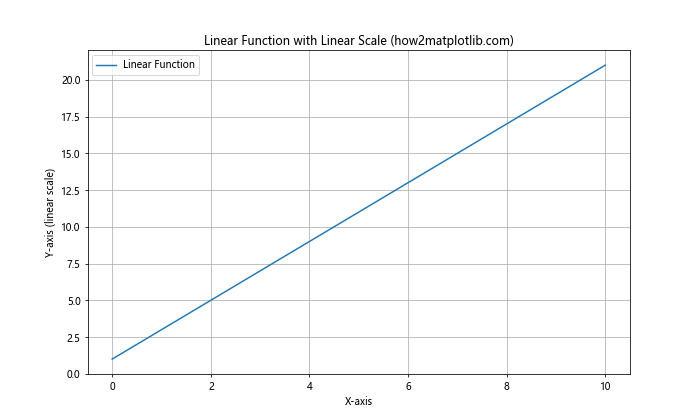
在这个例子中，我们绘制了一个简单的线性函数。虽然plt.yscale('linear')是默认设置，我们仍然显式地指定了它，以强调我们正在使用线性缩放。这种缩放方式使得函数的斜率在整个图表中保持一致，便于观察线性关系。

4. 对数缩放（Log Scale）

对数缩放在处理跨越多个数量级的数据时非常有用。它可以将乘法关系转换为加法关系，使得大范围的数据更容易在同一个图表中显示。对数缩放常用于金融、科学和工程领域，特别是在处理指数增长或衰减的数据时。

以下是一个使用对数缩放的示例：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(1, 1000, 1000)
y = x ** 2

# 创建图形和坐标轴
plt.figure(figsize=(10, 6))

# 绘制数据
plt.plot(x, y, label='Quadratic Function')

# 设置y轴为对数缩放
plt.yscale('log')

# 添加标题和标签
plt.title('Quadratic Function with Log Scale (how2matplotlib.com)')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (log scale)')

# 添加图例
plt.legend()

# 显示网格
plt.grid(True)

# 显示图形
plt.show()

Output:

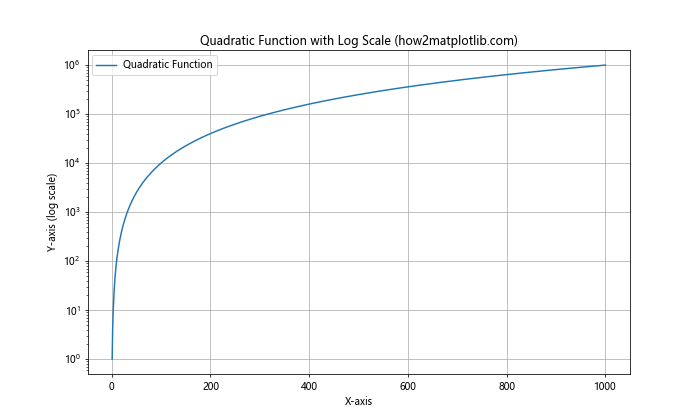
在这个例子中，我们绘制了一个二次函数。通过使用对数缩放，我们可以清楚地看到函数在整个范围内的变化趋势，即使y值跨越了多个数量级。

5. 对称对数缩放（Symlog Scale）

对称对数缩放是对数缩放的一种变体，它可以处理包含零和负值的数据。在常规对数缩放中，零和负值是无法表示的。对称对数缩放在零附近使用线性缩放，而在远离零的区域使用对数缩放，从而实现了对正负值的平滑过渡。

以下是一个使用对称对数缩放的示例：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(-100, 100, 1000)
y = x ** 3

# 创建图形和坐标轴
plt.figure(figsize=(10, 6))

# 绘制数据
plt.plot(x, y, label='Cubic Function')

# 设置y轴为对称对数缩放
plt.yscale('symlog', linthresh=10)

# 添加标题和标签
plt.title('Cubic Function with Symlog Scale (how2matplotlib.com)')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (symlog scale)')

# 添加图例
plt.legend()

# 显示网格
plt.grid(True)

# 显示图形
plt.show()

Output:

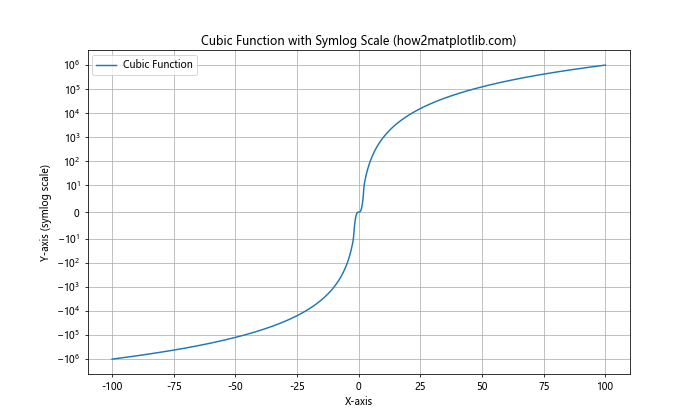
在这个例子中，我们绘制了一个立方函数，其中包含正值和负值。通过使用对称对数缩放，我们可以在一个图表中清晰地显示函数在正负区间的行为。linthresh参数定义了线性区域的范围，在这个例子中设置为10。

6. Logit缩放（Logit Scale）

Logit缩放主要用于处理概率数据，特别是在范围(0, 1)内的数据。它将概率值映射到整个实数轴，使得接近0和1的概率值更容易区分。Logit缩放在统计学和机器学习中经常用于可视化逻辑回归的结果。

以下是一个使用Logit缩放的示例：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(0.01, 0.99, 100)
y = 1 / (1 + np.exp(-10 * (x - 0.5)))

# 创建图形和坐标轴
plt.figure(figsize=(10, 6))

# 绘制数据
plt.plot(x, y, label='Sigmoid Function')

# 设置y轴为logit缩放
plt.yscale('logit')

# 添加标题和标签
plt.title('Sigmoid Function with Logit Scale (how2matplotlib.com)')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (logit scale)')

# 添加图例
plt.legend()

# 显示网格
plt.grid(True)

# 显示图形
plt.show()

Output:

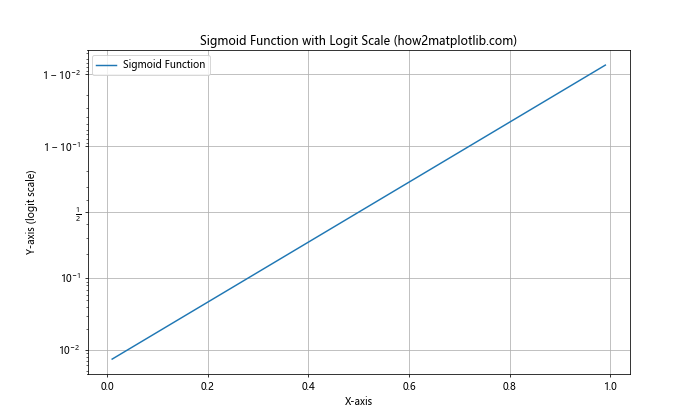
在这个例子中，我们绘制了一个sigmoid函数，它的值范围在0到1之间。通过使用logit缩放，我们可以更清楚地看到函数在接近0和1时的行为。

7. 自定义函数缩放（Function Scale）

除了内置的缩放选项，Matplotlib还允许我们使用自定义函数来定义缩放方式。这为处理特殊的数据分布提供了极大的灵活性。要使用自定义函数缩放，我们需要定义一个前向变换函数和一个反向变换函数。

以下是一个使用自定义函数缩放的示例：

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.scale import FuncScale
from matplotlib.transforms import FuncTransform

# 定义自定义缩放函数
def forward(x):
    return np.sqrt(x)

def inverse(x):
    return x ** 2

# 创建自定义缩放对象
scale = FuncScale(plt.gca(), (forward, inverse))

# 生成数据
x = np.linspace(0, 100, 1000)
y = x ** 2

# 创建图形和坐标轴
plt.figure(figsize=(10, 6))

# 绘制数据
plt.plot(x, y, label='Quadratic Function')

# 设置y轴为自定义函数缩放
plt.gca().set_yscale(scale)

# 添加标题和标签
plt.title('Quadratic Function with Custom Scale (how2matplotlib.com)')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (custom scale)')

# 添加图例
plt.legend()

# 显示网格
plt.grid(True)

# 显示图形
plt.show()

在这个例子中，我们定义了一个平方根缩放函数。这种缩放方式可以在某些情况下比对数缩放更适合，例如当数据增长速度介于线性和对数之间时。

8. 多子图中的yscale()应用

在复杂的数据可视化任务中，我们经常需要在一个图形中绘制多个子图，每个子图可能需要不同的y轴缩放方式。Matplotlib允许我们为每个子图单独设置yscale()。

以下是一个在多子图中应用不同yscale()的示例：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(0, 10, 100)
y1 = np.exp(x)
y2 = x ** 2
y3 = np.sin(x)

# 创建图形和子图
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(10, 15))

# 子图1：对数缩放
ax1.plot(x, y1, label='Exponential')
ax1.set_yscale('log')
ax1.set_title('Exponential Function (Log Scale)')
ax1.set_ylabel('Y-axis (log)')
ax1.legend()

# 子图2：线性缩放
ax2.plot(x, y2, label='Quadratic')
ax2.set_yscale('linear')
ax2.set_title('Quadratic Function (Linear Scale)')
ax2.set_ylabel('Y-axis (linear)')
ax2.legend()

# 子图3：对称对数缩放
ax3.plot(x, y3, label='Sine')
ax3.set_yscale('symlog', linthresh=0.1)
ax3.set_title('Sine Function (Symlog Scale)')
ax3.set_ylabel('Y-axis (symlog)')
ax3.legend()

# 调整子图间距
plt.tight_layout()

# 添加总标题
fig.suptitle('Multiple Scales in Subplots (how2matplotlib.com)', fontsize=16)

# 显示图形
plt.show()

Output:

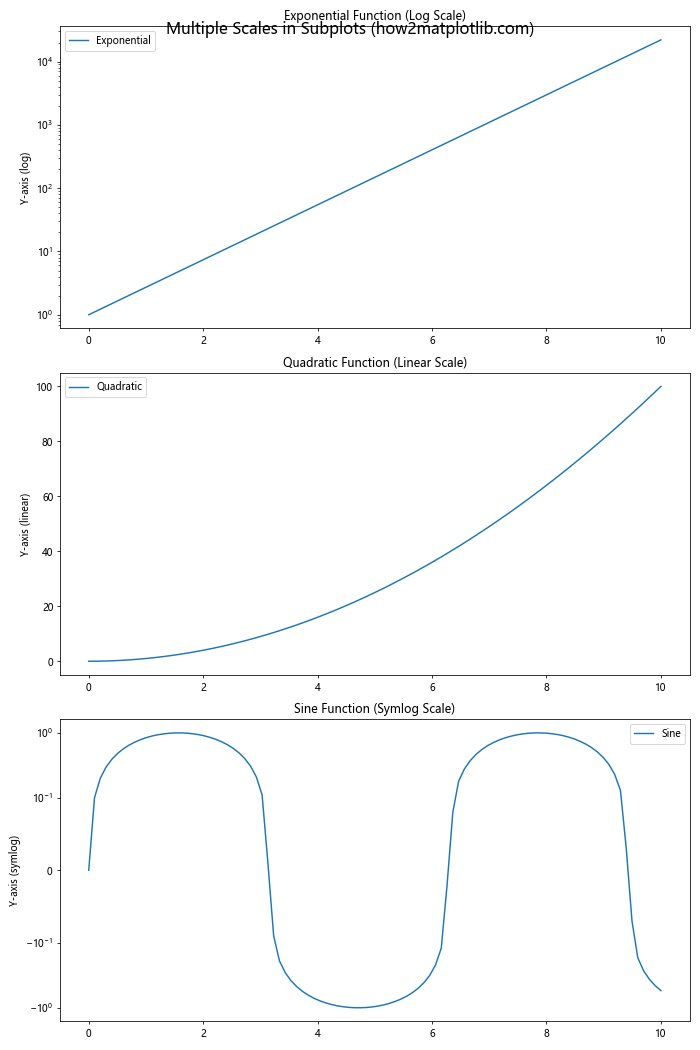
在这个例子中，我们创建了三个子图，分别使用了对数缩放、线性缩放和对称对数缩放。这种方法允许我们在一个图形中比较不同类型的数据分布，每种分布都使用最适合的缩放方式。

9. 动态调整yscale()

在某些情况下，我们可能需要根据用户输入或数据特征动态调整y轴的缩放方式。Matplotlib允许我们在运行时更改yscale()，这为交互式数据可视化提供了可能性。

以下是一个动态调整yscale()的示例：

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.widgets import RadioButtons

# 生成数据
x = np.linspace(0.1, 10, 100)
y = x ** 2

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(10, 6))
line, = ax.plot(x, y, label='Quadratic Function')

# 初始设置
ax.set_title('Quadratic Function (how2matplotlib.com)')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.legend()

# 创建单选按钮
rax = plt.axes([0.05, 0.7, 0.15, 0.15])
radio = RadioButtons(rax, ('linear', 'log', 'symlog'))

# 定义更新函数
def scale_function(label):
    ax.set_yscale(label)
    plt.draw()

# 连接单选按钮事件
radio.on_clicked(scale_function)

# 显示图形
plt.show()

Output:

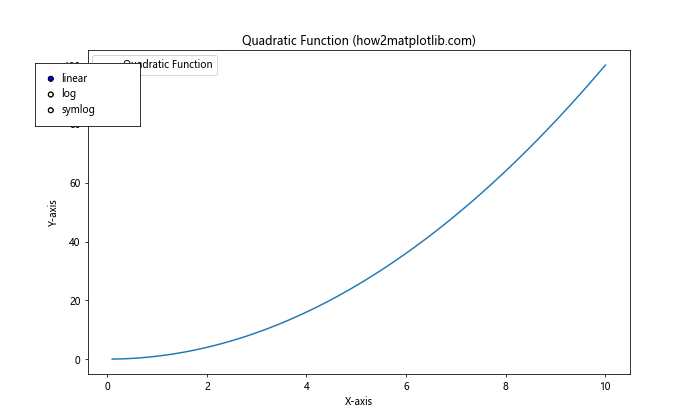
在这个例子中，我们创建了一个带有单选按钮的交互式图形。用户可以通过点击按钮来切换y轴的缩放方式，图形会实时更新以反映新的缩放设置。这种方法特别适用于探索性数据分析，允许用户快速尝试不同的缩放选项以找到最佳的数据表示方式。

10. yscale()与其他绘图元素的结合

yscale()函数通常不是孤立使用的，而是与其他Matplotlib功能结合使用，以创建更丰富、更有信息量的可视化效果。以下我们将探讨如何将yscale()与其他绘图元素结合使用。

10.1 结合颜色映射

将yscale()与颜色映射结合使用可以在一个图表中同时展示多个维度的信息。以下是一个示例：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(0.1, 10, 100)
y = np.exp(x)

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制数据，使用颜色映射
scatter = ax.scatter(x, y, c=y, cmap='viridis', s=50)

# 设置y轴为对数缩放
ax.set_yscale('log')

# 添加颜色条
plt.colorbar(scatter)

# 设置标题和标签
ax.set_title('Exponential Function with Color Mapping (how2matplotlib.com)')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (log scale)')

# 显示网格
ax.grid(True)

# 显示图形
plt.show()

Output:

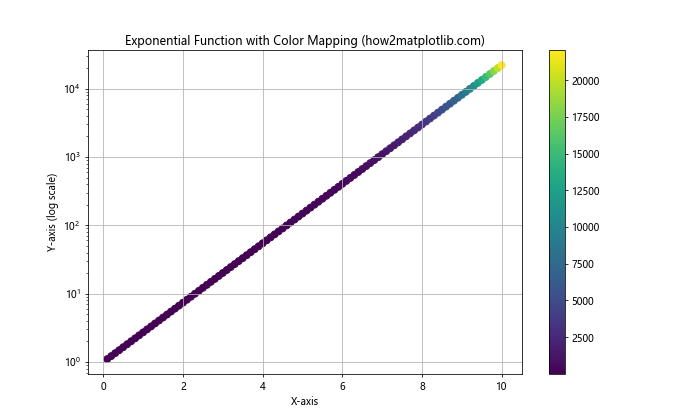
在这个例子中，我们使用散点图来表示指数函数，并使用颜色映射来表示y值的大小。通过结合对数缩放，我们可以清晰地看到函数值的变化趋势，同时颜色变化也直观地展示了数值的增长。

10.2 结合误差线

在科学和工程领域，数据点通常伴随着误差范围。我们可以将yscale()与误差线结合使用，以正确表示对数尺度下的误差。

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(1, 10, 10)
y = np.exp(x)
yerr = y * 0.1  # 10%的误差

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制数据和误差线
ax.errorbar(x, y, yerr=yerr, fmt='o', capsize=5, label='Data with Error')

# 设置y轴为对数缩放
ax.set_yscale('log')

# 设置标题和标签
ax.set_title('Exponential Data with Error Bars (how2matplotlib.com)')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (log scale)')

# 添加图例
ax.legend()

# 显示网格
ax.grid(True)

# 显示图形
plt.show()

Output:

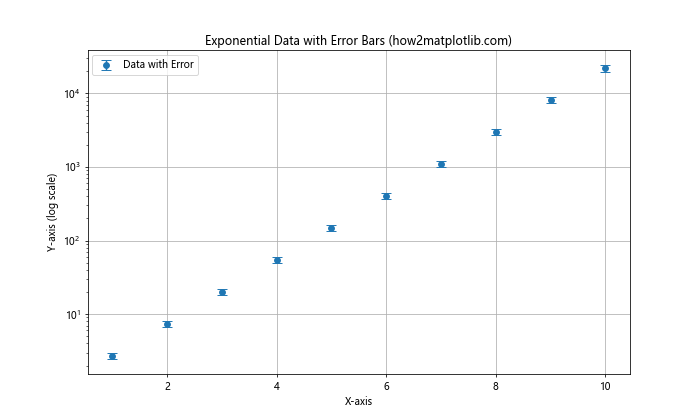
在这个例子中，我们绘制了带有误差线的指数数据。通过使用对数缩放，我们可以在大范围的y值中清晰地看到误差的相对大小。

10.3 结合双y轴

有时我们需要在同一个图表中显示具有不同数量级的两组数据。这时可以使用双y轴，并为每个y轴设置不同的缩放方式。

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(0, 10, 100)
y1 = np.exp(x)
y2 = x ** 2

# 创建图形和主坐标轴
fig, ax1 = plt.subplots(figsize=(10, 6))

# 绘制第一组数据
color = 'tab:blue'
ax1.set_xlabel('X-axis')
ax1.set_ylabel('Exponential', color=color)
ax1.plot(x, y1, color=color, label='Exponential')
ax1.tick_params(axis='y', labelcolor=color)
ax1.set_yscale('log')

# 创建次坐标轴
ax2 = ax1.twinx()

# 绘制第二组数据
color = 'tab:orange'
ax2.set_ylabel('Quadratic', color=color)
ax2.plot(x, y2, color=color, label='Quadratic')
ax2.tick_params(axis='y', labelcolor=color)
ax2.set_yscale('linear')

# 设置标题
fig.suptitle('Dual Y-axis with Different Scales (how2matplotlib.com)', fontsize=16)

# 添加图例
lines1, labels1 = ax1.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax1.legend(lines1 + lines2, labels1 + labels2, loc='upper left')

# 显示图形
plt.show()

Output:

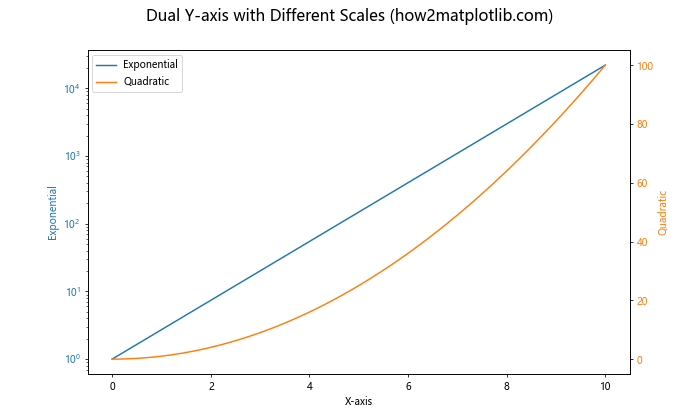
在这个例子中，我们在左侧y轴上使用对数缩放来显示指数函数，在右侧y轴上使用线性缩放来显示二次函数。这种方法允许我们在一个图表中比较不同量级和不同增长速度的数据。

11. yscale()的高级应用

除了基本用法外，yscale()还有一些高级应用，可以进一步增强数据可视化的效果和信息量。

11.1 自定义刻度标签

当使用非线性缩放时，有时默认的刻度标签可能不够直观。我们可以自定义刻度标签来提高可读性。

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(0, 5, 100)
y = np.exp(x)

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制数据
ax.plot(x, y, label='Exponential Growth')

# 设置y轴为对数缩放
ax.set_yscale('log')

# 自定义y轴刻度标签
y_ticks = [1, 10, 100, 1000]
ax.set_yticks(y_ticks)
ax.set_yticklabels([f'{tick:,}' for tick in y_ticks])

# 设置标题和标签
ax.set_title('Exponential Growth with Custom Tick Labels (how2matplotlib.com)')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (log scale)')

# 添加图例
ax.legend()

# 显示网格
ax.grid(True)

# 显示图形
plt.show()

Output:

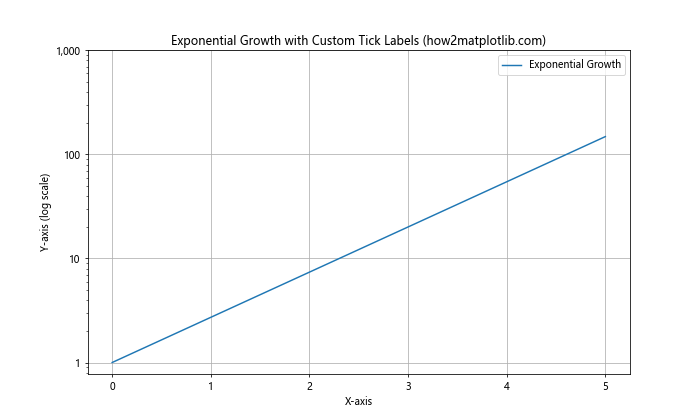
在这个例子中，我们自定义了y轴的刻度标签，使用逗号分隔符来提高大数字的可读性。

11.2 非均匀刻度

在某些情况下，我们可能需要非均匀的刻度来更好地展示数据。Matplotlib允许我们创建自定义的刻度定位器来实现这一点。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import FixedLocator, ScalarFormatter

# 生成数据
x = np.linspace(0, 10, 100)
y = np.exp(x)

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制数据
ax.plot(x, y, label='Exponential Growth')

# 设置y轴为对数缩放
ax.set_yscale('log')

# 创建非均匀刻度
y_ticks = [1, 5, 10, 50, 100, 500, 1000, 5000, 10000]
ax.yaxis.set_major_locator(FixedLocator(y_ticks))
ax.yaxis.set_major_formatter(ScalarFormatter())

# 设置标题和标签
ax.set_title('Exponential Growth with Non-uniform Ticks (how2matplotlib.com)')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (log scale)')

# 添加图例
ax.legend()

# 显示网格
ax.grid(True)

# 显示图形
plt.show()

Output:

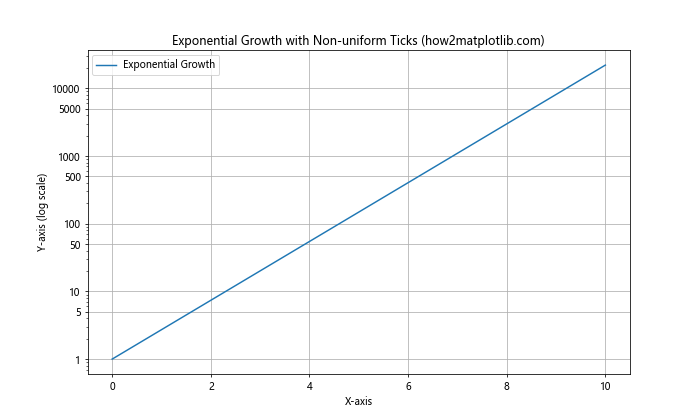
在这个例子中，我们创建了一个非均匀的刻度序列，包括一些中间值，以便更好地展示数据的变化。

11.3 对数刻度的底数调整

默认情况下，Matplotlib的对数刻度使用以10为底的对数。但在某些情况下，使用其他底数可能更合适。我们可以通过设置base参数来调整对数的底数。

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(1, 10, 100)
y = 2 ** x

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制数据
ax.plot(x, y, label='Exponential Growth (base 2)')

# 设置y轴为以2为底的对数缩放
ax.set_yscale('log', base=2)

# 设置标题和标签
ax.set_title('Exponential Growth with Base-2 Log Scale (how2matplotlib.com)')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (log2 scale)')

# 添加图例
ax.legend()

# 显示网格
ax.grid(True)

# 显示图形
plt.show()

Output:

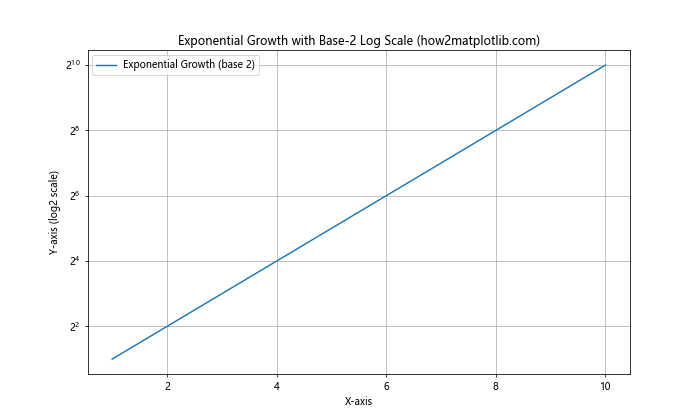
在这个例子中，我们使用以2为底的对数刻度来展示2的幂函数。这种方法在处理计算机科学相关数据时特别有用，因为许多计算机相关的量都是2的幂。

12. yscale()在数据分析中的应用

yscale()函数不仅仅是一个绘图工具，它在数据分析过程中也扮演着重要角色。通过改变数据的表示方式，我们可以揭示隐藏在原始数据中的模式和关系。

12.1 识别幂律关系

在许多自然和社会现象中，我们经常遇到幂律关系。使用对数刻度可以帮助我们识别这种关系。

import matplotlib.pyplot as plt
import numpy as np

# 生成幂律数据
x = np.logspace(0, 3, 100)
y = 5 * x ** (-1.5) + np.random.normal(0, 0.1, 100)

# 创建图形和坐标轴
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

# 线性刻度
ax1.scatter(x, y)
ax1.set_title('Power Law (Linear Scale)')
ax1.set_xlabel('X-axis')
ax1.set_ylabel('Y-axis')

# 对数刻度
ax2.scatter(x, y)
ax2.set_xscale('log')
ax2.set_yscale('log')
ax2.set_title('Power Law (Log-Log Scale)')
ax2.set_xlabel('X-axis (log)')
ax2.set_ylabel('Y-axis (log)')

# 添加总标题
fig.suptitle('Identifying Power Law Relationships (how2matplotlib.com)', fontsize=16)

# 调整子图间距
plt.tight_layout()

# 显示图形
plt.show()

Output:

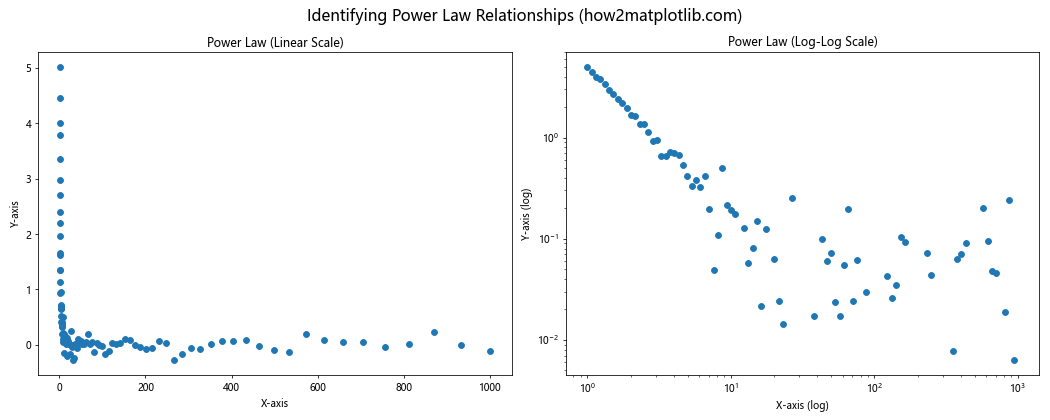
在这个例子中，我们生成了一个带有噪声的幂律数据。在线性刻度下，关系并不明显，但在对数-对数刻度下，幂律关系表现为一条直线，使得识别和分析变得更加容易。

12.2 处理长尾分布

许多现实世界的数据集呈现长尾分布，如收入分布、城市人口等。对数刻度可以帮助我们更好地可视化这类分布。

import matplotlib.pyplot as plt
import numpy as np

# 生成长尾分布数据
data = np.random.pareto(1, 1000) + 1

# 创建图形和坐标轴
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

# 线性刻度直方图
ax1.hist(data, bins=50)
ax1.set_title('Long-tail Distribution (Linear Scale)')
ax1.set_xlabel('Value')
ax1.set_ylabel('Frequency')

# 对数刻度直方图
ax2.hist(data, bins=50)
ax2.set_yscale('log')
ax2.set_title('Long-tail Distribution (Log Scale)')
ax2.set_xlabel('Value')
ax2.set_ylabel('Frequency (log)')

# 添加总标题
fig.suptitle('Visualizing Long-tail Distributions (how2matplotlib.com)', fontsize=16)

# 调整子图间距
plt.tight_layout()

# 显示图形
plt.show()

Output:

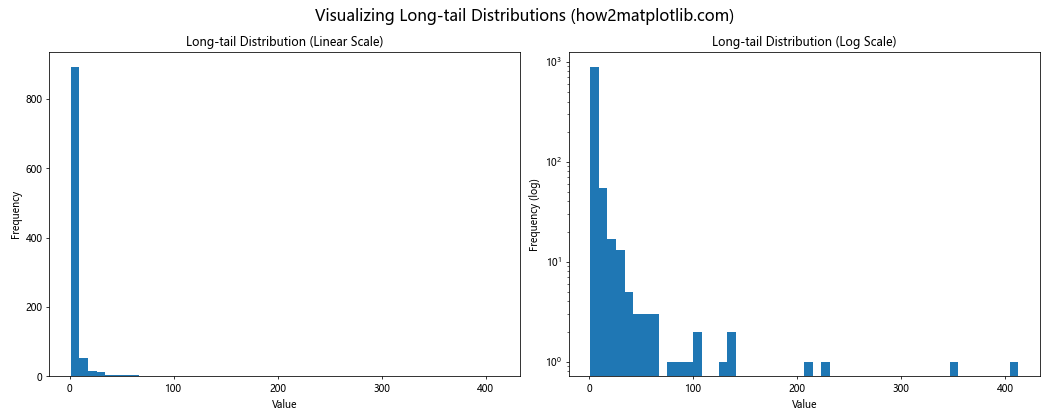
在这个例子中，我们生成了一个帕累托分布的数据集来模拟长尾分布。在线性刻度下，分布的长尾部分几乎不可见，而在对数刻度下，我们可以清楚地看到分布的全貌，包括那些频率较低但仍然重要的事件。

12.3 比较不同增长率

当比较具有不同增长率的数据时，对数刻度可以帮助我们更好地理解相对增长。

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x = np.linspace(0, 10, 100)
y1 = np.exp(0.5 * x)
y2 = np.exp(0.3 * x)
y3 = np.exp(0.1 * x)

# 创建图形和坐标轴
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

# 线性刻度
ax1.plot(x, y1, label='High Growth')
ax1.plot(x, y2, label='Medium Growth')
ax1.plot(x, y3, label='Low Growth')
ax1.set_title('Different Growth Rates (Linear Scale)')
ax1.set_xlabel('Time')
ax1.set_ylabel('Value')
ax1.legend()

# 对数刻度
ax2.plot(x, y1, label='High Growth')
ax2.plot(x, y2, label='Medium Growth')
ax2.plot(x, y3, label='Low Growth')
ax2.set_yscale('log')
ax2.set_title('Different Growth Rates (Log Scale)')
ax2.set_xlabel('Time')
ax2.set_ylabel('Value (log)')
ax2.legend()

# 添加总标题
fig.suptitle('Comparing Growth Rates (how2matplotlib.com)', fontsize=16)

# 调整子图间距
plt.tight_layout()

# 显示图形
plt.show()

Output:

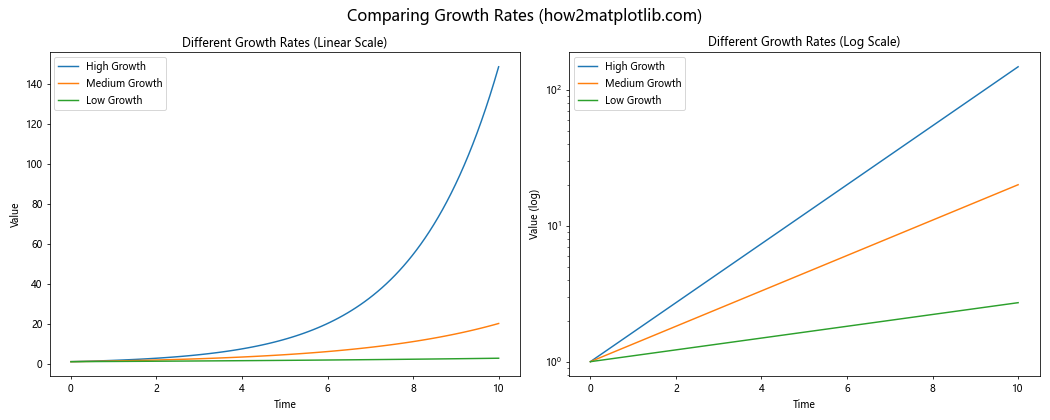
在这个例子中，我们比较了三种不同的指数增长率。在线性刻度下，低增长率的曲线几乎看不见，而在对数刻度下，我们可以清楚地看到所有三条曲线的相对增长情况。

13. yscale()在特定领域的应用

yscale()函数在许多特定领域都有重要应用。以下我们将探讨一些常见的应用场景。

13.1 金融数据分析

在金融领域，对数刻度常用于分析股票价格和市场指数的长期趋势。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

# 生成模拟的股票数据
dates = pd.date_range(start='2010-01-01', end='2020-12-31', freq='D')
price = 100 * (1 + np.random.normal(0, 0.01, len(dates))).cumprod()
data = pd.Series(price, index=dates)

# 创建图形和坐标轴
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10))

# 线性刻度
data.plot(ax=ax1)
ax1.set_title('Stock Price (Linear Scale)')
ax1.set_ylabel('Price')

# 对数刻度
data.plot(ax=ax2)
ax2.set_yscale('log')
ax2.set_title('Stock Price (Log Scale)')
ax2.set_ylabel('Price (log)')

# 添加总标题
fig.suptitle('Stock Price Analysis (how2matplotlib.com)', fontsize=16)

# 调整子图间距
plt.tight_layout()

# 显示图形
plt.show()

Output:

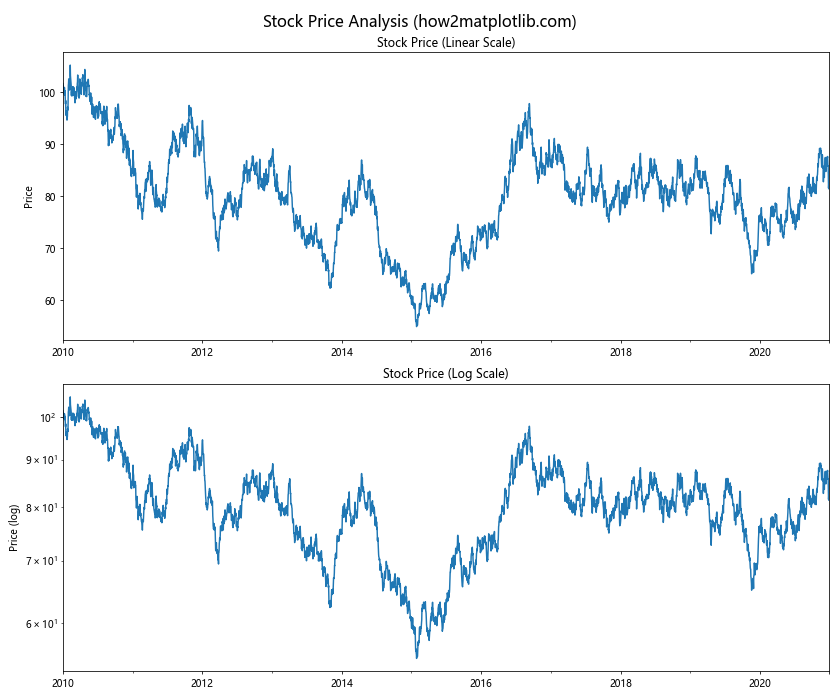
在这个例子中，我们模拟了10年的每日股票价格数据。对数刻度使得相对变化更加明显，有助于识别长期趋势和周期性模式。

13.2 科学数据可视化

在科学研究中，对数刻度常用于表示跨越多个数量级的数据，如天文学中的距离或物理学中的粒子能量。

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
masses = np.logspace(-30, 30, 61)  # 从亚原子粒子到天体的质量范围
labels = ['Electron', 'Proton', 'DNA Molecule', 'Bacteria', 'Human', 'Blue Whale', 'Earth', 'Sun']
masses_labeled = [9.1e-31, 1.67e-27, 1e-14, 1e-12, 70, 1.9e5, 5.97e24, 1.99e30]

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(12, 6))

# 绘制数据
ax.scatter(masses, np.ones_like(masses), s=50, alpha=0.5)
ax.scatter(masses_labeled, np.ones_like(masses_labeled), s=100, c='red', zorder=5)

# 添加标签
for mass, label in zip(masses_labeled, labels):
    ax.annotate(label, (mass, 1), xytext=(0, 10), 
                textcoords='offset points', ha='center', va='bottom',
                rotation=45)

# 设置x轴为对数刻度
ax.set_xscale('log')

# 设置y轴范围并移除刻度
ax.set_ylim(0.5, 1.5)
ax.set_yticks([])

# 设置标题和标签
ax.set_title('Mass Scale of the Universe (how2matplotlib.com)')
ax.set_xlabel('Mass (kg)')

# 显示网格
ax.grid(True, which='both', ls='-', alpha=0.2)

# 显示图形
plt.tight_layout()
plt.show()

Output:

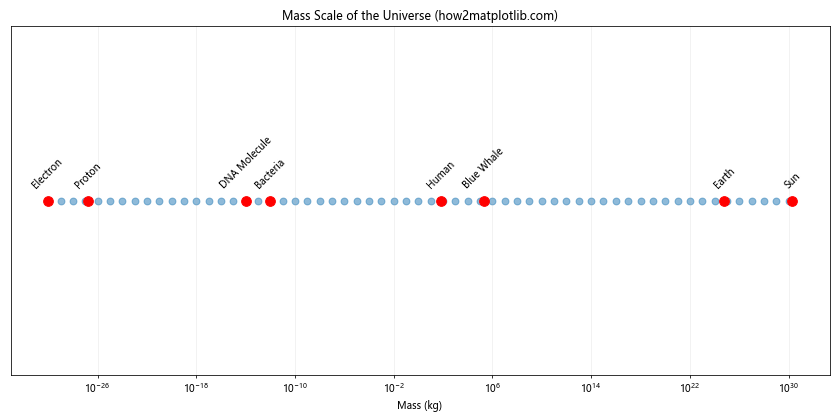
这个例子展示了从亚原子粒子到天体的质量范围，跨越了约60个数量级。使用对数刻度使我们能够在一个图表中直观地比较这些极其不同的质量。

13.3 人口统计学

在人口统计学中，对数刻度常用于比较不同规模的人口数据。

import matplotlib.pyplot as plt
import numpy as np

# 模拟数据
countries = ['China', 'India', 'USA', 'Indonesia', 'Pakistan', 'Brazil', 'Nigeria', 'Bangladesh', 'Russia', 'Mexico']
populations = [1439, 1380, 331, 273, 220, 212, 206, 164, 145, 128]  # 单位：百万

# 创建图形和坐标轴
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

# 线性刻度
ax1.bar(countries, populations)
ax1.set_title('Population by Country (Linear Scale)')
ax1.set_ylabel('Population (millions)')
ax1.tick_params(axis='x', rotation=45)

# 对数刻度
ax2.bar(countries, populations)
ax2.set_yscale('log')
ax2.set_title('Population by Country (Log Scale)')
ax2.set_ylabel('Population (log scale)')
ax2.tick_params(axis='x', rotation=45)

# 添加总标题
fig.suptitle('World Population Comparison (how2matplotlib.com)', fontsize=16)

# 调整子图间距
plt.tight_layout()

# 显示图形
plt.show()

Output:

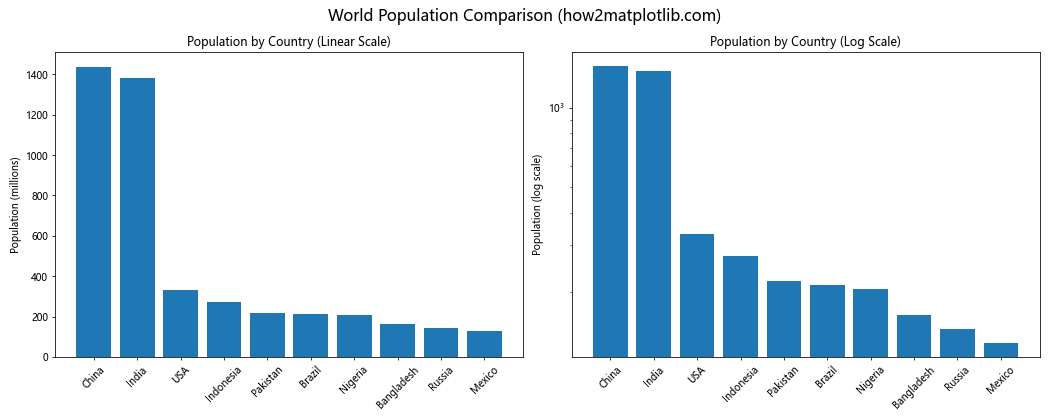
在这个例子中，我们比较了世界上人口最多的10个国家。对数刻度使得人口较少的国家的数据也能清晰可见，便于进行相对比较。

14. yscale()的常见问题和解决方案

在使用yscale()函数时，可能会遇到一些常见问题。以下是一些问题及其解决方案：

14.1 处理零值和负值

对数刻度无法处理零值和负值。当数据中包含这些值时，我们需要采取特殊措施。

import matplotlib.pyplot as plt
import numpy as np

# 生成包含零值和负值的数据
x = np.linspace(-10, 10, 100)
y = x ** 3

# 创建图形和坐标轴
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

# 使用symlog刻度
ax1.plot(x, y)
ax1.set_yscale('symlog', linthresh=1)
ax1.set_title('Cubic Function (Symlog Scale)')
ax1.set_xlabel('X-axis')
ax1.set_ylabel('Y-axis (symlog)')
ax1.grid(True)

# 使用函数变换
def func(x):
    return np.sign(x) * np.log1p(np.abs(x))

def inv_func(x):
    return np.sign(x) * (np.exp(np.abs(x)) - 1)

ax2.plot(x, y)
ax2.set_yscale('function', functions=(func, inv_func))
ax2.set_title('Cubic Function (Custom Log Scale)')
ax2.set_xlabel('X-axis')
ax2.set_ylabel('Y-axis (custom log)')
ax2.grid(True)

# 添加总标题
fig.suptitle('Handling Zero and Negative Values (how2matplotlib.com)', fontsize=16)

# 调整子图间距
plt.tight_layout()

# 显示图形
plt.show()

Output:

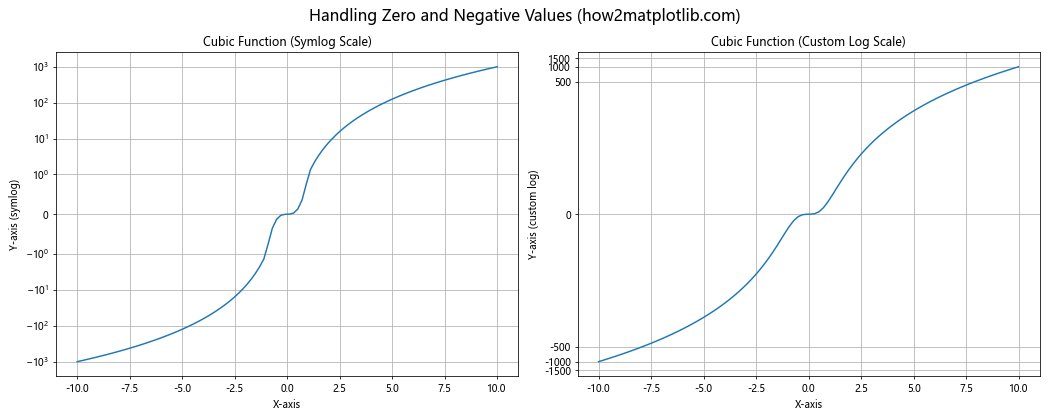
在这个例子中，我们使用了两种方法来处理包含零值和负值的数据：symlog刻度和自定义函数变换。symlog在零附近使用线性刻度，而在远离零的区域使用对数刻度。自定义函数变换则使用了一种可以处理负值的对数变换。

14.2 调整刻度密度

有时默认的刻度可能太稀疏或太密集。我们可以使用TickLocator和Formatter来调整刻度的密度和格式。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import LogLocator, LogFormatter

# 生成数据
x = np.logspace(0, 5, 100)
y = x ** 2

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(12, 6))

# 绘制数据
ax.plot(x, y)

# 设置对数刻度
ax.set_yscale('log')

# 调整刻度密度
ax.yaxis.set_major_locator(LogLocator(base=10, numticks=10))
ax.yaxis.set_minor_locator(LogLocator(base=10, subs=np.arange(2, 10) * 0.1, numticks=100))
ax.yaxis.set_major_formatter(LogFormatter(labelOnlyBase=False))

# 设置标题和标签
ax.set_title('Adjusting Tick Density in Log Scale (how2matplotlib.com)')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (log scale)')

# 显示网格
ax.grid(True, which='both', ls='-', alpha=0.2)

# 显示图形
plt.tight_layout()
plt.show()

Output:

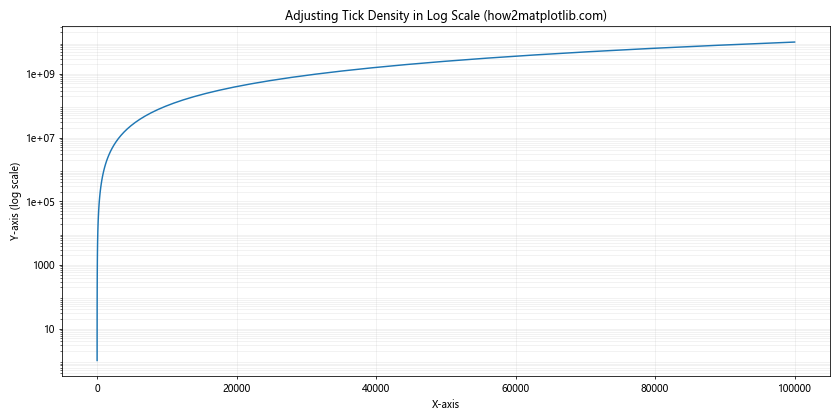
在这个例子中，我们使用LogLocator来设置主刻度和次刻度的位置，并使用LogFormatter来格式化刻度标签。这样可以得到更加精细和信息丰富的刻度。

14.3 处理大范围数据

当数据范围非常大时，即使使用对数刻度也可能难以清晰地显示所有数据。在这种情况下，我们可以考虑使用分段的对数刻度或自定义的非线性变换。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.scale import FuncScale
from matplotlib.transforms import FuncTransform

# 定义自定义变换函数
def forward(x):
    return np.sign(x) * np.log1p(np.abs(x))

def inverse(x):
    return np.sign(x) * (np.exp(np.abs(x)) - 1)

# 创建自定义刻度
scale = FuncScale(plt.gca(), (forward, inverse))

# 生成大范围数据
x = np.linspace(0, 1e10, 1000)
y = x ** 2

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(12, 6))

# 绘制数据
ax.plot(x, y)

# 应用自定义刻度
ax.set_yscale(scale)

# 设置标题和标签
ax.set_title('Handling Large Range Data (how2matplotlib.com)')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (custom scale)')

# 显示网格
ax.grid(True)

# 显示图形
plt.tight_layout()
plt.show()

在这个例子中，我们定义了一个自定义的非线性变换函数，它在保持单调性的同时，可以更好地处理大范围的数据。这种方法可以在不失去数据细节的情况下，展示跨越多个数量级的数据。

15. 结论

Matplotlib.pyplot.yscale()函数是一个强大的工具，可以帮助我们更好地可视化和分析各种类型的数据。通过选择适当的缩放方式，我们可以揭示数据中隐藏的模式和关系，使得复杂的数据集变得更加易于理解和解释。

在本文中，我们详细探讨了yscale()函数的各种用法，包括线性、对数、对称对数、logit和自定义函数缩放。我们还讨论了如何将yscale()与其他Matplotlib功能结合使用，以创建更丰富、更有信息量的可视化效果。

通过实际的例子，我们展示了yscale()在金融、科学、人口统计学等领域的应用，以及如何处理常见的问题，如零值和负值、刻度密度调整和大范围数据的处理。

掌握yscale()函数的使用不仅可以提高我们的数据可视化技能，还能帮助我们更深入地理解和分析数据。在数据科学和科学研究中，选择合适的坐标轴缩放方式往往是揭示数据本质和得出正确结论的关键步骤。

随着数据可视化在各个领域的重要性日益增加，熟练运用yscale()等Matplotlib功能将成为数据分析师、科研人员和工程师的必备技能。我们鼓励读者在实际项目中尝试使用不同的缩放方式，探索数据的多个方面，从而获得更全面、更深入的洞察。

最后，需要强调的是，虽然yscale()是一个强大的工具，但它并不是万能的。在使用时，我们应该始终考虑数据的本质和我们想要传达的信息。有时，最简单的线性缩放可能是最好的选择；而在其他情况下，复杂的非线性变换可能是必要的。关键是要根据具体情况选择最合适的方法，并确保我们的可视化既准确又易于理解。