如何在Matplotlib中绘制线性回归的最佳拟合线|极客笔记

如何在Matplotlib中绘制线性回归的最佳拟合线

在数据可视化中，线性回归是一种常用的方法，用来找出数据中的趋势线，也就是所谓的“最佳拟合线”。在Matplotlib中，我们可以使用numpy和matplotlib.pyplot库来实现线性回归并画出最佳拟合线。下面将详细介绍如何在Matplotlib中绘制线性回归的最佳拟合线。

示例代码1：生成随机数据

import numpy as np

# 生成随机数据
np.random.seed(0)
x = np.random.rand(100) * 10
y = 2 * x + 1 + np.random.randn(100)

print(x[:5], y[:5])

Output:

如何在Matplotlib中绘制线性回归的最佳拟合线

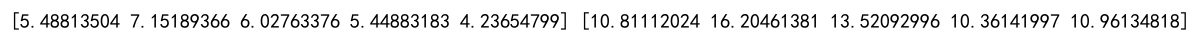
示例代码2：绘制散点图

import matplotlib.pyplot as plt

# 绘制散点图
plt.scatter(x, y)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Scatter Plot')
plt.show()

示例代码3：计算最佳拟合线

from numpy.polynomial.polynomial import polyfit

# 计算最佳拟合线
b, m = polyfit(x, y, 1)

print('斜率m:', m)
print('截距b:', b)

示例代码4：绘制最佳拟合线

import matplotlib.pyplot as plt

# 绘制最佳拟合线
plt.scatter(x, y)
plt.plot(x, m*x + b, color='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Line of Best Fit')
plt.show()

通过上面的示例代码，我们成功地利用Matplotlib绘制出了包含散点和最佳拟合线的图像。接下来，我们将继续探讨线性回归的更多用法。

示例代码5：线性回归预测

# 预测新数据点
x_new = 5
y_pred = m * x_new + b

print('预测值:', y_pred)

示例代码6：计算回归系数

from scipy.stats import linregress

# 计算回归系数
slope, intercept, r_value, p_value, std_err = linregress(x, y)

print('斜率:', slope)
print('截距:', intercept)
print('R平方:', r_value**2)

示例代码7：绘制回归直线

import matplotlib.pyplot as plt

# 绘制回归直线
plt.scatter(x, y)
plt.plot(x, slope*x + intercept, color='green')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Regression Line')
plt.show()

除了简单的线性回归之外，我们还可以尝试多项式回归来拟合数据中的曲线。下面是一个多项式回归的示例。

示例代码8：多项式回归

import numpy as np

# 生成随机数据
x = np.linspace(-5, 5, 100)
y = 2*x**3 - 3*x**2 + 2*x + 1 + np.random.randn(100)

# 计算多项式拟合线
p = np.polyfit(x, y, 3)

print('多项式系数:', p)

Output:

如何在Matplotlib中绘制线性回归的最佳拟合线

示例代码9：绘制多项式拟合线

import matplotlib.pyplot as plt
import numpy as np

# 绘制多项式拟合线
plt.scatter(x, y)
plt.plot(x, np.polyval(p, x), color='purple')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Polynomial Regression')
plt.show()

通过上面的示例代码，我们成功地实现了多项式回归并绘制出了拟合线。最后，我们还可以计算拟合线的预测误差，来评估拟合线的拟合程度。

示例代码10：计算预测误差

from sklearn.metrics import mean_squared_error
import numpy as np

# 计算预测误差
y_pred = np.polyval(p, x)
mse = mean_squared_error(y, y_pred)

print('平均方差:', mse)

以上就是关于在Matplotlib中绘制最佳拟合线的详细介绍和示例代码。通过线性回归和多项式回归，我们可以更好地理解数据中的趋势和关系。在实际应用中，我们可以根据需求选择不同的拟合方法来实现数据的最佳拟合和预测。Matplotlib提供了丰富的可视化功能，帮助我们更直观地展示数据和结果。