Matplotlib中如何将Y轴设置为对数刻度
参考:How to put the y-axis in logarithmic scale with Matplotlib
Matplotlib是Python中最流行的数据可视化库之一,它提供了丰富的绘图功能和灵活的自定义选项。在数据分析和科学研究中,我们经常需要处理跨越多个数量级的数据。在这种情况下,使用对数刻度可以更好地展示数据的分布和变化趋势。本文将详细介绍如何在Matplotlib中将Y轴设置为对数刻度,并提供多个实用示例。
1. 为什么使用对数刻度?
在开始学习如何设置对数刻度之前,我们先来了解为什么要使用对数刻度。对数刻度在以下情况下特别有用:
- 数据跨越多个数量级
- 需要展示指数增长或衰减的趋势
- 想要突出显示小数值的变化
- 处理幂律分布的数据
使用对数刻度可以帮助我们更好地可视化和理解这些类型的数据。
2. 基本方法:使用plt.yscale(‘log’)
设置Y轴为对数刻度的最简单方法是使用plt.yscale('log')函数。这个方法适用于大多数简单的绘图需求。
以下是一个基本示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
x = np.linspace(1, 10, 100)
y = np.exp(x)
# 创建图形
plt.figure(figsize=(10, 6))
plt.plot(x, y, label='Exponential Growth')
plt.title('Exponential Growth - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (log scale)')
# 设置Y轴为对数刻度
plt.yscale('log')
plt.legend()
plt.grid(True)
plt.show()
Output:
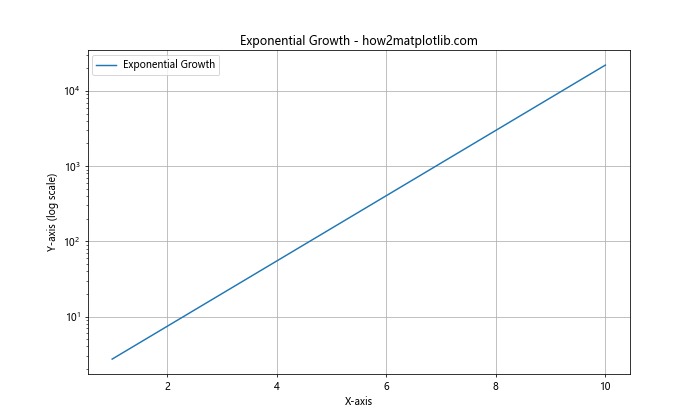
在这个例子中,我们绘制了一个指数增长的曲线。通过使用plt.yscale('log'),我们将Y轴设置为对数刻度,使得指数增长的趋势在图表中更加清晰可见。
3. 使用semilogx()和semilogy()函数
Matplotlib提供了两个专门用于创建半对数图的函数:semilogx()和semilogy()。这些函数分别用于创建X轴为对数刻度和Y轴为对数刻度的图形。
以下是使用semilogy()的示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
x = np.linspace(0, 5, 100)
y = np.exp(x)
# 创建半对数图
plt.figure(figsize=(10, 6))
plt.semilogy(x, y, label='Exponential Growth')
plt.title('Exponential Growth (Semilogy) - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (log scale)')
plt.legend()
plt.grid(True)
plt.show()
Output:
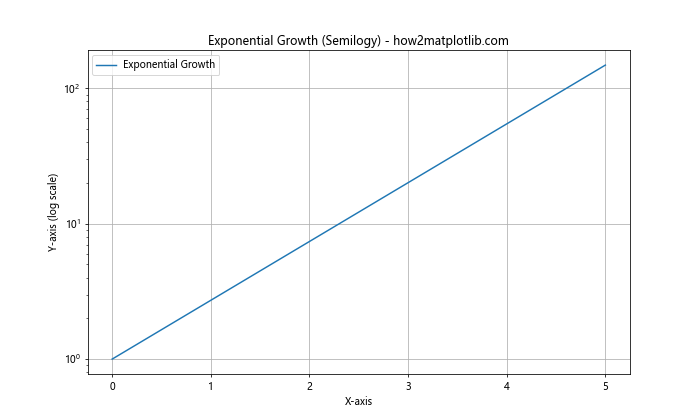
这个例子与前一个类似,但我们使用了plt.semilogy()函数来创建Y轴为对数刻度的图形。这种方法更加直观,特别是当你只需要Y轴为对数刻度时。
4. 在子图中设置对数刻度
当你需要在一个图形中创建多个子图,并且只想将其中一些子图的Y轴设置为对数刻度时,可以使用ax.set_yscale('log')方法。
以下是一个包含两个子图的示例,其中一个使用线性刻度,另一个使用对数刻度:
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
x = np.linspace(0, 10, 100)
y1 = x**2
y2 = np.exp(x)
# 创建包含两个子图的图形
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# 第一个子图:线性刻度
ax1.plot(x, y1, label='Quadratic')
ax1.set_title('Linear Scale - how2matplotlib.com')
ax1.set_xlabel('X-axis')
ax1.set_ylabel('Y-axis')
ax1.legend()
ax1.grid(True)
# 第二个子图:对数刻度
ax2.plot(x, y2, label='Exponential')
ax2.set_title('Log Scale - how2matplotlib.com')
ax2.set_xlabel('X-axis')
ax2.set_ylabel('Y-axis (log scale)')
ax2.set_yscale('log')
ax2.legend()
ax2.grid(True)
plt.tight_layout()
plt.show()
Output:
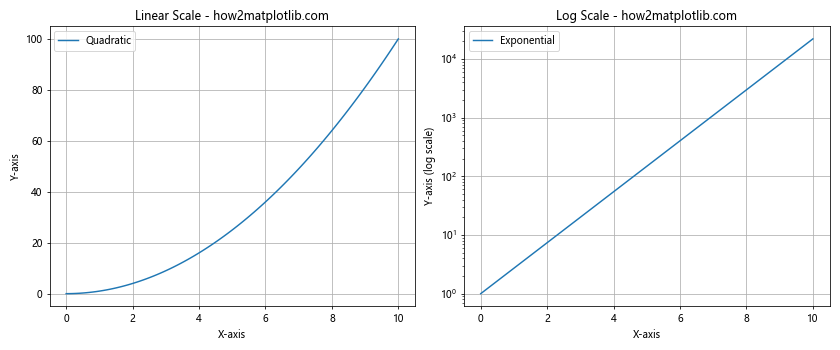
在这个例子中,我们创建了两个子图。左侧子图使用线性刻度显示二次函数,右侧子图使用对数刻度显示指数函数。通过比较这两个图,我们可以清楚地看到对数刻度如何帮助我们更好地可视化快速增长的数据。
5. 自定义对数刻度的底数
默认情况下,Matplotlib使用以10为底的对数刻度。但有时候,我们可能需要使用其他底数,如自然对数(以e为底)或以2为底的对数。我们可以通过设置base参数来实现这一点。
以下是一个使用不同底数的示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
x = np.linspace(1, 10, 100)
y = np.exp(x)
# 创建包含三个子图的图形
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5))
# 底数为10的对数刻度
ax1.semilogy(x, y, base=10)
ax1.set_title('Base 10 - how2matplotlib.com')
ax1.set_xlabel('X-axis')
ax1.set_ylabel('Y-axis (log10 scale)')
ax1.grid(True)
# 底数为e的对数刻度
ax2.semilogy(x, y, base=np.e)
ax2.set_title('Base e - how2matplotlib.com')
ax2.set_xlabel('X-axis')
ax2.set_ylabel('Y-axis (ln scale)')
ax2.grid(True)
# 底数为2的对数刻度
ax3.semilogy(x, y, base=2)
ax3.set_title('Base 2 - how2matplotlib.com')
ax3.set_xlabel('X-axis')
ax3.set_ylabel('Y-axis (log2 scale)')
ax3.grid(True)
plt.tight_layout()
plt.show()
Output:
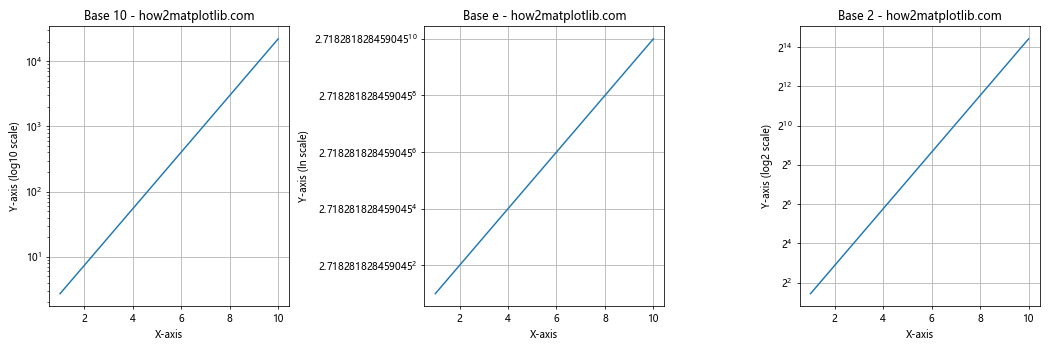
这个例子展示了如何使用不同的底数(10、e和2)来创建对数刻度。通过比较这三个图,我们可以看到不同底数对数刻度的影响。
6. 设置对数刻度的范围
有时,我们可能需要限制对数刻度的范围。这可以通过设置Y轴的限制来实现。以下是一个示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
x = np.linspace(0, 5, 100)
y = np.exp(x)
# 创建图形
plt.figure(figsize=(10, 6))
plt.semilogy(x, y, label='Exponential Growth')
plt.title('Limited Log Scale Range - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (log scale)')
# 设置Y轴的范围
plt.ylim(1, 100)
plt.legend()
plt.grid(True)
plt.show()
Output:
在这个例子中,我们使用plt.ylim(1, 100)将Y轴的范围限制在1到100之间。这对于聚焦于数据的特定部分非常有用。
7. 处理负值和零值
对数刻度通常只适用于正数。然而,在某些情况下,我们可能需要处理包含负值或零值的数据。Matplotlib提供了一些选项来处理这种情况。
7.1 使用SymLogNorm
SymLogNorm允许我们在对数刻度中包含负值和零值。以下是一个示例:
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import SymLogNorm
# 生成包含负值的数据
x = np.linspace(-10, 10, 100)
y = x**3
# 创建图形
plt.figure(figsize=(10, 6))
plt.plot(x, y)
plt.title('Symmetric Log Scale - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (symlog scale)')
# 使用SymLogNorm
plt.yscale('symlog', linthresh=1)
plt.grid(True)
plt.show()
Output:
在这个例子中,我们使用plt.yscale('symlog', linthresh=1)来创建一个对称的对数刻度。linthresh参数定义了线性区域的阈值。
7.2 使用LogNorm并添加一个小的常数
另一种处理零值和负值的方法是在数据中添加一个小的常数,然后使用常规的对数刻度。这种方法在某些情况下可能会引入偏差,但对于某些类型的数据可能是有用的。
import matplotlib.pyplot as plt
import numpy as np
# 生成包含零值的数据
x = np.linspace(0, 10, 100)
y = x**2 - 25
# 添加一个小的常数并取绝对值
y_shifted = np.abs(y + 1e-10)
# 创建图形
plt.figure(figsize=(10, 6))
plt.semilogy(x, y_shifted, label='Shifted Data')
plt.title('Log Scale with Shifted Data - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (log scale)')
plt.legend()
plt.grid(True)
plt.show()
Output:
在这个例子中,我们通过添加一个小的常数(1e-10)并取绝对值来处理零值和负值。这允许我们使用标准的对数刻度,但需要注意这种方法可能会影响数据的解释。
8. 自定义对数刻度的刻度线和标签
有时,默认的对数刻度刻度线和标签可能不满足我们的需求。Matplotlib允许我们自定义这些元素。
8.1 设置主刻度和次刻度
我们可以使用LogLocator来自定义主刻度和次刻度的位置:
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import LogLocator
# 生成数据
x = np.linspace(1, 1000, 1000)
y = x**2
# 创建图形
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, y)
ax.set_yscale('log')
ax.set_title('Custom Log Scale Ticks - how2matplotlib.com')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (log scale)')
# 设置主刻度和次刻度
ax.yaxis.set_major_locator(LogLocator(base=10, numticks=10))
ax.yaxis.set_minor_locator(LogLocator(base=10, subs=np.arange(2, 10) * 0.1, numticks=10))
ax.grid(True, which='both', ls='-', alpha=0.2)
plt.show()
Output:
在这个例子中,我们使用LogLocator来自定义主刻度和次刻度的位置。主刻度设置为10的幂,次刻度设置为主刻度之间的9个等分点。
8.2 自定义刻度标签
我们还可以自定义刻度标签的格式:
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import FuncFormatter
# 生成数据
x = np.linspace(1, 1000, 1000)
y = x**2
# 创建图形
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, y)
ax.set_yscale('log')
ax.set_title('Custom Log Scale Labels - how2matplotlib.com')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (log scale)')
# 自定义刻度标签格式
def log_tick_formatter(val, pos=None):
return f'10^{int(np.log10(val))}'
ax.yaxis.set_major_formatter(FuncFormatter(log_tick_formatter))
ax.grid(True)
plt.show()
Output:
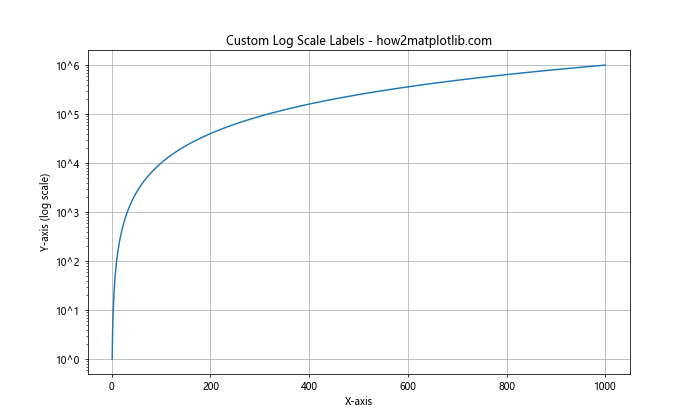
在这个例子中,我们定义了一个自定义函数log_tick_formatter来格式化刻度标签。这个函数将刻度值转换为10的幂的形式。
9. 在对数刻度中绘制误差线
在科学数据可视化中,我们经常需要绘制带有误差线的数据点。在对数刻度中绘制误差线需要特别注意,因为误差在对数空间中不是对称的。
以下是一个在对数刻度中绘制误差线的示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
x = np.array([1, 2, 3, 4, 5])
y = np.array([10, 100, 1000, 10000, 100000])
yerr = np.array([1, 10, 100, 1000, 10000])
# 创建图形
fig, ax = plt.subplots```python
fig, ax = plt.subplots(figsize=(10, 6))
# 绘制数据点和误差线
ax.errorbar(x, y, yerr=yerr, fmt='o', capsize=5, label='Data with Error')
ax.set_yscale('log')
ax.set_title('Error Bars in Log Scale - how2matplotlib.com')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis (log scale)')
ax.legend()
ax.grid(True)
plt.show()
在这个例子中,我们使用errorbar函数来绘制带有误差线的数据点。由于Y轴使用对数刻度,误差线在图中看起来是不对称的,这正确地反映了对数空间中误差的性质。
10. 对数-对数图(Log-Log Plot)
在某些情况下,我们可能需要同时将X轴和Y轴都设置为对数刻度,这就是所谓的对数-对数图(Log-Log Plot)。这种图形在分析幂律关系时特别有用。
以下是创建对数-对数图的示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
x = np.logspace(0, 3, 100)
y = x**2
# 创建对数-对数图
plt.figure(figsize=(10, 6))
plt.loglog(x, y, label='y = x^2')
plt.title('Log-Log Plot - how2matplotlib.com')
plt.xlabel('X-axis (log scale)')
plt.ylabel('Y-axis (log scale)')
plt.legend()
plt.grid(True, which="both", ls="-", alpha=0.2)
plt.show()
Output:
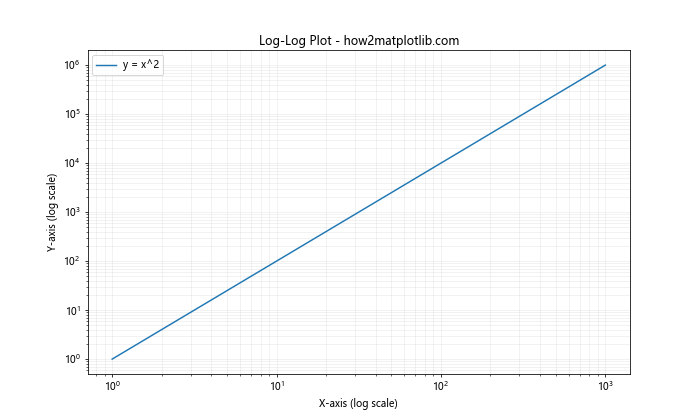
在这个例子中,我们使用plt.loglog()函数来创建一个对数-对数图。这个函数同时将X轴和Y轴设置为对数刻度。我们还使用np.logspace()函数来生成在对数空间中均匀分布的数据点。
11. 在对数刻度中绘制直方图
绘制对数刻度的直方图可以帮助我们更好地可视化跨越多个数量级的数据分布。以下是一个示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成对数正态分布的数据
data = np.random.lognormal(mean=1, sigma=1, size=10000)
# 创建直方图
plt.figure(figsize=(10, 6))
plt.hist(data, bins=50, range=(0, 100))
plt.title('Histogram with Log Scale Y-axis - how2matplotlib.com')
plt.xlabel('Value')
plt.ylabel('Frequency (log scale)')
# 设置Y轴为对数刻度
plt.yscale('log')
plt.grid(True, which="both", ls="-", alpha=0.2)
plt.show()
Output:
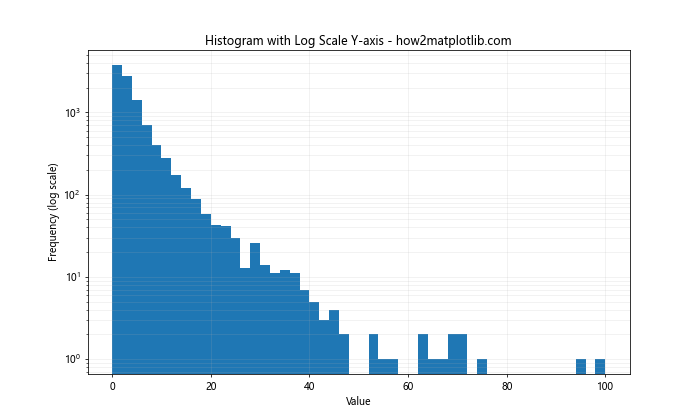
在这个例子中,我们生成了一个对数正态分布的数据集,并使用plt.hist()函数创建直方图。通过将Y轴设置为对数刻度,我们可以更清楚地看到数据分布的尾部。
12. 在对数刻度中绘制多个数据系列
当我们需要在同一个图中比较多个数据系列时,对数刻度可以帮助我们更好地展示它们之间的关系,特别是当这些系列的数值范围差异很大时。
以下是一个在对数刻度中绘制多个数据系列的示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
x = np.linspace(1, 10, 100)
y1 = x
y2 = x**2
y3 = x**3
y4 = 2**x
# 创建图形
plt.figure(figsize=(10, 6))
plt.semilogy(x, y1, label='Linear')
plt.semilogy(x, y2, label='Quadratic')
plt.semilogy(x, y3, label='Cubic')
plt.semilogy(x, y4, label='Exponential')
plt.title('Multiple Series in Log Scale - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (log scale)')
plt.legend()
plt.grid(True, which="both", ls="-", alpha=0.2)
plt.show()
Output:
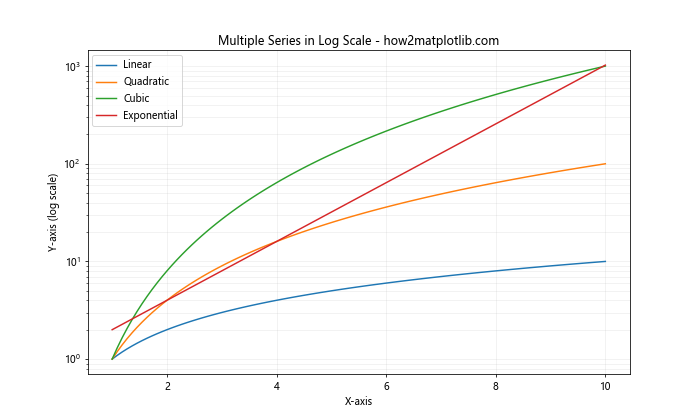
在这个例子中,我们绘制了四个不同的函数:线性、二次、三次和指数函数。通过使用对数刻度,我们可以在同一个图中清楚地看到这些函数的增长速度差异。
13. 在对数刻度中添加水平或垂直线
有时,我们可能需要在对数刻度图中添加水平或垂直线,例如,用于标记特定的阈值或参考值。以下是一个示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
x = np.linspace(1, 10, 100)
y = np.exp(x)
# 创建图形
plt.figure(figsize=(10, 6))
plt.semilogy(x, y, label='Exponential Growth')
# 添加水平线
plt.axhline(y=1000, color='r', linestyle='--', label='Threshold')
# 添加垂直线
plt.axvline(x=5, color='g', linestyle=':', label='Reference')
plt.title('Adding Lines in Log Scale - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (log scale)')
plt.legend()
plt.grid(True)
plt.show()
Output:
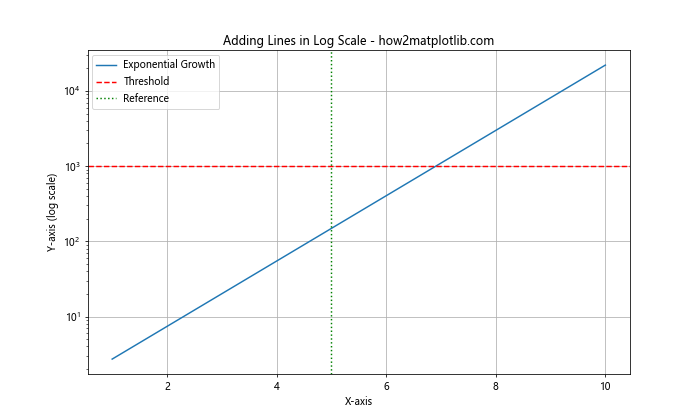
在这个例子中,我们使用plt.axhline()添加了一条水平线,用plt.axvline()添加了一条垂直线。这些线可以用来标记重要的阈值或参考点。
14. 在对数刻度中绘制填充区域
有时,我们可能想要在对数刻度图中突出显示某个区域。我们可以使用plt.fill_between()函数来实现这一点。以下是一个示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
x = np.linspace(1, 10, 100)
y1 = np.exp(x)
y2 = np.exp(x/2)
# 创建图形
plt.figure(figsize=(10, 6))
plt.semilogy(x, y1, label='Upper Bound')
plt.semilogy(x, y2, label='Lower Bound')
# 填充两条线之间的区域
plt.fill_between(x, y1, y2, alpha=0.3, label='Filled Area')
plt.title('Filled Area in Log Scale - how2matplotlib.com')
plt.xlabel('X-axis')
plt.ylabel('Y-axis (log scale)')
plt.legend()
plt.grid(True)
plt.show()
Output:
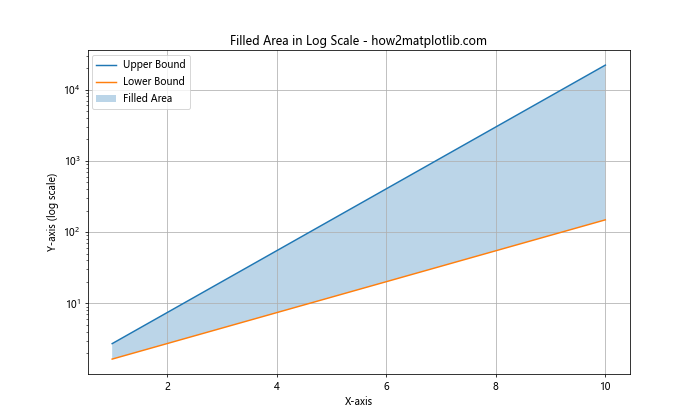
在这个例子中,我们绘制了两条曲线,并使用plt.fill_between()函数填充了它们之间的区域。这种技术在可视化置信区间或数据范围时特别有用。
15. 在对数刻度中使用双Y轴
有时,我们可能需要在同一个图中显示两个不同尺度的数据系列。我们可以使用双Y轴来实现这一点,其中一个轴可以是对数刻度,另一个是线性刻度。以下是一个示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成数据
x = np.linspace(1, 10, 100)
y1 = np.exp(x)
y2 = x**2
# 创建图形和主Y轴
fig, ax1 = plt.subplots(figsize=(10, 6))
# 绘制第一个数据系列(对数刻度)
color = 'tab:blue'
ax1.set_xlabel('X-axis')
ax1.set_ylabel('Y1 (log scale)', color=color)
ax1.semilogy(x, y1, color=color, label='Exponential')
ax1.tick_params(axis='y', labelcolor=color)
# 创建第二个Y轴
ax2 = ax1.twinx()
# 绘制第二个数据系列(线性刻度)
color = 'tab:orange'
ax2.set_ylabel('Y2 (linear scale)', color=color)
ax2.plot(x, y2, color=color, label='Quadratic')
ax2.tick_params(axis='y', labelcolor=color)
# 添加标题和图例
plt.title('Dual Y-axis with Log Scale - how2matplotlib.com')
fig.legend(loc="upper left", bbox_to_anchor=(0.1, 0.9))
plt.tight_layout()
plt.show()
Output:
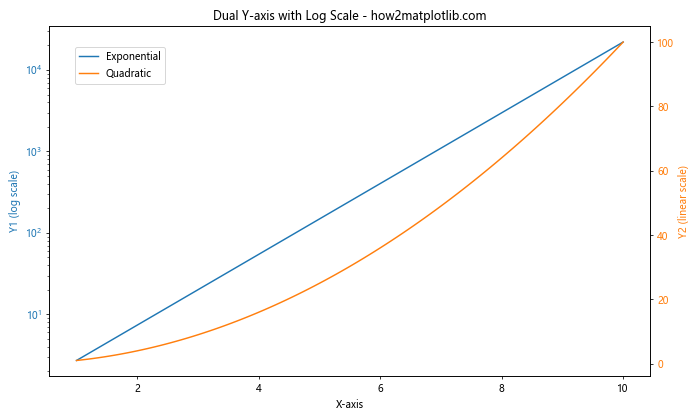
在这个例子中,我们创建了两个Y轴:左侧的Y轴使用对数刻度显示指数函数,右侧的Y轴使用线性刻度显示二次函数。这种方法允许我们在同一个图中比较不同尺度的数据。
结论
在本文中,我们详细探讨了如何在Matplotlib中将Y轴设置为对数刻度。我们介绍了基本方法,如使用plt.yscale('log')和plt.semilogy(),以及更高级的技巧,如自定义刻度和标签、处理负值和零值、绘制误差线和填充区域等。我们还讨论了对数-对数图和双Y轴图的创建方法。
对数刻度是数据可视化中的一个强大工具,特别是在处理跨越多个数量级的数据时。通过正确使用对数刻度,我们可以更有效地展示数据的模式和趋势,特别是在处理指数增长、幂律关系或高度倾斜的分布时。
然而,使用对数刻度时也需要注意一些潜在的陷阱。例如,对数刻度可能会误导不熟悉这种表示方法的观众,因为它压缩了大数值之间的差异。此外,处理包含零值或负值的数据时需要特别小心。
总的来说,掌握如何在Matplotlib中使用对数刻度将极大地增强你的数据可视化能力,使你能够更有效地传达复杂的数据关系和模式。
 极客笔记
极客笔记