如何在Python中创建残差图:全面指南与实例
参考:How to Create a Residual Plot in Python
残差图是数据分析和统计建模中的重要工具,它可以帮助我们评估模型的拟合程度和识别潜在的问题。本文将详细介绍如何在Python中使用Matplotlib库创建残差图,并提供多个实用示例。
1. 什么是残差图?
残差图是一种用于可视化回归模型预测值与实际观测值之间差异的图表。它可以帮助我们:
- 评估模型的拟合程度
- 检查模型假设是否成立
- 识别异常值和影响点
- 发现非线性关系
在残差图中,X轴通常表示预测值或自变量,Y轴表示残差(实际值减去预测值)。
2. 创建基本残差图
让我们从一个简单的示例开始,创建一个基本的残差图:
import numpy as np
import matplotlib.pyplot as plt
# 生成示例数据
np.random.seed(42)
x = np.linspace(0, 10, 100)
y = 2 * x + 1 + np.random.normal(0, 1, 100)
# 拟合线性模型
coeffs = np.polyfit(x, y, 1)
y_pred = np.polyval(coeffs, x)
# 计算残差
residuals = y - y_pred
# 创建残差图
plt.figure(figsize=(10, 6))
plt.scatter(y_pred, residuals, alpha=0.6)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot - how2matplotlib.com')
plt.show()
Output:
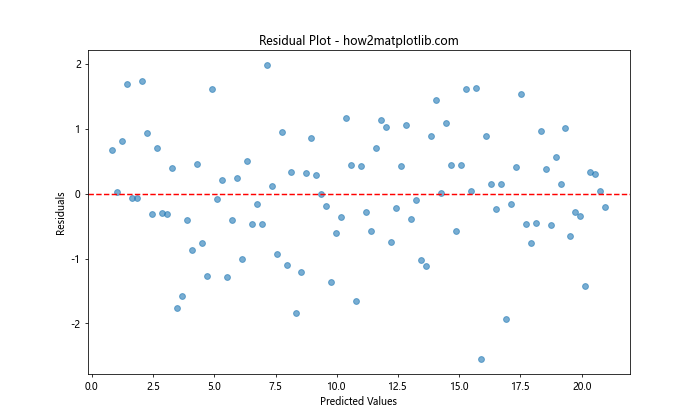
在这个示例中,我们首先生成了一些带有随机噪声的线性数据。然后,我们使用np.polyfit()拟合了一个线性模型,并计算了预测值和残差。最后,我们使用plt.scatter()创建了一个散点图,其中X轴是预测值,Y轴是残差。我们还添加了一条红色的水平虚线来表示y=0的位置,这有助于我们更好地观察残差的分布。
3. 添加额外的信息
为了使残差图更加信息丰富,我们可以添加一些额外的元素:
import numpy as np
import matplotlib.pyplot as plt
# 生成示例数据
np.random.seed(42)
x = np.linspace(0, 10, 100)
y = 2 * x + 1 + np.random.normal(0, 1, 100)
# 拟合线性模型
coeffs = np.polyfit(x, y, 1)
y_pred = np.polyval(coeffs, x)
# 计算残差
residuals = y - y_pred
# 创建残差图
plt.figure(figsize=(12, 8))
plt.scatter(y_pred, residuals, alpha=0.6, label='Residuals')
plt.axhline(y=0, color='r', linestyle='--', label='y=0')
# 添加趋势线
z = np.polyfit(y_pred, residuals, 1)
p = np.poly1d(z)
plt.plot(y_pred, p(y_pred), "r--", label='Trend')
# 添加均值和标准差
mean_residual = np.mean(residuals)
std_residual = np.std(residuals)
plt.axhline(y=mean_residual, color='g', linestyle='-', label=f'Mean ({mean_residual:.2f})')
plt.axhline(y=mean_residual + 2*std_residual, color='b', linestyle=':', label='+2 SD')
plt.axhline(y=mean_residual - 2*std_residual, color='b', linestyle=':', label='-2 SD')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Enhanced Residual Plot - how2matplotlib.com')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
Output:
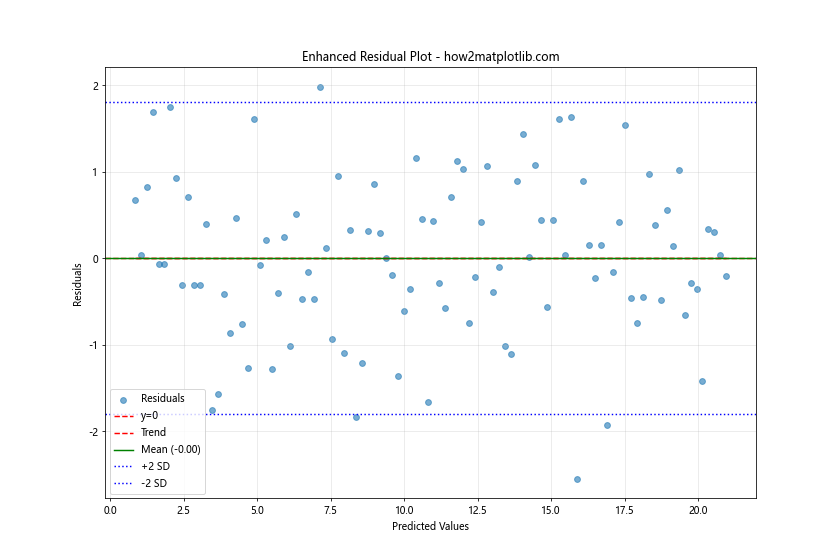
在这个增强版的残差图中,我们添加了以下元素:
- 残差的趋势线,帮助识别残差中的系统性模式
- 残差的平均值线
- 两个标准差的界限线,用于识别潜在的异常值
- 图例和网格线,提高可读性
这些额外的信息可以帮助我们更全面地理解模型的表现和残差的分布情况。
4. 创建分组残差图
在某些情况下,我们可能想要比较不同组或类别的残差分布。这时,我们可以创建分组残差图:
import numpy as np
import matplotlib.pyplot as plt
# 生成示例数据
np.random.seed(42)
x = np.linspace(0, 10, 100)
y1 = 2 * x + 1 + np.random.normal(0, 1, 100)
y2 = 1.5 * x + 2 + np.random.normal(0, 1.5, 100)
# 拟合线性模型
coeffs1 = np.polyfit(x, y1, 1)
coeffs2 = np.polyfit(x, y2, 1)
y_pred1 = np.polyval(coeffs1, x)
y_pred2 = np.polyval(coeffs2, x)
# 计算残差
residuals1 = y1 - y_pred1
residuals2 = y2 - y_pred2
# 创建分组残差图
plt.figure(figsize=(12, 8))
plt.scatter(y_pred1, residuals1, alpha=0.6, label='Group 1', color='blue')
plt.scatter(y_pred2, residuals2, alpha=0.6, label='Group 2', color='red')
plt.axhline(y=0, color='k', linestyle='--')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Grouped Residual Plot - how2matplotlib.com')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
Output:
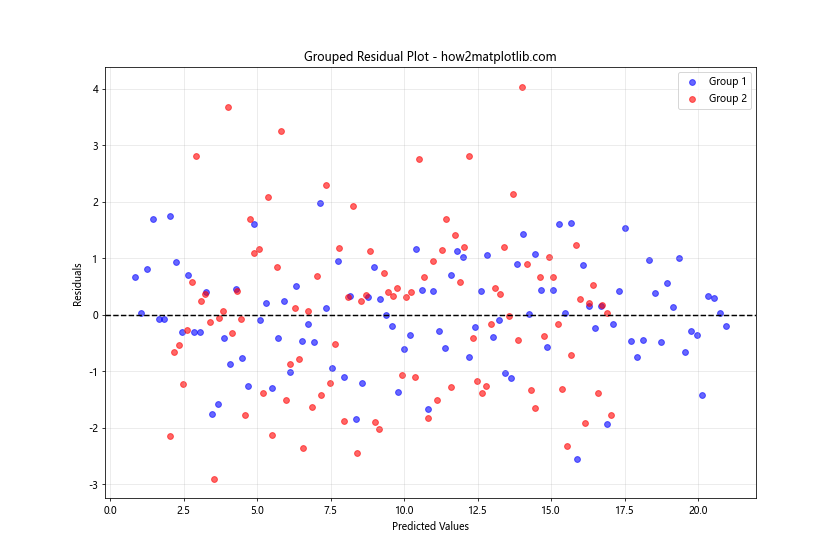
在这个示例中,我们生成了两组具有不同特征的数据,并为每组数据拟合了单独的线性模型。然后,我们在同一个图上绘制了两组数据的残差,使用不同的颜色进行区分。这种方法可以帮助我们比较不同组或模型之间的残差分布差异。
5. 创建残差直方图
除了散点图,我们还可以使用直方图来可视化残差的分布:
import numpy as np
import matplotlib.pyplot as plt
# 生成示例数据
np.random.seed(42)
x = np.linspace(0, 10, 1000)
y = 2 * x + 1 + np.random.normal(0, 1, 1000)
# 拟合线性模型
coeffs = np.polyfit(x, y, 1)
y_pred = np.polyval(coeffs, x)
# 计算残差
residuals = y - y_pred
# 创建残差直方图
plt.figure(figsize=(12, 8))
plt.hist(residuals, bins=30, edgecolor='black')
plt.axvline(x=0, color='r', linestyle='--', label='x=0')
plt.xlabel('Residuals')
plt.ylabel('Frequency')
plt.title('Residual Histogram - how2matplotlib.com')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
Output:
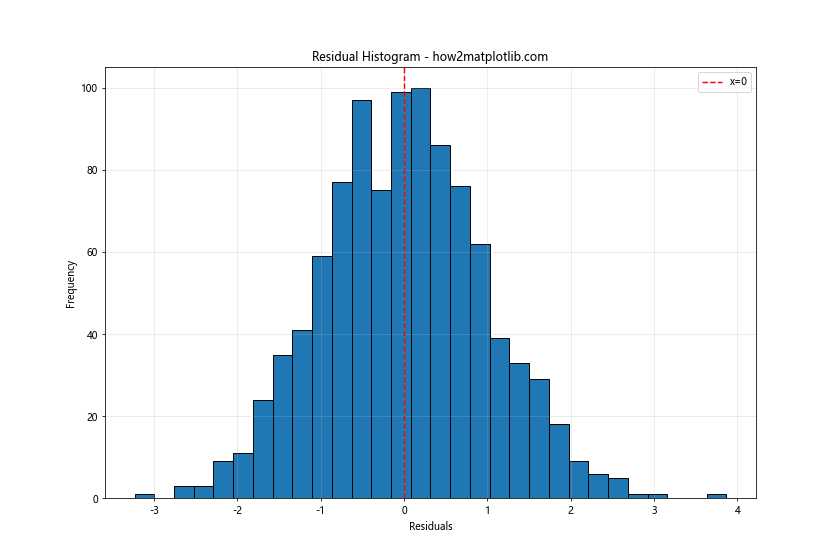
残差直方图可以帮助我们快速了解残差的分布情况,包括是否呈正态分布、是否存在偏斜或异常值等。在这个示例中,我们使用plt.hist()函数创建了一个直方图,并添加了一条垂直的红色虚线来表示x=0的位置。
6. 创建Q-Q图(Quantile-Quantile Plot)
Q-Q图是另一种用于评估残差分布的有用工具,特别是用于检查残差是否呈正态分布:
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 生成示例数据
np.random.seed(42)
x = np.linspace(0, 10, 1000)
y = 2 * x + 1 + np.random.normal(0, 1, 1000)
# 拟合线性模型
coeffs = np.polyfit(x, y, 1)
y_pred = np.polyval(coeffs, x)
# 计算残差
residuals = y - y_pred
# 创建Q-Q图
fig, ax = plt.subplots(figsize=(12, 8))
stats.probplot(residuals, dist="norm", plot=ax)
ax.set_title("Q-Q Plot of Residuals - how2matplotlib.com")
plt.show()
Output:
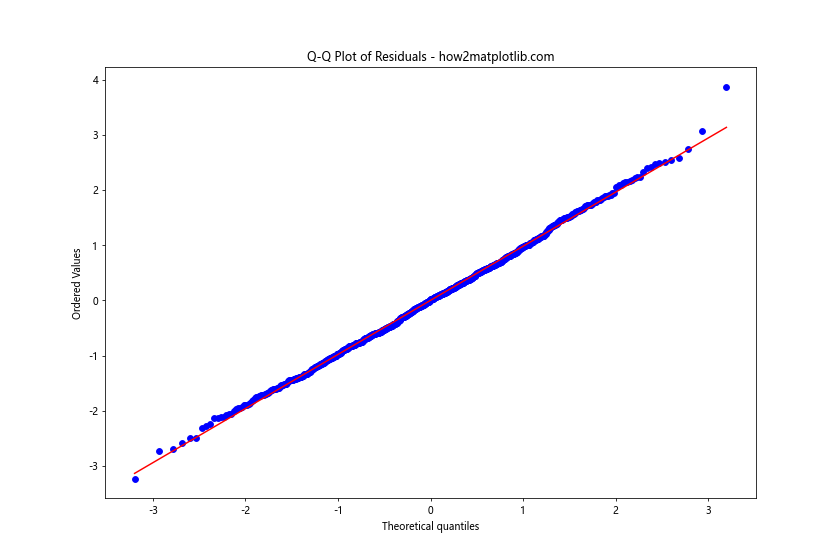
在这个示例中,我们使用了SciPy库的stats.probplot()函数来创建Q-Q图。如果残差呈正态分布,那么Q-Q图中的点应该大致落在一条直线上。任何显著的偏离都可能表明残差分布存在问题。
7. 创建残差箱线图
箱线图是另一种可以用来可视化残差分布的方法,特别适合比较多个组或类别的残差:
import numpy as np
import matplotlib.pyplot as plt
# 生成示例数据
np.random.seed(42)
x = np.linspace(0, 10, 1000)
y1 = 2 * x + 1 + np.random.normal(0, 1, 1000)
y2 = 1.5 * x + 2 + np.random.normal(0, 1.5, 1000)
y3 = 2.5 * x + 0.5 + np.random.normal(0, 0.8, 1000)
# 拟合线性模型
coeffs1 = np.polyfit(x, y1, 1)
coeffs2 = np.polyfit(x, y2, 1)
coeffs3 = np.polyfit(x, y3, 1)
y_pred1 = np.polyval(coeffs1, x)
y_pred2 = np.polyval(coeffs2, x)
y_pred3 = np.polyval(coeffs3, x)
# 计算残差
residuals1 = y1 - y_pred1
residuals2 = y2 - y_pred2
residuals3 = y3 - y_pred3
# 创建残差箱线图
plt.figure(figsize=(12, 8))
plt.boxplot([residuals1, residuals2, residuals3], labels=['Model 1', 'Model 2', 'Model 3'])
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Models')
plt.ylabel('Residuals')
plt.title('Residual Box Plot - how2matplotlib.com')
plt.grid(True, alpha=0.3)
plt.show()
Output:
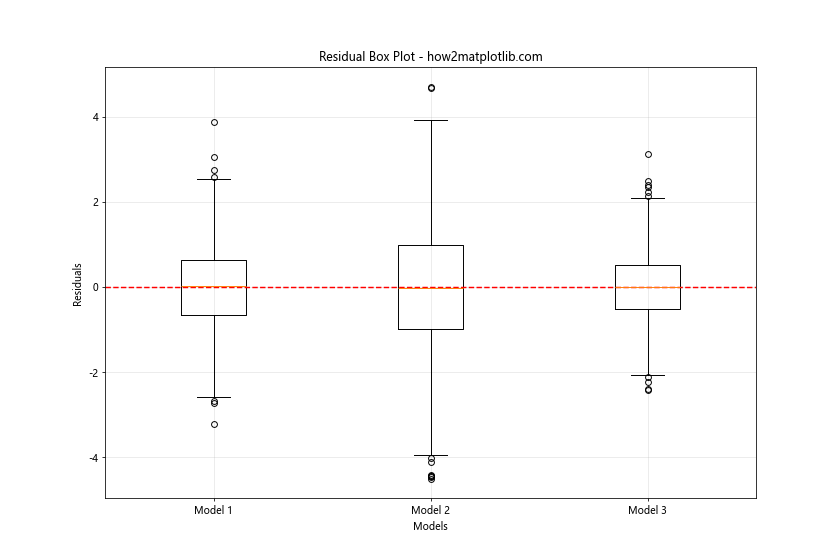
在这个示例中,我们为三个不同的模型创建了箱线图。箱线图可以显示残差的中位数、四分位数范围和潜在的异常值,使得比较不同模型或组的残差分布变得更加直观。
8. 创建残差热图
当我们有多个自变量时,可以使用热图来可视化残差与这些变量之间的关系:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成示例数据
np.random.seed(42)
X = np.random.rand(100, 3)
y = 2 * X[:, 0] + 3 * X[:, 1] - X[:, 2] + np.random.normal(0, 0.1, 100)
# 拟合线性模型
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)
# 计算残差
residuals = y - y_pred
# 创建残差热图
plt.figure(figsize=(12, 8))
plt.imshow([residuals], cmap='coolwarm', aspect='auto')
plt.colorbar(label='Residuals')
plt.yticks([])
plt.xticks(range(len(residuals)), range(1, len(residuals)+1), rotation=90)
plt.xlabel('Sample Index')
plt.title('Residual Heat Map - how2matplotlib.com')
plt.tight_layout()
plt.show()
Output:
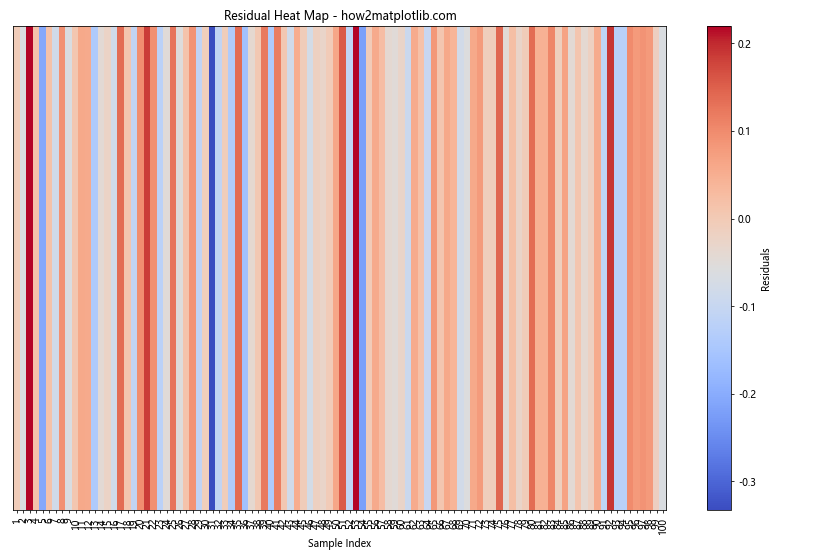
在这个示例中,我们使用了多元线性回归模型,并创建了一个残差热图。热图中的颜色表示残差的大小和方向,可以帮助我们识别残差中的模式或趋势。
9. 创建残差与预测值的关系图
为了更好地理解残差与预测值之间的关系,我们可以创建一个散点图,并添加一些额外的信息:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成示例数据
np.random.seed(42)
X = np.random.rand(100, 1)
y = 2 * X.ravel() + 1 + np.random.normal(0, 0.2, 100)
# 拟合线性模型
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)
# 计算残差
residuals = y - y_pred
# 创建残差与预测值的关系图
plt.figure(figsize=(12, 8))
plt.scatter(y_pred, residuals, alpha=0.6)
plt.axhline(y=0, color='r', linestyle='--')
# 添加趋势线
z = np.polyfit(y_pred, residuals, 1)
p = np.poly1d(z)
plt.plot(y_pred, p(y_pred), "g--", label='Trend')
# 添加置信区间
from scipy import stats
pred_interval = stats.t.intervalalpha = 0.95
df = len(X) - 2
pred_interval = stats.t.interval(alpha, df, loc=0, scale=np.std(residuals))
plt.fill_between(y_pred.ravel(), pred_interval[0], pred_interval[1], color='gray', alpha=0.2, label='95% Prediction Interval')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residuals vs Predicted Values - how2matplotlib.com')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
在这个示例中,我们创建了一个残差与预测值的关系图。我们添加了一条趋势线来显示残差与预测值之间的整体关系,还添加了一个95%的预测区间。这种图可以帮助我们识别残差中的任何系统性模式或异方差性。
10. 创建残差的时间序列图
如果我们的数据具有时间顺序,创建残差的时间序列图可能会很有用:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成示例时间序列数据
np.random.seed(42)
time = np.arange(100)
y = 0.5 * time + 10 + np.random.normal(0, 5, 100)
# 拟合线性模型
model = LinearRegression()
model.fit(time.reshape(-1, 1), y)
y_pred = model.predict(time.reshape(-1, 1))
# 计算残差
residuals = y - y_pred
# 创建残差的时间序列图
plt.figure(figsize=(12, 8))
plt.plot(time, residuals, marker='o', linestyle='-', markersize=4, alpha=0.6)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Time')
plt.ylabel('Residuals')
plt.title('Residual Time Series Plot - how2matplotlib.com')
plt.grid(True, alpha=0.3)
plt.show()
Output:
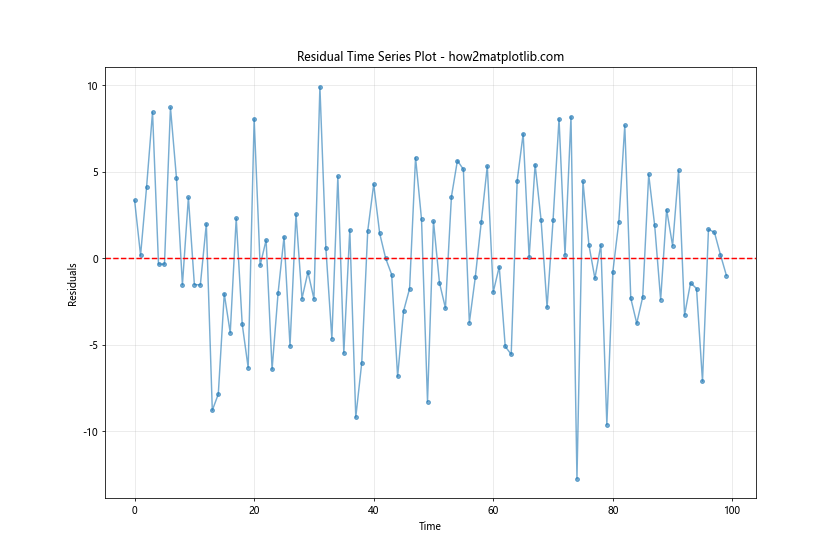
这个时间序列残差图可以帮助我们识别残差中的时间相关模式,如趋势、季节性或自相关。
11. 创建残差的自相关图
为了进一步检查残差中的时间相关性,我们可以创建一个自相关图:
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
# 生成示例时间序列数据
np.random.seed(42)
time = np.arange(100)
y = 0.5 * time + 10 + np.sin(time/10) + np.random.normal(0, 2, 100)
# 拟合线性模型
coeffs = np.polyfit(time, y, 1)
y_pred = np.polyval(coeffs, time)
# 计算残差
residuals = y - y_pred
# 创建残差的自相关图
plt.figure(figsize=(12, 8))
plot_acf(residuals, lags=20, alpha=0.05, title="Residual Autocorrelation Plot - how2matplotlib.com")
plt.show()
Output:
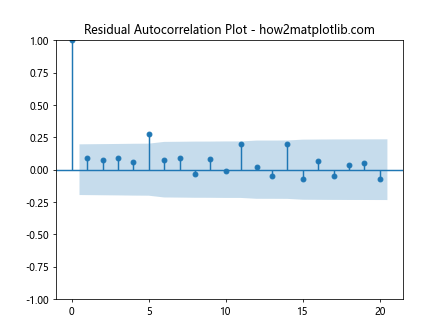
自相关图可以帮助我们识别残差中的序列相关性。如果残差是随机的,大多数滞后的自相关应该在置信区间内。
12. 创建残差的部分自相关图
部分自相关图是自相关图的补充,可以帮助我们识别时间序列中的直接依赖关系:
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_pacf
# 生成示例时间序列数据
np.random.seed(42)
time = np.arange(100)
y = 0.5 * time + 10 + np.sin(time/10) + np.random.normal(0, 2, 100)
# 拟合线性模型
coeffs = np.polyfit(time, y, 1)
y_pred = np.polyval(coeffs, time)
# 计算残差
residuals = y - y_pred
# 创建残差的部分自相关图
plt.figure(figsize=(12, 8))
plot_pacf(residuals, lags=20, alpha=0.05, title="Residual Partial Autocorrelation Plot - how2matplotlib.com")
plt.show()
Output:
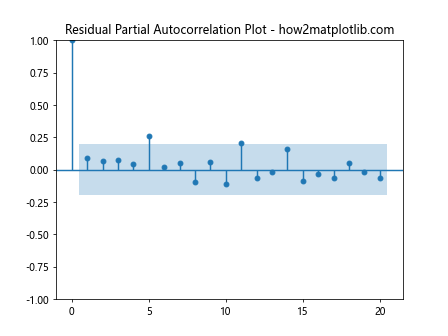
部分自相关图可以帮助我们确定时间序列模型的适当阶数,特别是在ARIMA模型中。
13. 创建残差的核密度估计图
核密度估计图是另一种可视化残差分布的方法,它可以提供比直方图更平滑的分布估计:
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 生成示例数据
np.random.seed(42)
x = np.linspace(0, 10, 1000)
y = 2 * x + 1 + np.random.normal(0, 1, 1000)
# 拟合线性模型
coeffs = np.polyfit(x, y, 1)
y_pred = np.polyval(coeffs, x)
# 计算残差
residuals = y - y_pred
# 创建残差的核密度估计图
plt.figure(figsize=(12, 8))
residuals_kde = stats.gaussian_kde(residuals)
x_range = np.linspace(residuals.min(), residuals.max(), 100)
plt.plot(x_range, residuals_kde(x_range))
plt.hist(residuals, bins=30, density=True, alpha=0.5)
plt.axvline(x=0, color='r', linestyle='--')
plt.xlabel('Residuals')
plt.ylabel('Density')
plt.title('Residual Kernel Density Estimation - how2matplotlib.com')
plt.grid(True, alpha=0.3)
plt.show()
Output:
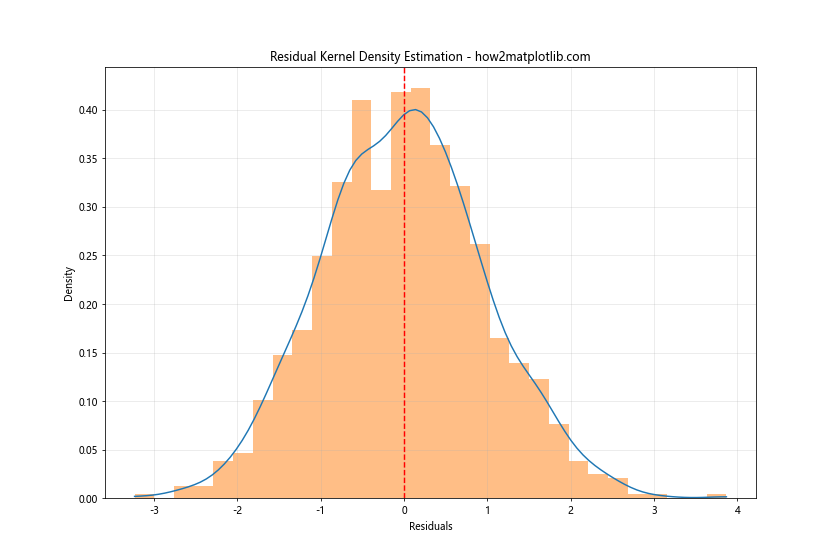
这个图结合了核密度估计和直方图,可以帮助我们更好地理解残差的分布情况。
14. 创建残差的3D散点图
当我们有多个自变量时,可以创建一个3D散点图来可视化残差与两个主要自变量之间的关系:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import LinearRegression
# 生成示例数据
np.random.seed(42)
X = np.random.rand(100, 2)
y = 2 * X[:, 0] + 3 * X[:, 1] + np.random.normal(0, 0.1, 100)
# 拟合线性模型
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)
# 计算残差
residuals = y - y_pred
# 创建残差的3D散点图
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
scatter = ax.scatter(X[:, 0], X[:, 1], residuals, c=residuals, cmap='coolwarm')
plt.colorbar(scatter)
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.set_zlabel('Residuals')
ax.set_title('3D Residual Plot - how2matplotlib.com')
plt.show()
Output:
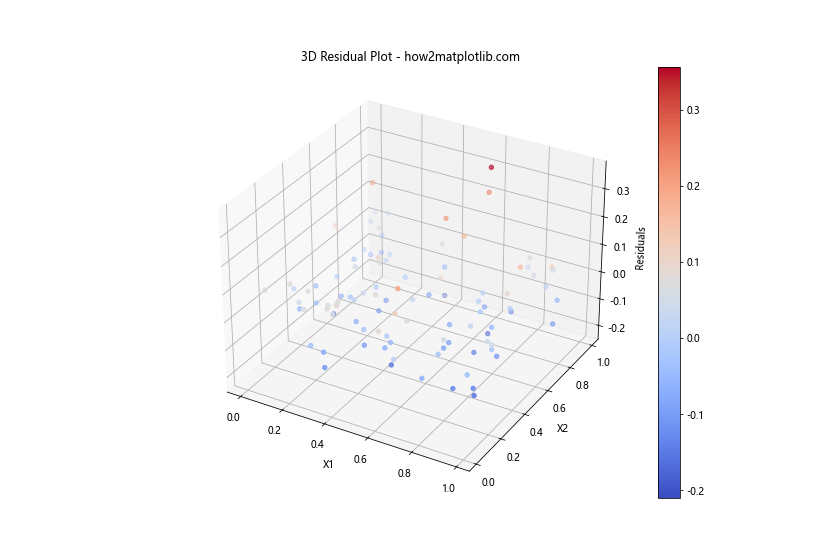
这个3D散点图可以帮助我们识别残差与两个主要自变量之间的复杂关系。
15. 创建残差的等高线图
等高线图是另一种可视化多变量关系的方法,特别适合展示残差与两个自变量之间的关系:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成示例数据
np.random.seed(42)
X = np.random.rand(1000, 2)
y = 2 * X[:, 0] + 3 * X[:, 1] + np.random.normal(0, 0.1, 1000)
# 拟合线性模型
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)
# 计算残差
residuals = y - y_pred
# 创建残差的等高线图
plt.figure(figsize=(12, 8))
contour = plt.tricontourf(X[:, 0], X[:, 1], residuals, cmap='coolwarm', levels=20)
plt.colorbar(contour)
plt.scatter(X[:, 0], X[:, 1], c=residuals, cmap='coolwarm', alpha=0.5, s=10)
plt.xlabel('X1')
plt.ylabel('X2')
plt.title('Residual Contour Plot - how2matplotlib.com')
plt.show()
Output:
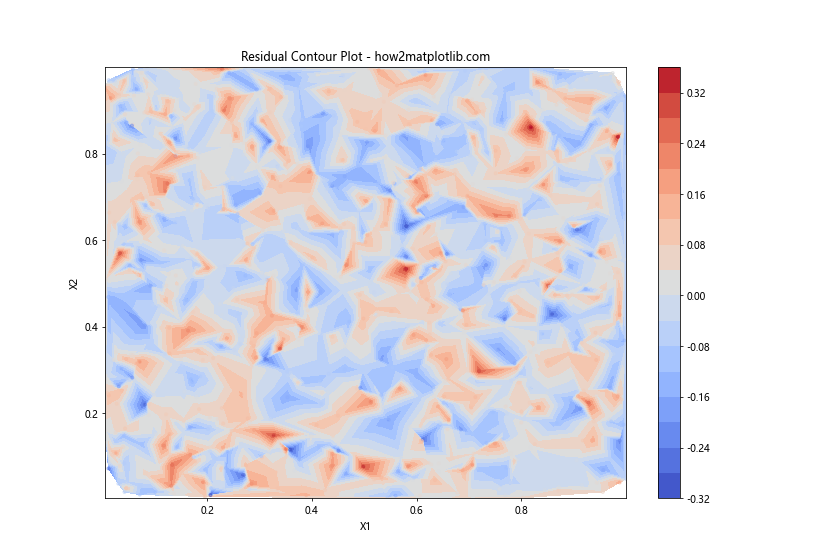
这个等高线图结合了散点图,可以帮助我们识别残差在两个自变量空间中的分布模式。
结论
在本文中,我们详细探讨了如何在Python中使用Matplotlib创建各种类型的残差图。从基本的散点图到高级的3D和等高线图,这些可视化技术为我们提供了强大的工具来评估模型性能、检查模型假设,并识别潜在的问题。
通过结合使用这些不同类型的残差图,我们可以全面地分析模型的残差,从而做出更加明智的决策,改进我们的统计模型。记住,没有一种单一的图表能够告诉我们关于残差的所有信息,因此综合使用多种可视化技术通常是最佳的做法。
在实际应用中,选择合适的残差图类型取决于你的具体问题、数据特征和分析目标。希望这篇文章能够为你提供一个全面的工具箱,帮助你更好地理解和可视化模型残差。
 极客笔记
极客笔记