当前位置：极客笔记 > Matplotlib > Matplotlib 问答 > Matplotlib直方图中的箱宽设置：全面指南与实践

Matplotlib直方图中的箱宽设置：全面指南与实践

Matplotlib直方图中的箱宽设置：全面指南与实践

参考：Bin Size in Matplotlib Histogram

直方图是数据可视化中常用的一种图表类型，它能够直观地展示数据的分布情况。在使用Matplotlib绘制直方图时，箱宽（Bin Size）的设置是一个关键参数，它直接影响着直方图的外观和数据解释。本文将深入探讨Matplotlib直方图中箱宽的概念、设置方法以及其对数据展示的影响，并通过多个实例来展示如何灵活运用箱宽设置来优化直方图的表现。

1. 直方图箱宽的基本概念

在开始深入探讨之前，我们首先需要理解什么是直方图的箱宽。箱宽是指直方图中每个柱子所代表的数据范围。例如，如果我们有一组从0到100的数据，并将箱宽设置为10，那么直方图将会有10个柱子，分别代表0-10、10-20、20-30等范围内的数据频次。

箱宽的选择对直方图的呈现效果有着重要影响：
– 箱宽过大可能会掩盖数据的细节特征
– 箱宽过小则可能会使图形变得杂乱，难以辨识整体趋势

因此，选择合适的箱宽是绘制直方图时的一个关键考虑因素。

让我们通过一个简单的例子来看看箱宽是如何影响直方图的：

import matplotlib.pyplot as plt
import numpy as np

# 生成随机数据
np.random.seed(42)
data = np.random.normal(loc=0, scale=1, size=1000)

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制直方图，设置箱宽为0.5
plt.hist(data, bins=np.arange(min(data), max(data) + 0.5, 0.5), edgecolor='black')

# 设置标题和标签
plt.title('Histogram with Bin Size 0.5 - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

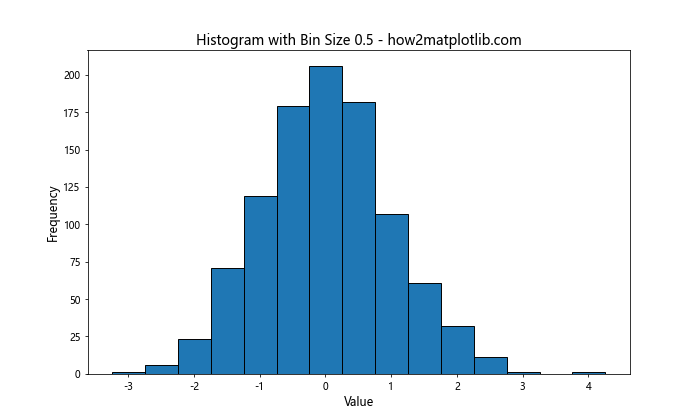
在这个例子中，我们生成了1000个服从标准正态分布的随机数，并使用plt.hist()函数绘制直方图。通过设置bins参数，我们指定了箱宽为0.5。这个设置使得直方图能够较为清晰地展示数据的分布特征，既不会过于粗糙，也不会过于细碎。

2. Matplotlib中设置箱宽的方法

Matplotlib提供了多种方法来设置直方图的箱宽。我们可以通过bins参数来控制箱子的数量或宽度。以下是几种常见的设置方式：

2.1 指定箱子的数量

最简单的方法是直接指定想要的箱子数量：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
np.random.seed(42)
data = np.random.exponential(scale=2, size=1000)

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制直方图，指定30个箱子
plt.hist(data, bins=30, edgecolor='black')

# 设置标题和标签
plt.title('Histogram with 30 Bins - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

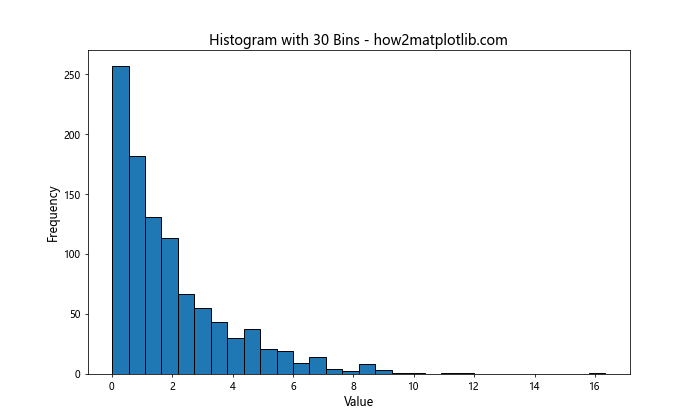
在这个例子中，我们通过设置bins=30来指定直方图应该有30个箱子。Matplotlib会自动计算每个箱子的宽度，以覆盖整个数据范围。

2.2 指定箱宽

如果我们想要更精确地控制箱宽，可以直接指定箱子的边界：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
np.random.seed(42)
data = np.random.normal(loc=5, scale=2, size=1000)

# 创建图形
plt.figure(figsize=(10, 6))

# 指定箱子边界，箱宽为1
bins = np.arange(min(data), max(data) + 1, 1)

# 绘制直方图
plt.hist(data, bins=bins, edgecolor='black')

# 设置标题和标签
plt.title('Histogram with Bin Width 1 - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

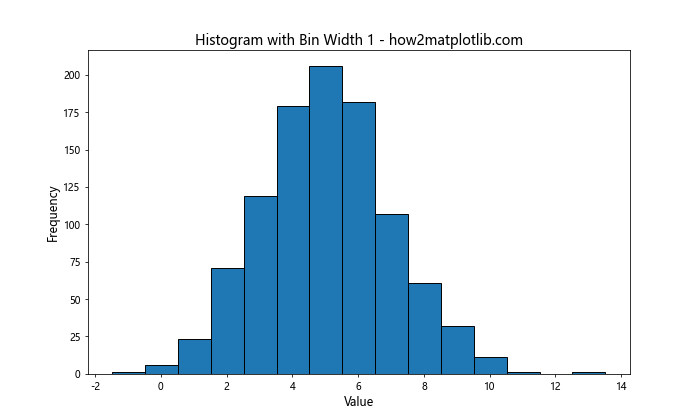
在这个例子中，我们使用np.arange()函数创建了一个等间隔的数组作为箱子的边界。这样可以精确控制每个箱子的宽度为1。

2.3 使用字符串参数

Matplotlib还提供了一些预定义的字符串参数来自动选择箱宽：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
np.random.seed(42)
data = np.random.gamma(shape=2, scale=2, size=1000)

# 创建图形
plt.figure(figsize=(10, 6))

# 使用'auto'参数自动选择箱宽
plt.hist(data, bins='auto', edgecolor='black')

# 设置标题和标签
plt.title("Histogram with 'auto' Bins - how2matplotlib.com", fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

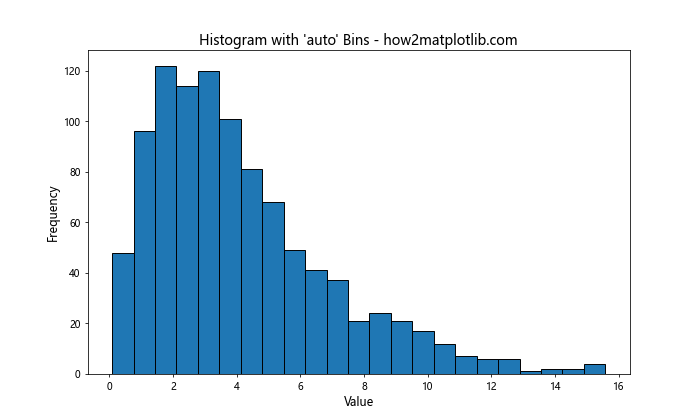
在这个例子中，我们使用bins='auto'让Matplotlib自动选择合适的箱宽。其他可用的字符串参数包括’fd’（Freedman-Diaconis规则）、’sturges’（Sturges规则）和’scott’（Scott规则）等。

3. 箱宽对数据解释的影响

箱宽的选择不仅影响直方图的视觉效果，还会影响我们对数据的解释。让我们通过一个例子来看看不同的箱宽如何影响同一组数据的呈现：

import matplotlib.pyplot as plt
import numpy as np

# 生成双峰数据
np.random.seed(42)
data = np.concatenate([np.random.normal(0, 1, 1000), np.random.normal(4, 1, 1000)])

# 创建一个2x2的子图
fig, axs = plt.subplots(2, 2, figsize=(12, 10))

# 不同的箱宽设置
bin_settings = [10, 30, 50, 100]

for ax, bins in zip(axs.ravel(), bin_settings):
    ax.hist(data, bins=bins, edgecolor='black')
    ax.set_title(f'Bins: {bins} - how2matplotlib.com', fontsize=12)
    ax.set_xlabel('Value', fontsize=10)
    ax.set_ylabel('Frequency', fontsize=10)

plt.tight_layout()
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

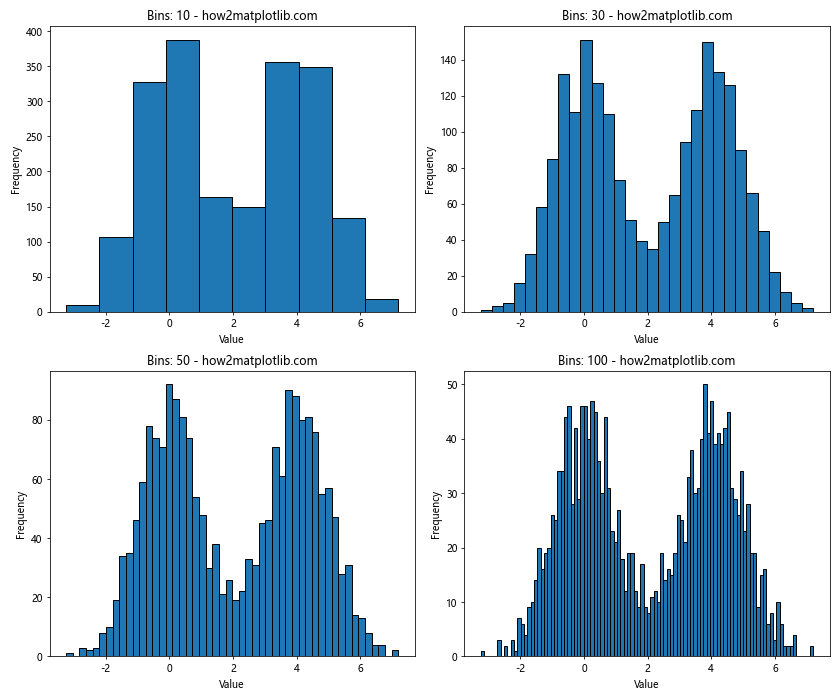
在这个例子中，我们生成了一个双峰分布的数据集，并使用不同的箱数（10、30、50和100）来绘制直方图。通过比较这些图，我们可以看到：

  • 当箱数较少（10个）时，直方图无法清晰地显示数据的双峰特性。
  • 随着箱数的增加，双峰特性逐渐变得明显。
  • 当箱数过多（100个）时，图形变得杂乱，难以辨识整体趋势。

这个例子说明了选择适当的箱宽对于正确解释数据分布的重要性。

4. 高级箱宽设置技巧

除了基本的箱宽设置方法，Matplotlib还提供了一些高级技巧来优化直方图的表现。

4.1 不等宽箱子

在某些情况下，使用等宽的箱子可能无法很好地展示数据的特征。Matplotlib允许我们使用不等宽的箱子：

import matplotlib.pyplot as plt
import numpy as np

# 生成对数正态分布的数据
np.random.seed(42)
data = np.random.lognormal(mean=0, sigma=1, size=1000)

# 创建图形
plt.figure(figsize=(10, 6))

# 使用对数刻度的箱子
bins = np.logspace(np.log10(data.min()), np.log10(data.max()), 30)

# 绘制直方图
plt.hist(data, bins=bins, edgecolor='black')
plt.xscale('log')

# 设置标题和标签
plt.title('Histogram with Logarithmic Bins - how2matplotlib.com', fontsize=14)
plt.xlabel('Value (log scale)', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

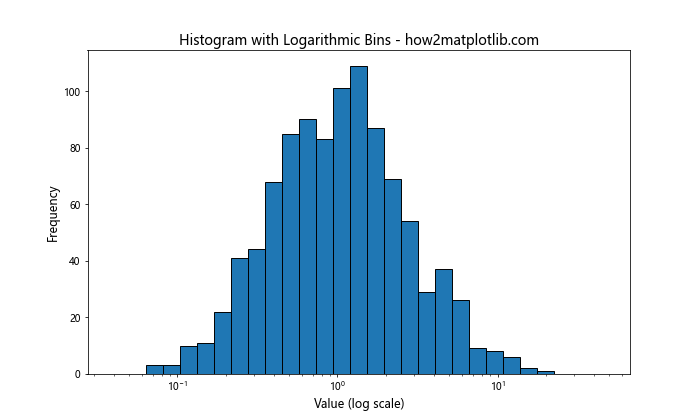
在这个例子中，我们使用np.logspace()创建了一个对数刻度的箱子序列。这种方法特别适合处理跨越多个数量级的数据。

4.2 多数据集比较

当我们需要比较多个数据集时，可以使用重叠的直方图：

import matplotlib.pyplot as plt
import numpy as np

# 生成两组数据
np.random.seed(42)
data1 = np.random.normal(0, 1, 1000)
data2 = np.random.normal(2, 1.5, 1000)

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制重叠的直方图
plt.hist(data1, bins=30, alpha=0.7, label='Dataset 1')
plt.hist(data2, bins=30, alpha=0.7, label='Dataset 2')

# 设置标题和标签
plt.title('Overlapping Histograms - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)
plt.legend()

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

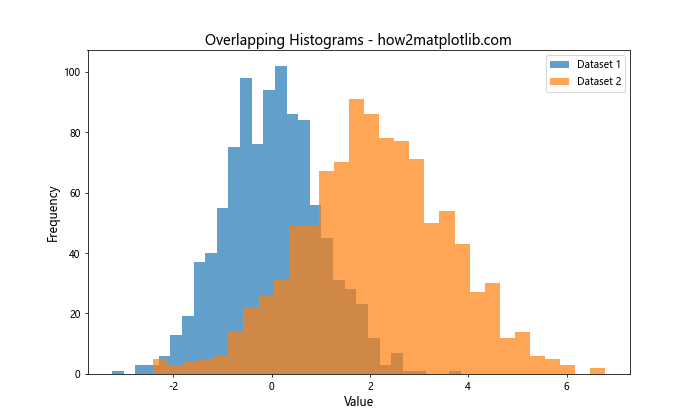
在这个例子中，我们使用alpha参数来设置直方图的透明度，使两个数据集的分布可以同时可见。

4.3 累积直方图

累积直方图可以帮助我们理解数据的累积分布：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
np.random.seed(42)
data = np.random.exponential(scale=2, size=1000)

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制累积直方图
plt.hist(data, bins=30, cumulative=True, edgecolor='black')

# 设置标题和标签
plt.title('Cumulative Histogram - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Cumulative Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

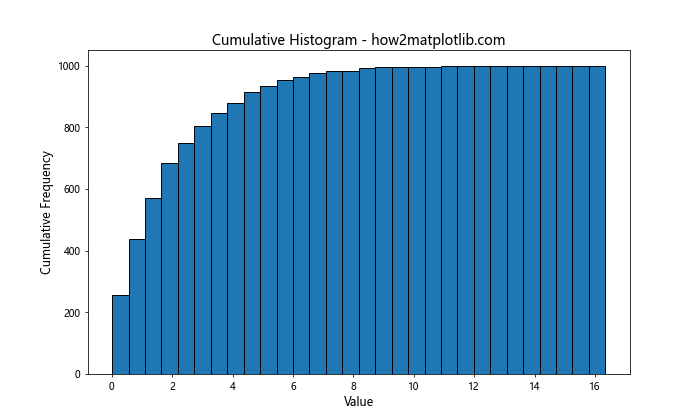
通过设置cumulative=True，我们可以绘制累积直方图，这对于理解数据的分位数和百分比分布非常有用。

5. 箱宽的自动选择算法

Matplotlib提供了几种自动选择箱宽的算法。这些算法试图在数据表示的精确性和图形的可读性之间找到平衡。让我们来看看几种常用的算法：

5.1 Sturges规则

Sturges规则是一种简单的方法，它基于数据点的数量来确定箱子的数量：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
np.random.seed(42)
data = np.random.normal(loc=0, scale=1, size=1000)

# 创建图形
plt.figure(figsize=(10, 6))

# 使用Sturges规则
plt.hist(data, bins='sturges', edgecolor='black')

# 设置标题和标签
plt.title("Histogram with Sturges' Rule - how2matplotlib.com", fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

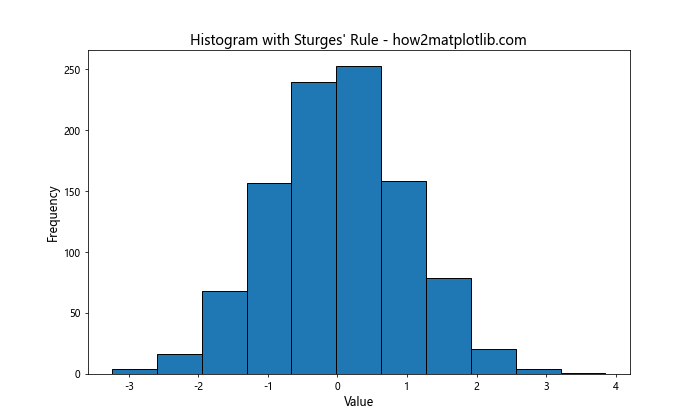
Sturges规则计算箱子数量的公式为：1 + log2(n)，其中n是数据点的数量。这种方法在数据近似正态分布时效果较好，但对于偏斜分布可能不太适用。

5.2 Freedman-Diaconis规则

Freedman-Diaconis规则考虑了数据的分布特征，特别是四分位距：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
np.random.seed(42)
data = np.random.gamma(shape=2, scale=2, size=1000)

# 创建图形
plt.figure(figsize=(10, 6))

# 使用Freedman-Diaconis规则
plt.hist(data, bins='fd', edgecolor='black')

# 设置标题和标签
plt.title("Histogram with Freedman-Diaconis Rule - how2matplotlib.com", fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

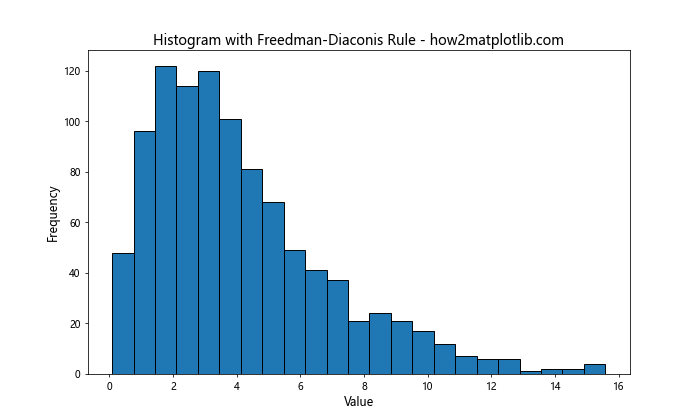
Freedman-Diaconis规则计算箱宽的公式为：2 * IQR * n^(-1/3)，其中IQR是四分位距，n是数据点的数量。这种方法对异常值不太敏感，适用于各种分布类型。

5.3 Scott规则

Scott规则是另一种常用的自动箱宽选择方法：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
np.random.seed(42)
data = np.random.beta(a=2, b=5, size=1000)

# 创建图形
plt.figure(figsize=(10, 6))

# 使用Scott规则
plt.hist(data, bins='scott', edgecolor='black')

# 设置标题和标签
plt.title("Histogram with Scott's Rule - how2matplotlib.com", fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

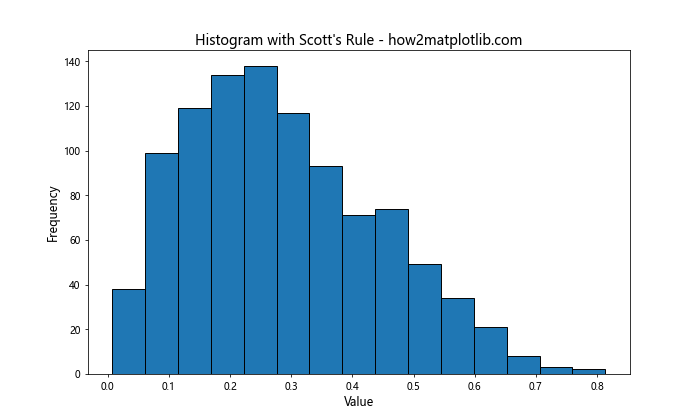
Scott规则计算箱宽的公式为：3.5 * σ * n^(-1/3)，其中σ是数据的标准差，n是数据点的数量。这种方法假设数据近似正态分布，并且对异常值比较敏感。

6. 箱宽对不同类型数据的影响

不同类型的数据分布可能需要不同的箱宽设置策略。让我们探讨一下箱宽对几种常见数据类型的影响：

6.1 正态分布数据

对于正态分布的数据，中等数量的箱子通常能很好地展示分布特征：

import matplotlib.pyplot as plt
import numpy as np

# 生成正态分布数据
np.random.seed(42)
data = np.random.normal(loc=0, scale=1, size=10000)

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制直方图
plt.hist(data, bins=50, edgecolor='black')

# 设置标题和标签
plt.title('Histogram of Normal Distribution - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

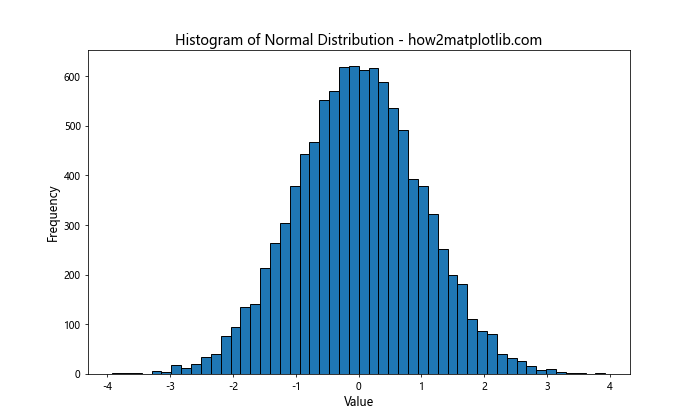
对于正态分布，50个箱子通常能够很好地展示钟形曲线的特征。

6.2 偏斜分布数据

对于偏斜分布，可能需要更多的箱子来捕捉分布的细节：

import matplotlib.pyplot as plt
import numpy as np

# 生成偏斜分布数据
np.random.seed(42)
data = np.random.lognormal(mean=0, sigma=0.5, size=10000)

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制直方图
plt.hist(data, bins=100, edgecolor='black')

# 设置标题和标签
plt.title('Histogram of Skewed Distribution - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

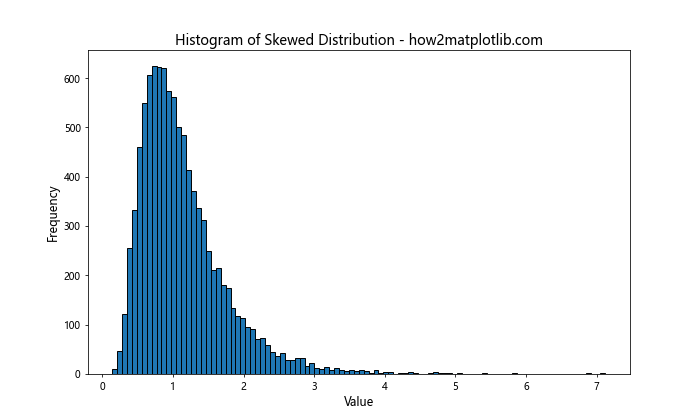
对于这种右偏的对数正态分布，使用更多的箱子（如100个）可以更好地展示分布的长尾特征。

6.3 多峰分布数据

对于多峰分布，箱宽的选择尤为重要，因为它可能影响我们对峰值数量的判断：

import matplotlib.pyplot as plt
import numpy as np

# 生成多峰分布数据
np.random.seed(42)
data = np.concatenate([
    np.random.normal(-3, 1, 3000),
    np.random.normal(0, 1, 4000),
    np.random.normal(3, 1, 3000)
])

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制直方图
plt.hist(data, bins=80, edgecolor='black')

# 设置标题和标签
plt.title('Histogram of Multimodal Distribution - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

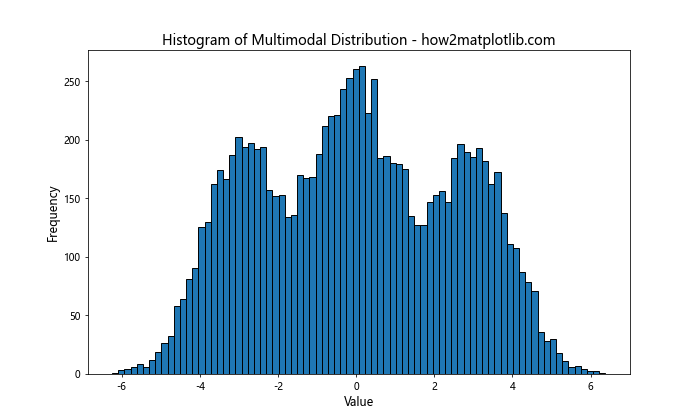
对于这种三峰分布，使用80个箱子可以清晰地展示出三个峰值。如果箱子太少，可能会掩盖某些峰值；如果太多，则可能引入不必要的噪声。

7. 箱宽与样本大小的关系

样本大小也是影响箱宽选择的一个重要因素。一般来说，样本越大，我们可以使用更多的箱子来展示更细致的分布特征。

7.1 小样本

对于小样本，使用较少的箱子可以避免过度拟合：

import matplotlib.pyplot as plt
import numpy as np

# 生成小样本数据
np.random.seed(42)
small_sample = np.random.normal(loc=0, scale=1, size=50)

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制直方图
plt.hist(small_sample, bins=10, edgecolor='black')

# 设置标题和标签
plt.title('Histogram of Small Sample - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

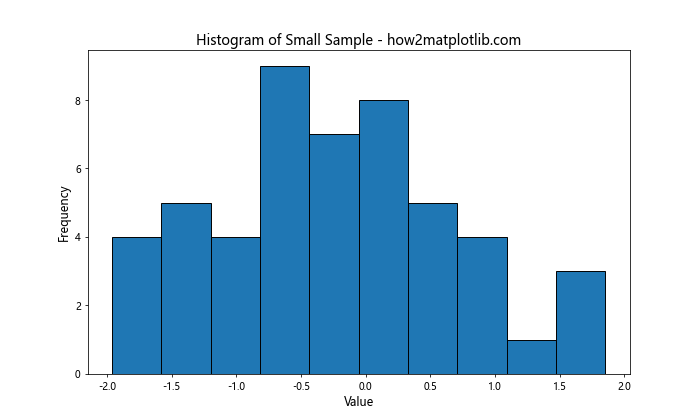
对于只有50个数据点的小样本，使用10个箱子可以给出一个合理的分布概览，而不会引入太多噪声。

7.2 大样本

对于大样本，我们可以使用更多的箱子来展示更多细节：

import matplotlib.pyplot as plt
import numpy as np

# 生成大样本数据
np.random.seed(42)
large_sample = np.random.normal(loc=0, scale=1, size=100000)

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制直方图
plt.hist(large_sample, bins=200, edgecolor='black')

# 设置标题和标签
plt.title('Histogram of Large Sample - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

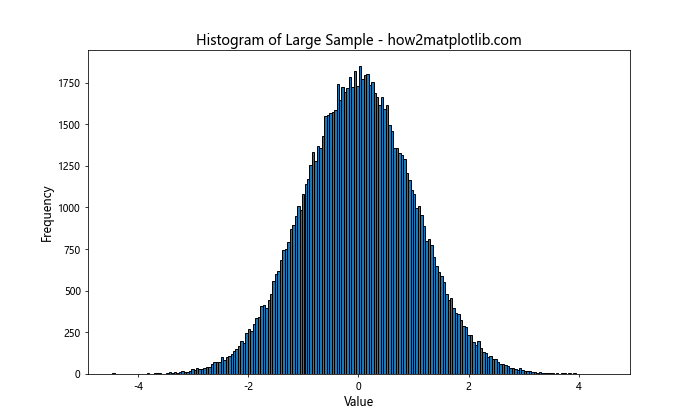
对于10万个数据点的大样本，使用200个箱子可以展示出更细致的分布特征，而不会使图形变得过于杂乱。

8. 箱宽与可视化目标的关系

选择合适的箱宽还需要考虑我们的可视化目标。不同的目标可能需要不同的箱宽设置。

8.1 展示整体趋势

如果目标是展示数据的整体趋势，可以使用较少的箱子：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据
np.random.seed(42)
data = np.random.gamma(shape=2, scale=2, size=10000)

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制直方图
plt.hist(data, bins=30, edgecolor='black')

# 设置标题和标签
plt.title('Overall Trend Visualization - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

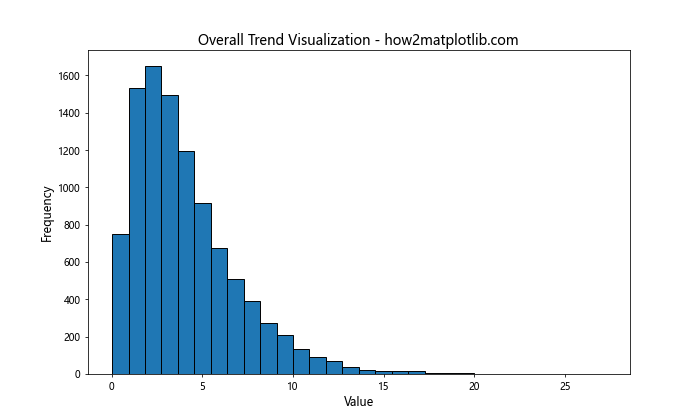
使用30个箱子可以清晰地展示数据的整体分布趋势，而不会被细节干扰。

8.2 突出异常值

如果目标是检测异常值，可能需要使用更多的箱子：

import matplotlib.pyplot as plt
import numpy as np

# 生成数据，包括一些异常值
np.random.seed(42)
data = np.concatenate([
    np.random.normal(loc=0, scale=1, size=9900),
    np.random.uniform(low=5, high=10, size=100)  # 异常值
])

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制直方图
plt.hist(data, bins=100, edgecolor='black')

# 设置标题和标签
plt.title('Anomaly Detection Visualization - how2matplotlib.com', fontsize=14)
plt.xlabel('Value', fontsize=12)
plt.ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

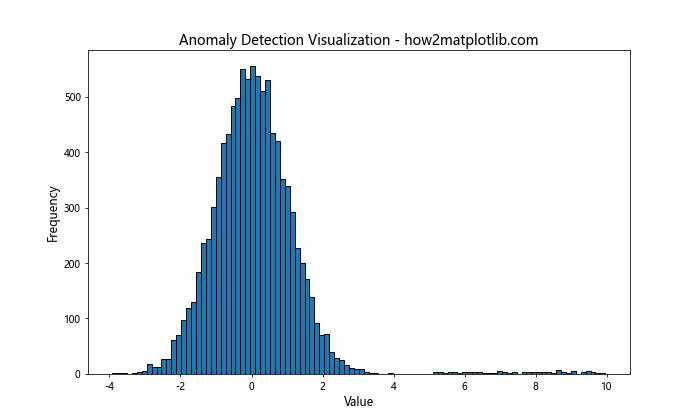
使用100个箱子可以更好地展示异常值的存在，而不会将它们淹没在主要分布中。

9. 动态调整箱宽

在某些情况下，我们可能需要动态调整箱宽以找到最佳的可视化效果。Matplotlib提供了交互式工具来实现这一点：

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.widgets import Slider

# 生成数据
np.random.seed(42)
data = np.random.gamma(shape=2, scale=2, size=10000)

# 创建图形和子图
fig, ax = plt.subplots(figsize=(10, 8))
plt.subplots_adjust(bottom=0.25)

# 初始箱子数量
initial_bins = 50

# 绘制初始直方图
n, bins, patches = ax.hist(data, bins=initial_bins, edgecolor='black')

# 创建滑块轴
ax_slider = plt.axes([0.2, 0.1, 0.6, 0.03])
slider = Slider(ax_slider, 'Bins', 10, 200, valinit=initial_bins, valstep=1)

# 更新函数
def update(val):
    ax.clear()
    ax.hist(data, bins=int(slider.val), edgecolor='black')
    ax.set_title('Dynamic Bin Size Adjustment - how2matplotlib.com', fontsize=14)
    ax.set_xlabel('Value', fontsize=12)
    ax.set_ylabel('Frequency', fontsize=12)
    fig.canvas.draw_idle()

# 连接滑块到更新函数
slider.on_changed(update)

# 设置初始标题和标签
ax.set_title('Dynamic Bin Size Adjustment - how2matplotlib.com', fontsize=14)
ax.set_xlabel('Value', fontsize=12)
ax.set_ylabel('Frequency', fontsize=12)

# 显示图形
plt.show()

Output:

Matplotlib直方图中的箱宽设置：全面指南与实践

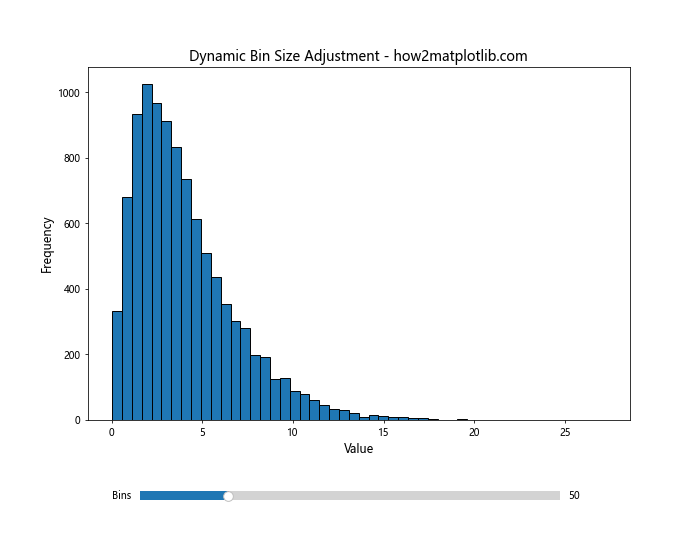
这个交互式工具允许用户实时调整箱子的数量，从而找到最适合数据的箱宽设置。

10. 结论

选择合适的箱宽是绘制直方图时的一个关键步骤。它不仅影响图形的视觉效果，还会影响我们对数据的解释。通过本文的探讨，我们了解到：

  1. 箱宽的选择需要考虑数据的分布特征、样本大小和可视化目标。
  2. Matplotlib提供了多种设置箱宽的方法，包括直接指定箱子数量、设置箱宽、使用预定义的字符串参数等。
  3. 自动选择算法如Sturges规则、Freedman-Diaconis规则和Scott规则可以帮助我们快速找到合适的箱宽。
  4. 对于不同类型的数据分布（如正态分布、偏斜分布、多峰分布），可能需要不同的箱宽设置策略。
  5. 样本大小也是影响箱宽选择的一个重要因素，大样本通常可以使用更多的箱子。
  6. 在实际应用中，可能需要尝试不同的箱宽设置，甚至使用交互式工具来找到最佳的可视化效果。

总之，选择合适的箱宽是一个需要平衡艺术和科学的过程。通过理解数据特征、考虑可视化目标，并灵活运用Matplotlib提供的各种工具，我们可以创建既美观又富有洞察力的直方图。

Camera课程

Camera API2 教程

API2 教程
Camera 性能教程

Perf 教程
Camera Native Framework 教程

Native FW 教程
Camera QCOM ISP 教程

ISP 教程
Camera QCOM Sensor 教程

Sensor 教程

Python教程

Python 教程

Python 教程
NumPy 教程

NumPy 教程
Django 教程

Django 教程

Java教程

Java 教程

Java 教程

Web教程

JavaScript 教程

JavaScript 教程
jQuery 教程

jQuery 教程
CSS 教程

CSS 教程
PHP 教程

PHP 教程
Laravel 教程

Laravel 教程
TypeScript 教程

TypeScript 教程
WordPress 教程

WordPress 教程

数据库教程

SQL 教程

SQL 教程
SQLite 教程

SQLite 教程
MySQL 教程

MySQL 教程
PL/SQL 教程

PL/SQL 教程
MongoDB 教程

MongoDB 教程

图形图像教程

OpenCV 教程

OpenCV 教程

办公软件教程

Excel 教程

Excel 教程

Linux教程

Linux命令全集

Linux命令全集
Linux内核API

Linux内核API
LVGL 教程

LVGL 教程

计算机教程

操作系统 教程

操作系统 教程
计算机网络 教程

计算机网络 教程
C语言 教程

C语言 教程
C++ 教程

C++ 教程
Swift 教程

Swift 教程

大数据教程

Hadoop 教程

Hadoop 教程
Spark 教程

Spark 教程
Scala 教程

Scala 教程

开发工具教程

Git 教程

Git 教程
Jenkins 教程

Jenkins 教程
ChatGPT 教程

ChatGPT 教程
IntelliJ 教程

IntelliJ 教程